广东省深圳市重点中学2023-2024学年八年级上学期期中考试数学试卷
试卷更新日期:2023-11-06 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 4的平方根是( )A、2 B、﹣2 C、16 D、±22. 下列运算错误的是( )A、=2 B、 C、=2 D、3. 下列线段能组成直角三角形的一组是( )A、1,2,2 B、3,4,5 C、 ,2, D、5,6,74. 点A(3,4)关于x轴的对称点的坐标是( )A、(3,-4) B、(-3,4) C、(-3,-4) D、(-4,3)5. 点P的坐标为(2﹣a,3a+6),且到两坐标轴的距离相等,则点P的坐标为( )A、(3,3) B、(3,﹣3) C、(6,﹣6) D、(3,3)或(6,﹣6)6. 一个正方形的面积为29,则它的边长应在( )A、3到4之间 B、4到5之间 C、5到6之间 D、6到7之间7. 如图为正比例函数y=kx(k≠0)的图象,则一次函数y=x+k的大致图象是( )
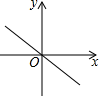 A、
A、 B、
B、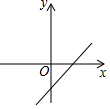 C、
C、 D、
D、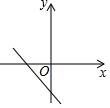 8. 已知M(-3,y1),N(2,y2)是直线y=-3x+1上的两个点,则y1、y2的大小关系是( )A、y1<y2 B、y1>y2 C、y1≥y2 D、y1=y29. 小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家,下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系( )A、
8. 已知M(-3,y1),N(2,y2)是直线y=-3x+1上的两个点,则y1、y2的大小关系是( )A、y1<y2 B、y1>y2 C、y1≥y2 D、y1=y29. 小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家,下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系( )A、 B、
B、 C、
C、 D、
D、 10. 在平面直角坐标系中,已知一次函数y=-x+6与x , y轴分别交于A , B两点,点C(0,n)是线段BO上一点,将△ACB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )
10. 在平面直角坐标系中,已知一次函数y=-x+6与x , y轴分别交于A , B两点,点C(0,n)是线段BO上一点,将△ACB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )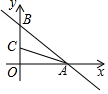 A、(0,3) B、(0,) C、(0,) D、(0,)
A、(0,3) B、(0,) C、(0,) D、(0,)二、填空题(每题3分,共15分)
-
11. 某班级第4组第5排的位置可以用有序数对(4,5)表示,则第3组第1排的位置可用有序数对 来表示.12. 在Rt△ABC中,∠C=90°,AB=25cm , AC=15cm , CH⊥AB , 垂足为H , CH= .
 13. 如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为 .
13. 如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为 . 14. 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为 .
14. 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为 . 15. 如图,圆柱形玻璃杯高为12cm、底面周长为18cm , 在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为cm .
15. 如图,圆柱形玻璃杯高为12cm、底面周长为18cm , 在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为cm .
三、解答题(共55分)
-
16. 计算:(1)、;(2)、;(3)、17. 设的小数部分为a , 的小数部分为b , 求(a-1)(b+2)的值.18. 如图一次函数y=kx+b的图象经过点A和点B .
 (1)、写出点A和点B的坐标并求出k、b的值;(2)、求出当x=时的函数值.19. 在平面直角坐标系中,△ABC各顶点坐标分别为:A(4,0),B(-1,4),C(-3,1).
(1)、写出点A和点B的坐标并求出k、b的值;(2)、求出当x=时的函数值.19. 在平面直角坐标系中,△ABC各顶点坐标分别为:A(4,0),B(-1,4),C(-3,1).
⑴在图中作△A'B'C',使△A'B'C′和△ABC关于x轴对称;
⑵已知△A1B1C1与△ABC关于y轴对称,写出点A1 , B1 , C1的坐标;
⑶求△ABC的面积.
20. 如图所示,折叠长方形一边AD , 点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,求BF与FC的长. 21. 阅读下列材料,然后解答下列问题:在进行代数式化简时,我们有时会碰上如 , 这样的式子,其实我们还可以将其进一步化简:
21. 阅读下列材料,然后解答下列问题:在进行代数式化简时,我们有时会碰上如 , 这样的式子,其实我们还可以将其进一步化简:(一);
(二);
(三) . 以上这种化简的方法叫分母有理化.
(1)、请用不同的方法化简;①参照(二)式化简= ▲ .
②参照(三)式化简= ▲ .
(请写出计算过程)
(2)、化简: .22. 如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A , 交x轴于点B(3,0),点P是直线AB上方第一象限内的动点. (1)、求直线AB的表达式和点A的坐标;(2)、点P是直线x=2上一动点,当△ABP的面积与△ABO的面积相等时,求点P的坐标;(3)、当△ABP为等腰直角三角形时,请直接写出点P的坐标.
(1)、求直线AB的表达式和点A的坐标;(2)、点P是直线x=2上一动点,当△ABP的面积与△ABO的面积相等时,求点P的坐标;(3)、当△ABP为等腰直角三角形时,请直接写出点P的坐标.