【北师大版·数学】2024年中考一轮复习之二次函数的实际应用-几何问题
试卷更新日期:2023-11-05 类型:一轮复习
一、选择题
-
1. 已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y= 的图象可能是( )
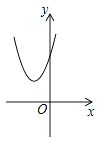 A、
A、 B、
B、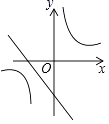 C、
C、 D、
D、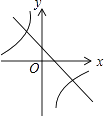 2. 如图1,在平行四边形中, , 已知点在边上,以1m/s的速度从点向点运动,点在边上,以的速度从点向点运动.若点 , 同时出发,当点到达点时,点恰好到达点处,此时两点都停止运动.图2是的面积与点的运动时间之间的函数关系图象(点为图象的最高点),则平行四边形的面积为( )
2. 如图1,在平行四边形中, , 已知点在边上,以1m/s的速度从点向点运动,点在边上,以的速度从点向点运动.若点 , 同时出发,当点到达点时,点恰好到达点处,此时两点都停止运动.图2是的面积与点的运动时间之间的函数关系图象(点为图象的最高点),则平行四边形的面积为( )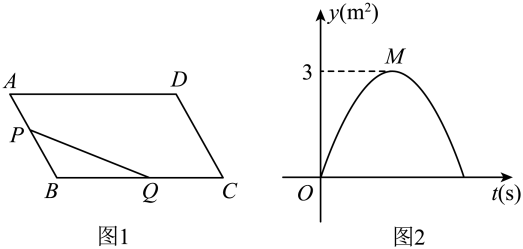 A、 B、 C、 D、3. 如图1,在矩形中,对角线与相交于点、动点从点出发,在线段上匀速运动,到达点时停止设点运动的路程为 , 线段的长为 , 如果与的函数图象如图所示,则矩形的面积是( )
A、 B、 C、 D、3. 如图1,在矩形中,对角线与相交于点、动点从点出发,在线段上匀速运动,到达点时停止设点运动的路程为 , 线段的长为 , 如果与的函数图象如图所示,则矩形的面积是( ) A、60 B、48 C、24 D、124. 如图,在中, , , . 动点在线段上从顶点出发以每秒1个单位的速度向终点点运动,动点在线段上从顶点出发以每秒2个单位的速度向终点运动,两点同时出发,有一点到达终点后两点都停止运动.设运动的时间为秒,的面积为 , 则关于的函数图象大致是
A、60 B、48 C、24 D、124. 如图,在中, , , . 动点在线段上从顶点出发以每秒1个单位的速度向终点点运动,动点在线段上从顶点出发以每秒2个单位的速度向终点运动,两点同时出发,有一点到达终点后两点都停止运动.设运动的时间为秒,的面积为 , 则关于的函数图象大致是 A、
A、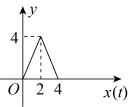 B、
B、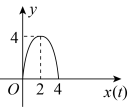 C、
C、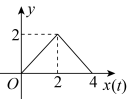 D、
D、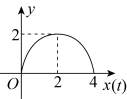 5. 如图,在中,对角线相交于点O, , 若过点O且与边分别相交于点E,F,设 , 则y关于x的函数图象大致为( )
5. 如图,在中,对角线相交于点O, , 若过点O且与边分别相交于点E,F,设 , 则y关于x的函数图象大致为( )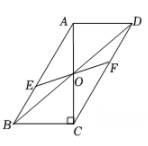 A、
A、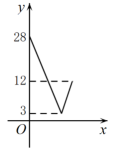 B、
B、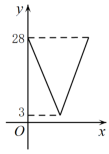 C、
C、 D、
D、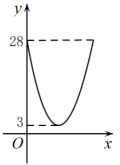 6. 已知,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个.顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( )
6. 已知,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个.顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( ) A、6 B、7 C、8 D、97. 有一个矩形苗圃园,其中一边靠墙,另外三边用长为的篱笆围成.已知墙长为若平行于墙的一边长不小于则这个苗圃园面积的最大值和最小值分别为( )
A、6 B、7 C、8 D、97. 有一个矩形苗圃园,其中一边靠墙,另外三边用长为的篱笆围成.已知墙长为若平行于墙的一边长不小于则这个苗圃园面积的最大值和最小值分别为( ) A、 B、 C、 D、8. 抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.有下列结论:①关于x的方程﹣x2+2x+m+1(m为常数)=0有两个不相等的实数根;②﹣1<m<2;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为 . 其中正确的个数是( )A、1 B、2 C、3 D、49. 如图,矩形ABCD各边中点分别是E、F、G、H,AB=2 ,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是( )
A、 B、 C、 D、8. 抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.有下列结论:①关于x的方程﹣x2+2x+m+1(m为常数)=0有两个不相等的实数根;②﹣1<m<2;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为 . 其中正确的个数是( )A、1 B、2 C、3 D、49. 如图,矩形ABCD各边中点分别是E、F、G、H,AB=2 ,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,线段 ,点 、 在 上, .已知点 从点 出发,以每秒1个单位长度的速度沿着 向点 移动,到达点 后停止移动,在点 移动过程中作如下操作:先以点 为圆心, 、 的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面.设点 的移动时间为(秒).两个圆锥的底面面积之和为 .则 关于 的函数图象大致是( )
10. 如图,线段 ,点 、 在 上, .已知点 从点 出发,以每秒1个单位长度的速度沿着 向点 移动,到达点 后停止移动,在点 移动过程中作如下操作:先以点 为圆心, 、 的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面.设点 的移动时间为(秒).两个圆锥的底面面积之和为 .则 关于 的函数图象大致是( )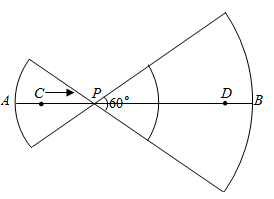 A、
A、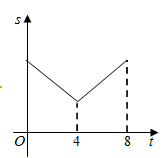 B、
B、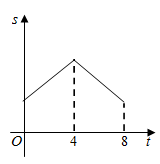 C、
C、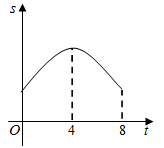 D、
D、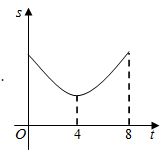
二、填空题
-
11. 已知抛物线y=x2-k的顶点为P,与x轴交于点A,B,且△ABP是正三角形,则k的值是12. 如图,王叔叔想用长为的栅栏,再借助房屋的外墙围成一个矩形羊圈 , 已知房屋外墙足够长,当矩形的边 时,羊圈的面积最大.
 13. 某品牌水果冻的高为3cm,底面圆的直径为4cm,两个水果冻倒装在一个长方体盒子内,如图为横断示意图,水果冻的截面可以近似地看成两条抛物线.以左侧抛物线的顶点O为原点,建立如图所示的直角坐标系.
13. 某品牌水果冻的高为3cm,底面圆的直径为4cm,两个水果冻倒装在一个长方体盒子内,如图为横断示意图,水果冻的截面可以近似地看成两条抛物线.以左侧抛物线的顶点O为原点,建立如图所示的直角坐标系.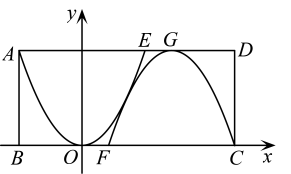 (1)、以O为顶点的抛物线的函数表达式是 .(2)、制作该长方体盒子所需纸张面积最小值是cm2 . (不计重叠部分)14. 如图,中, , , 为中点.、是边、上的动点,从出发向运动,同时以相同的速度从出发向运动,运动到停止.当为时,的面积最大.
(1)、以O为顶点的抛物线的函数表达式是 .(2)、制作该长方体盒子所需纸张面积最小值是cm2 . (不计重叠部分)14. 如图,中, , , 为中点.、是边、上的动点,从出发向运动,同时以相同的速度从出发向运动,运动到停止.当为时,的面积最大. 15. 如图,P是抛物线y=x2-x-4在第四象限的一点,过点P分别向x轴和y轴作垂线,垂足分别为A、B,则四边形OAPB周长的最大值为 .
15. 如图,P是抛物线y=x2-x-4在第四象限的一点,过点P分别向x轴和y轴作垂线,垂足分别为A、B,则四边形OAPB周长的最大值为 .
三、解答题
-
16. 根据以下素材,探索完成任务.
如何设计跳长绳方案
素材1
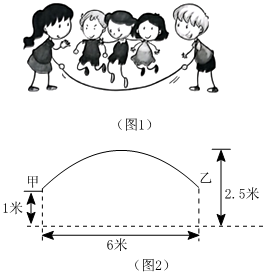
图1是集体跳长绳比赛,比赛时,各队跳绳10人,摇绳2人,共计12人图2是绳甩到最高处时的示意图,可以近似的看作一条抛物线,正在甩绳的甲、乙两位队员拿绳的手间距6米,到地面的距离均为1米,绳子最高点距离地面2.5米.
素材2
某队跳绳成员有6名男生和4名女生,男生身高1.70米至1.80米,女生身高1.66米至1.69米跳长绳比赛时,可以采用一路纵队或两路纵队并排的方式安排队员位置,但为了保证安全,人与人之间距离至少0.5米
问题解决
任务1
确定长绳形状
在图2中建立合适的直角坐标系,并求出抛物线的函数表达式
任务2
探究站队方式
当该队以一路纵队的方式跳绳时,绳子能否顺利的甩过所有队员的头顶?
任务3
拟定位置方案
为了更顺利的完成跳绳,现按中间高两边低的方式居中安排站位请在你所建立的坐标系中,求出左边第一位跳绳队员横坐标的最大取值范围.
17. 根据以下素材,探索完成任务.如何调整蔬菜大棚的结构?
素材1
我国的大棚如图种植技术已十分成熟,一块土地上有一个蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在墙体OA上,另一端固定在墙体BC上,其横截面有2根支架DE,FG,相关数据如图2所示,其中支架 ,

素材2
已知大棚共有支架400根,为增加棚内空间,拟将图2中棚顶向上调整,支架总数不变,对应支架的长度变化如图3所示,调整后C与E上升相同的高度,增加的支架单价为60元/米接口忽略不计 , 现有改造经费32000元.

问题解决
任务1
确定大棚形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
尝试改造方案
当米,只考虑经费情况下,请通过计算说明能否完成改造.
任务3
拟定最优方案
只考虑经费情况下,求出的最大值.
18. 某农场要建一个矩形养鸡场,鸡场的一边靠墙,另外三边用木栅栏围成.已知墙长25m,木栅栏长47m,在与墙垂直的一边留出1m宽的出入口(另选材料建出入门).求鸡场面积的最大值.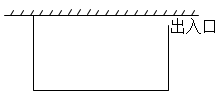 19. 如图,一个边长为 的正方形花坛是由4块全等的小正方形区域组成的中心对称图形.在小正方形 中,点G、E、F分别在 、 、 上,且 .在 、 、五边形 三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元.问:点E在什么位置时,正方形花坛种植花卉所需的总费用最少,最少为多少元?
19. 如图,一个边长为 的正方形花坛是由4块全等的小正方形区域组成的中心对称图形.在小正方形 中,点G、E、F分别在 、 、 上,且 .在 、 、五边形 三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元.问:点E在什么位置时,正方形花坛种植花卉所需的总费用最少,最少为多少元? 20. 如图,正方形ABCD中,AB=12,AE= AB , 点P在BC上运动(不与B , C重合),过点P作PQ⊥EP , 交CD于点Q , 求在点P运动的过程中,BP多长时,CQ有最大值,并求出最大值.
20. 如图,正方形ABCD中,AB=12,AE= AB , 点P在BC上运动(不与B , C重合),过点P作PQ⊥EP , 交CD于点Q , 求在点P运动的过程中,BP多长时,CQ有最大值,并求出最大值.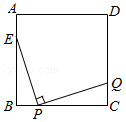
四、综合题
-
21. 某建筑物的窗户如图所示,上半部分是等腰三角形, , , 点、、分别是边、、的中点;下半部分四边形是矩形, , 制造窗户框的材料总长为16米(图中所有黑线的长度和),设米,米.
 (1)、求与之间的函数关系式,并求出自变量的取值范围;(2)、当为多少时,窗户透过的光线最多(窗户的面积最大),并计算窗户的最大面积.22. 如图,抛物线与轴交于 , 两点,与轴交于点 . 已知点的坐标是 , 抛物线的对称轴是直线 .
(1)、求与之间的函数关系式,并求出自变量的取值范围;(2)、当为多少时,窗户透过的光线最多(窗户的面积最大),并计算窗户的最大面积.22. 如图,抛物线与轴交于 , 两点,与轴交于点 . 已知点的坐标是 , 抛物线的对称轴是直线 . (1)、直接写出点的坐标;(2)、在对称轴上找一点 , 使的值最小.求点的坐标和的最小值;(3)、第一象限内的抛物线上有一动点 , 过点作轴,垂足为 , 连接交于点 . 依题意补全图形,当的值最大时,求点的坐标.23. 太原的五月是月季的狂欢,滨河路上月季花扮靓道路两侧,形成了“绿染龙城,花满并州”的景观效果.市林业局将如图所示的一块长80米,宽40米的矩形空地分成五块小矩形区域,建成月季花种植基地.一块正方形区域为育苗区,一块矩形区域为存储区,其它区域分别种植风花月季,藤本月季和树桩月季.已知存储区的一边与育苗区的宽相等,另一边长为20米,风花月季、藤本月季和树桩月季每年每平方米的产值分别为200元、300元和400元.
(1)、直接写出点的坐标;(2)、在对称轴上找一点 , 使的值最小.求点的坐标和的最小值;(3)、第一象限内的抛物线上有一动点 , 过点作轴,垂足为 , 连接交于点 . 依题意补全图形,当的值最大时,求点的坐标.23. 太原的五月是月季的狂欢,滨河路上月季花扮靓道路两侧,形成了“绿染龙城,花满并州”的景观效果.市林业局将如图所示的一块长80米,宽40米的矩形空地分成五块小矩形区域,建成月季花种植基地.一块正方形区域为育苗区,一块矩形区域为存储区,其它区域分别种植风花月季,藤本月季和树桩月季.已知存储区的一边与育苗区的宽相等,另一边长为20米,风花月季、藤本月季和树桩月季每年每平方米的产值分别为200元、300元和400元.
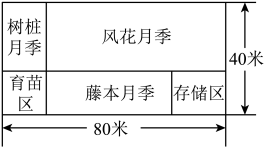 (1)、如果风花月季与藤本月季每年的产值相等,求育苗区的边长;(2)、如果风花月季种植面积与育苗区面积的差不超过2120平方米,求这三种月季花每年总产值的最大值.24. 根据以下素材,探索完成任务.
(1)、如果风花月季与藤本月季每年的产值相等,求育苗区的边长;(2)、如果风花月季种植面积与育苗区面积的差不超过2120平方米,求这三种月季花每年总产值的最大值.24. 根据以下素材,探索完成任务.如何设计跳长绳方案
素材1
图1是集体跳长绳比赛,比赛时,各队跳绳10人,摇绳2人,共计12人.图2是绳甩到最高处时的示意图,可以近似的看作一条抛物线,正在甩绳的甲、乙两位队员拿绳的手间距6米,到地面的距离均为1米,绳子最高点距离地面2.5米.
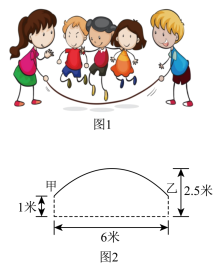
素材2
某队跳绳成员有6名男生和4名女生,男生身高1.70米至1.80米,女生身高1.66米至1.68米.跳长绳比赛时,可以采用一路纵队或两路纵队并排的方式安排队员位置,但为了保证安全,人与人之间距离至少0.5米.
问题解决
任务1
确定长绳形状
在图2中建立合适的直角坐标系,并求出抛物线的函数表达式.
任务2
探究站队方式
当该队以一路纵队的方式跳绳时,绳子能否顺利的甩过所有队员的头顶?
任务3
拟定位置方案
为了更顺利的完成跳绳,现按中间高两边低的方式居中安排站位.请在你所建立的坐标系中,求出左边第一位跳绳队员横坐标的最大取值范围.
25. 如图所示,取某一位置的水平线为轴,建立了平面坐标系后,小山坡可以近似看成抛物线 . 小明在离点的楼顶抛出一球,其运动轨迹为抛物线 , 落在山坡的点处,测得点离轴的距离为 . (1)、求点的坐标.(2)、求小球飞行过程中,离山坡的最大高度.
(1)、求点的坐标.(2)、求小球飞行过程中,离山坡的最大高度.