【北师大版·数学】2024年中考一轮复习之直角三角形的性质
试卷更新日期:2023-11-05 类型:一轮复习
一、选择题
-
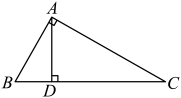
1. 如图,在 中, , ,AD是斜边BC上的中线,将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于( )
 A、120° B、108° C、72° D、36°2. 如图,在△ABC中,∠ACB=90°, ∠A=39° ,以点C为圆心,CB长为半径作弧交AB于点D,B为圆心,大于 , 两弧相交于点E,作射线CE交AB于点F, 求∠BCF的度数 ( )
A、120° B、108° C、72° D、36°2. 如图,在△ABC中,∠ACB=90°, ∠A=39° ,以点C为圆心,CB长为半径作弧交AB于点D,B为圆心,大于 , 两弧相交于点E,作射线CE交AB于点F, 求∠BCF的度数 ( ) A、38° B、39° C、40° D、51°3. 如图,是的直径,D,C是上的点, , 则的度数是( )
A、38° B、39° C、40° D、51°3. 如图,是的直径,D,C是上的点, , 则的度数是( ) A、 B、 C、 D、4. 如图,在中, , , . 点F是中点,连接 , 把线段沿射线方向平移到 , 点D在上.则线段在平移过程中扫过区域形成的四边形的周长和面积分别是( )
A、 B、 C、 D、4. 如图,在中, , , . 点F是中点,连接 , 把线段沿射线方向平移到 , 点D在上.则线段在平移过程中扫过区域形成的四边形的周长和面积分别是( ) A、16,6 B、18,18 C、16,12 D、12,165. 如图,四边形内接于为对角线,经过圆心 . 若 , 则的度数为( )
A、16,6 B、18,18 C、16,12 D、12,165. 如图,四边形内接于为对角线,经过圆心 . 若 , 则的度数为( )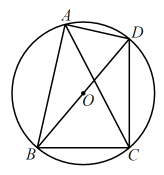 A、 B、 C、 D、6. 矩形和直角三角形的位置如图所示,点在EG上,点在EF上.若 , 则等于( )
A、 B、 C、 D、6. 矩形和直角三角形的位置如图所示,点在EG上,点在EF上.若 , 则等于( ) A、 B、 C、 D、7. 一块直角三角板和一把直尺如图摆放,直尺的一边经过三角板的顶点 , 若 , 则的度数为( )
A、 B、 C、 D、7. 一块直角三角板和一把直尺如图摆放,直尺的一边经过三角板的顶点 , 若 , 则的度数为( ) A、 B、 C、 D、8. 如图,是的切线, , 则( )
A、 B、 C、 D、8. 如图,是的切线, , 则( ) A、 B、 C、 D、9. 如图,将一块含有45°角的直角三角板放置在两条平行线上,若∠1=25°,则∠2为( )
A、 B、 C、 D、9. 如图,将一块含有45°角的直角三角板放置在两条平行线上,若∠1=25°,则∠2为( ) A、15° B、20° C、25° D、30°10. 如图,AB是圆O的直径,C,D是AB上的两点,连接AC,BD相交于点E,若∠BEC=56°,那么∠DOC的度数为( )
A、15° B、20° C、25° D、30°10. 如图,AB是圆O的直径,C,D是AB上的两点,连接AC,BD相交于点E,若∠BEC=56°,那么∠DOC的度数为( ) A、28° B、56° C、64° D、68°
A、28° B、56° C、64° D、68°二、填空题
-
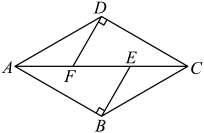
11. 如图,菱形中, , , , 垂足分别为 , , 若 , 则 .
 12. 如图所示是地球截面图,其中 , 分别表示南回归线和北回归线,表示赤道,点表示太原市的位置.现已知地球南回归线的纬度是南纬 , 太原市的纬度是北纬 , 而冬至正午时,太阳光直射南回归线(光线的延长线经过地心),则太原市冬至正午时,太阳光线与地面水平线的夹角的度数是 .
12. 如图所示是地球截面图,其中 , 分别表示南回归线和北回归线,表示赤道,点表示太原市的位置.现已知地球南回归线的纬度是南纬 , 太原市的纬度是北纬 , 而冬至正午时,太阳光直射南回归线(光线的延长线经过地心),则太原市冬至正午时,太阳光线与地面水平线的夹角的度数是 .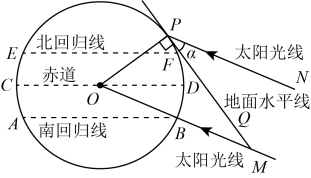 13. 如图,在中,是上的高,E是边的中点,连接 , 若 , , 则 .
13. 如图,在中,是上的高,E是边的中点,连接 , 若 , , 则 . 14. 如图,在建高铁的某段路基横断面为梯形ABCD,DC∥AB.BC长6米,坡角β为45°,AD的坡角α为30°,则AD长为米 (结果保留根号).
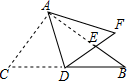
14. 如图,在建高铁的某段路基横断面为梯形ABCD,DC∥AB.BC长6米,坡角β为45°,AD的坡角α为30°,则AD长为米 (结果保留根号). 15. 如图,在中, , , , 把沿翻折得到 , 过点B作 , 交于点E,点F是线段上一点,且 . 则下列结论中:①;②;③;④ . 正确的有(把所有正确答案的序号都填上)
15. 如图,在中, , , , 把沿翻折得到 , 过点B作 , 交于点E,点F是线段上一点,且 . 则下列结论中:①;②;③;④ . 正确的有(把所有正确答案的序号都填上)
三、作图题
-
16. 图、图、图均是的正方形网格,每个小正方形的边长均为 , 点 , , , 均在格点上,用无刻度的直尺在给定的网格中按要求画图:
 (1)、如图 , 在上画一点 , 连结 , 使;
(1)、如图 , 在上画一点 , 连结 , 使;
(2)、如图 , 在上画一点 , 连结 , 使;
(3)、如图 , 在上画一点 , 连结 , , 使 .17. 如图,已知 , . (1)、尺规作图:作 , 垂足为保留作图痕迹,不写作法;(2)、求证: .18. 如图①、图②均是的正方形网格,每个小正方形的边长均为1,的顶点均在格点上,用无刻度的直尺在给定的网格中按要求画图.
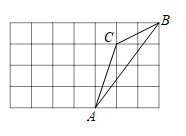
(1)、尺规作图:作 , 垂足为保留作图痕迹,不写作法;(2)、求证: .18. 如图①、图②均是的正方形网格,每个小正方形的边长均为1,的顶点均在格点上,用无刻度的直尺在给定的网格中按要求画图. (1)、在图①中的线段BC上找一点E , 连接AE , 使为等腰三角形.(2)、在图②中的线段AD上找一点F , 连接BF , 使为直角三角形.19. 如图,在每个小正方形的边长为1的网格中, 的顶点A,B,C均落在格点上.
(1)、在图①中的线段BC上找一点E , 连接AE , 使为等腰三角形.(2)、在图②中的线段AD上找一点F , 连接BF , 使为直角三角形.19. 如图,在每个小正方形的边长为1的网格中, 的顶点A,B,C均落在格点上.①线段 的长等于 ▲ ;
②在射线 上有两点P,Q,满足 且 ,请用无刻度的直尺,在如图所示的网格中,画出点P,点Q,并简要说明点P,点Q的位置是如何找到的(不要求证明).
四、解答题
-
20. 如图,四边形是平行四边形,对角线、相交于点 , 点、分别在、上, , 连接 , 且 .
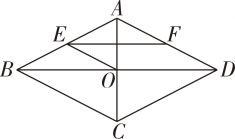 (1)、求证:四边形是菱形;
(1)、求证:四边形是菱形;
(2)、连接 , 若点是的中点, , , 求四边形的面积.21. 如图,某海域有一小岛P,一艘轮船在A处测得小岛P位于北偏东60°的方向上,当轮船自西向东航行12海里到达B处,在B处测得小岛P位于北偏东30°方向上,若以点P为圆心,半径为10海里的圆形海域内有暗礁,那么轮船由B处继续向东航行是否有触礁危险?请说明理由.(参考数据:). 22. 享有“安徽第一楼”之称的安徽省国际金融大厦,它由高度不同的两座楼组成,如图,从左楼顶C处测得右楼楼顶A处的仰角为60°,在左楼楼底D处测得A处的仰角为75°,已知左楼CD高126米,请你利用已知数据估算右楼AB的高.(结果精确到1米,≈1.7)
22. 享有“安徽第一楼”之称的安徽省国际金融大厦,它由高度不同的两座楼组成,如图,从左楼顶C处测得右楼楼顶A处的仰角为60°,在左楼楼底D处测得A处的仰角为75°,已知左楼CD高126米,请你利用已知数据估算右楼AB的高.(结果精确到1米,≈1.7)

五、综合题