【北师大版·数学】2024年中考一轮复习之圆周角定理
试卷更新日期:2023-11-05 类型:一轮复习
一、选择题
-
1. 如图,在Rt△ACB中,∠ACB=90°,AC=6,BC=8,若以AC为直径的⊙O交AB于点D,则CD的长为( )
 A、 B、 C、 D、52. 如图,⊙o是△ABC的外接圆,CD是⊙O的直径,∠B=35°,则∠ACD的度数为 ( )
A、 B、 C、 D、52. 如图,⊙o是△ABC的外接圆,CD是⊙O的直径,∠B=35°,则∠ACD的度数为 ( ) A、45° B、50° C、55° D、60°3. 如图,菱形ABCD的两边与⊙O分别相切于点A、C,点D在⊙O上,则∠B的度数是( )
A、45° B、50° C、55° D、60°3. 如图,菱形ABCD的两边与⊙O分别相切于点A、C,点D在⊙O上,则∠B的度数是( ) A、45° B、50° C、60° D、65°4. 如图,AB是⊙O的直径,C、D是圆上的点,若∠D=20°,则 ∠BAC的值( )
A、45° B、50° C、60° D、65°4. 如图,AB是⊙O的直径,C、D是圆上的点,若∠D=20°,则 ∠BAC的值( )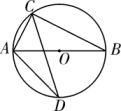 A、20° B、60° C、70° D、80°5. 如图, AB是⊙O的直径, C, D是⊙O上AB两侧的点,若∠D=30°,则tan ∠ABC的值为( )
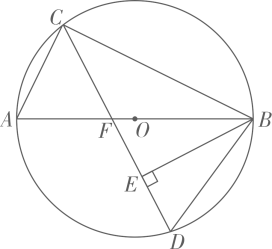
A、20° B、60° C、70° D、80°5. 如图, AB是⊙O的直径, C, D是⊙O上AB两侧的点,若∠D=30°,则tan ∠ABC的值为( ) A、 B、 C、 D、6. 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为( )
A、 B、 C、 D、6. 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为( )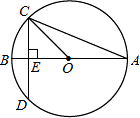 A、2 B、4 C、4 D、87. 如图,AB为⊙O的直径,点C在⊙O上,且 , 点D在上(不与点B、点C重合),则∠BDC的大小为( )
A、2 B、4 C、4 D、87. 如图,AB为⊙O的直径,点C在⊙O上,且 , 点D在上(不与点B、点C重合),则∠BDC的大小为( )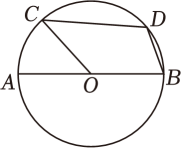 A、110° B、112.5° C、115° D、120°8. 如图,四边形是的内接四边形, , 则的度数是( )
A、110° B、112.5° C、115° D、120°8. 如图,四边形是的内接四边形, , 则的度数是( )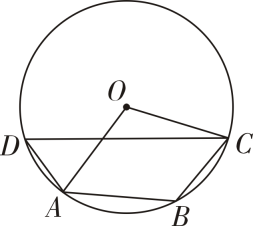 A、
A、
B、
C、
D、9. 如图,是的直径,、是上的两点,若 , 则的度数为( )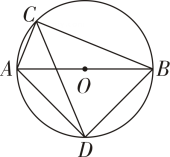 A、 B、 C、 D、10. 如图,在中, , 是劣弧的中点,是优弧任意一点,连接 , , 则的度数是( )
A、 B、 C、 D、10. 如图,在中, , 是劣弧的中点,是优弧任意一点,连接 , , 则的度数是( ) A、或
A、或
B、
C、
D、二、填空题
-
11. 如图,直线与半径为的相切于点 , 点在上,连接、 , 且 , 弦 , 则的长为 .
 12. 如图,在中,为直径,点是上的一点,连接、 , 以为圆心,的长为半径作弧,恰好经过点 , 若 , 则图中阴影部分的周长是 结果保留根号和 .
12. 如图,在中,为直径,点是上的一点,连接、 , 以为圆心,的长为半径作弧,恰好经过点 , 若 , 则图中阴影部分的周长是 结果保留根号和 . 13. 如图,是的直径,是弦,于点 , 于点若 , , 则的长是 .
13. 如图,是的直径,是弦,于点 , 于点若 , , 则的长是 .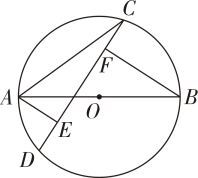 14. 如图,的弦 , 相交于点若 , , 则
14. 如图,的弦 , 相交于点若 , , 则 15. 如图,正方形ABCD的边长为3,点E , F分别在BC , CD上,且 , 连接AE , BF交于点P , 连接PD , 则的值为 .
15. 如图,正方形ABCD的边长为3,点E , F分别在BC , CD上,且 , 连接AE , BF交于点P , 连接PD , 则的值为 .
三、作图题
-
16. 已知:如图,∠MON=90°,△ABC中,∠C=90°,AC=3cm,BC=4cm,将△ABC的两个顶点A、B放在射线OM和ON上移动,作CD⊥ON于点D,记OA=x(当点O与A重合时,x的值为0),CD=y.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.
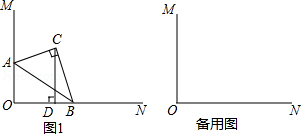 (1)、通过取点、画图、计算、测量等方法,得到了x与y的几组值,如下表(补全表格)
(1)、通过取点、画图、计算、测量等方法,得到了x与y的几组值,如下表(补全表格)x/cm
0
1
2
3
4
4.5
5
y/cm
2.4
3.0
3.5
3.9
4.0
3.9
(说明:补全表格时相关数值保留一位小数)
(2)、建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象. (3)、结合画出的函数图象,解决问题;当x的值为时,线段OC长度取得最大值为cm.17. 如图是的正方形网格,请仅用无刻度直尺完成下列画图问题,保留作图痕迹.
(3)、结合画出的函数图象,解决问题;当x的值为时,线段OC长度取得最大值为cm.17. 如图是的正方形网格,请仅用无刻度直尺完成下列画图问题,保留作图痕迹.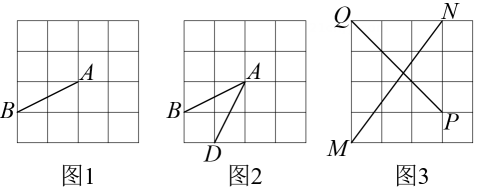 (1)、在图中,找一格点 , 连结 , 使画出一种即可 , 这样的格点与点不重合有 个
(1)、在图中,找一格点 , 连结 , 使画出一种即可 , 这样的格点与点不重合有 个
(2)、在图中,找一格点 , 连结、 , 使画出一种即可 .
(3)、在图中的线段上画一点 , 连结 , , 使 .18. 如图,在中, .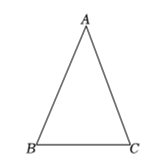 (1)、使用直尺和圆规,作交于点保留作图痕迹;(2)、以为圆心,的长为半径作弧,交于点 , 连接 , .
(1)、使用直尺和圆规,作交于点保留作图痕迹;(2)、以为圆心,的长为半径作弧,交于点 , 连接 , .
;
写出图中一个与相等的角 .19. 已知:点P是外一点. (1)、尺规作图:如图,过点P作出的两条切线 , , 切点分别为点E、点F.(保留作图痕迹,不要求写作法和证明)(2)、在(1)的条件下,若点D在上(点D不与E,F两点重合),且.求的度数.
(1)、尺规作图:如图,过点P作出的两条切线 , , 切点分别为点E、点F.(保留作图痕迹,不要求写作法和证明)(2)、在(1)的条件下,若点D在上(点D不与E,F两点重合),且.求的度数.四、解答题
-
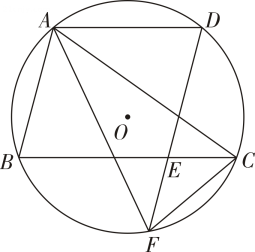
20. 如图,内接于 , 交于点 , 交于点 , 交于点 , 连接 , .
 (1)、求证:;
(1)、求证:;
(2)、若的半径为 , , 求的长结果保留 .21. 如图,四边形内接于 , 为的直径, . (1)、求的度数;(2)、若 , , 求的长度.22. 如图,四边形内接于 , 为的直径,过点作 , 交的延长线于点 , 交的延长线于点 , 连接若 .
(1)、求的度数;(2)、若 , , 求的长度.22. 如图,四边形内接于 , 为的直径,过点作 , 交的延长线于点 , 交的延长线于点 , 连接若 .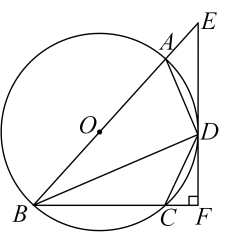 (1)、求证:为的切线.(2)、若 , , 求的半径.
(1)、求证:为的切线.(2)、若 , , 求的半径.五、综合题