【北师大版·数学】2024年中考一轮复习之切线的性质
试卷更新日期:2023-11-05 类型:一轮复习
一、选择题
-
1. 如图,、、是的切线,切点分别是、、若 , , 则的长是( )
 A、 B、 C、 D、2. 如图,分别与相切于A、B两点,连接 , 若 , 则的度数为( )
A、 B、 C、 D、2. 如图,分别与相切于A、B两点,连接 , 若 , 则的度数为( )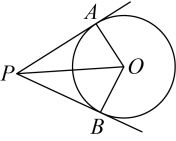 A、 B、 C、 D、3. 如图,在矩形中, , 以的中点为圆心,以长为半径画弧与相切于点 , 则阴影部分的面积为( )
A、 B、 C、 D、3. 如图,在矩形中, , 以的中点为圆心,以长为半径画弧与相切于点 , 则阴影部分的面积为( ) A、 B、 C、 D、4. 如图,、是的切线,切点分别是A、B,点E在上, , 那么等于( )
A、 B、 C、 D、4. 如图,、是的切线,切点分别是A、B,点E在上, , 那么等于( ) A、150° B、120° C、90° D、60°5. 如图,PA,PB是的切线,A、B为切点,若 , 则的度数为( )
A、150° B、120° C、90° D、60°5. 如图,PA,PB是的切线,A、B为切点,若 , 则的度数为( )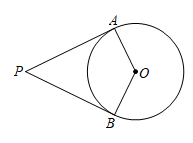 A、 B、 C、 D、6. 如图,AB是的切线,切点为点A,连接OB交于点C,过点A作交于点D,连接CD,若 , 则的度数为( )
A、 B、 C、 D、6. 如图,AB是的切线,切点为点A,连接OB交于点C,过点A作交于点D,连接CD,若 , 则的度数为( ) A、32° B、29° C、28° D、26°7. 如图,在中, , 是上的一点,以为直径的与相切于点 , 连接、 , 若 , , 则的长度是( )
A、32° B、29° C、28° D、26°7. 如图,在中, , 是上的一点,以为直径的与相切于点 , 连接、 , 若 , , 则的长度是( ) A、 B、 C、 D、8. 如图,与相切于点 , 与相交于点 , 若 , , 则的半径为( )
A、 B、 C、 D、8. 如图,与相切于点 , 与相交于点 , 若 , , 则的半径为( ) A、 B、 C、 D、9. 如图,是的直径,为上一点,过点的切线与的延长线交于点 , 若 , 则的度数是( )
A、 B、 C、 D、9. 如图,是的直径,为上一点,过点的切线与的延长线交于点 , 若 , 则的度数是( ) A、 B、 C、 D、10. 如图,在中, , 点在斜边上,以为直径的半圆与相切于点 , 与相交于点 , 连接 . 若 , , 则的长是( )
A、 B、 C、 D、10. 如图,在中, , 点在斜边上,以为直径的半圆与相切于点 , 与相交于点 , 连接 . 若 , , 则的长是( )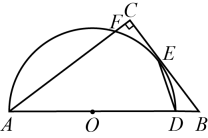 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,PA , PB分别与半径为3的⊙O相切于点A , B , 直线CD分别交PA , PB于点C , D , 并切⊙O于点E , 当PO=6时,△PCD的周长为 .
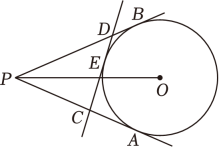 12. 如图,是的直径,是的切线,点B为切点,线段与交于点D . 点E是上的动点(不与点B、D重合).若 , 则的度数可能是 .
12. 如图,是的直径,是的切线,点B为切点,线段与交于点D . 点E是上的动点(不与点B、D重合).若 , 则的度数可能是 . 13. 把光盘、含60°角的三角板和直尺如图摆放,光盘与直尺和三角板的一边相切,若 , 则光盘的直径是 .
13. 把光盘、含60°角的三角板和直尺如图摆放,光盘与直尺和三角板的一边相切,若 , 则光盘的直径是 .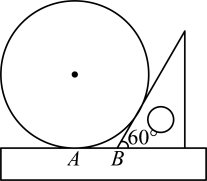 14. 如图,是的一条半径,点P是延长线上一点,过点P作的切线 , 点B为切点.若 , , 则 .
14. 如图,是的一条半径,点P是延长线上一点,过点P作的切线 , 点B为切点.若 , , 则 . 15. 如图,点O在边上,与边相切于点D,交边于点E,点F在弧上,连接 , , 则等于 .
15. 如图,点O在边上,与边相切于点D,交边于点E,点F在弧上,连接 , , 则等于 .
三、作图题
-
16. 在如图所示的网格中,每个小正方形的边长都为1,点A , B , C均为格点,且都在同一个圆上.
 (1)、AB的长度等于;(2)、请用无刻度的直尺在给定的网格中,画出圆的切线CD , 并简要说明点D的位置是如何找到的.
(1)、AB的长度等于;(2)、请用无刻度的直尺在给定的网格中,画出圆的切线CD , 并简要说明点D的位置是如何找到的..
17. 如图,△ABC是锐角三角形,请作⊙A,使它与BC相切于点M.(尺规作图,不写作法,保留作图痕迹) 18. 如图,点P是⊙O上一点,请用尺规过点P作⊙O的切线(不写画法,保留作图痕迹).
18. 如图,点P是⊙O上一点,请用尺规过点P作⊙O的切线(不写画法,保留作图痕迹).
四、解答题
-
19. 如图,是的弦,过点作 , 垂足为 , 过点作的切线,交的延长线于点 , 连接 .
 (1)、求证:;(2)、延长交于点 , 连接 , , 若 , , 求的长.20. 如图,在中, , 以为直径的与交于点D,过点B作 , 与过点C的的切线相交于点E.求证:.
(1)、求证:;(2)、延长交于点 , 连接 , , 若 , , 求的长.20. 如图,在中, , 以为直径的与交于点D,过点B作 , 与过点C的的切线相交于点E.求证:. 21. 如图, 为 的直径,点 在 上,且点C是 的中点,连接 ,过点C作 的切线 交射线 于点E. 连接 ,已知 , ,试求线段 的长.
21. 如图, 为 的直径,点 在 上,且点C是 的中点,连接 ,过点C作 的切线 交射线 于点E. 连接 ,已知 , ,试求线段 的长.
五、综合题
-
22. 如图,直线与相切于点C , 射线与交于点D , E , 连结 . 连结 .
 (1)、求证:;(2)、若 , , 求弧的长.23. 如图,是的直径,点在上, , 过点的切线与的延长线相交于点 , 与相交于点 .
(1)、求证:;(2)、若 , , 求弧的长.23. 如图,是的直径,点在上, , 过点的切线与的延长线相交于点 , 与相交于点 . (1)、求证:;(2)、若 , , 求的长.
(1)、求证:;(2)、若 , , 求的长.

