【北师大版·数学】2024年中考一轮复习之垂线段最短
试卷更新日期:2023-11-05 类型:一轮复习
一、选择题
-
1. 如图是小明同学在体育课上跳远后留下的脚印,他的跳远成绩是线段( )的长度,这样测量的依据是( )
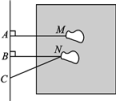 A、 , 两点之间,线段最短 B、 , 两点确定一条直线 C、 , 垂线段最短 D、 , 三角形两边之和大于第三边2. 如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A、 , 两点之间,线段最短 B、 , 两点确定一条直线 C、 , 垂线段最短 D、 , 三角形两边之和大于第三边2. 如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )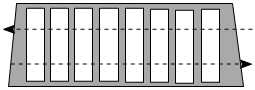 A、垂线段最短 B、两点确定一条直线 C、两点之间,线段最短 D、过直线外一点有且只有一条直线与已知直线平行3. 如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的数学道理是( )
A、垂线段最短 B、两点确定一条直线 C、两点之间,线段最短 D、过直线外一点有且只有一条直线与已知直线平行3. 如图,从人行横道线上的点P处过马路,沿线路PB行走距离最短,其依据的数学道理是( ) A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、在同一平面内,过一点有且只有一条直线与已知直线垂直4. 如图所示,△ACB中,∠ACB=90°,CD⊥AB于D,则下列结论:①BC>CD;②AC>AD;③AB>AC;④BC>AD.正确的有( )
A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、在同一平面内,过一点有且只有一条直线与已知直线垂直4. 如图所示,△ACB中,∠ACB=90°,CD⊥AB于D,则下列结论:①BC>CD;②AC>AD;③AB>AC;④BC>AD.正确的有( )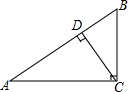 A、1个 B、2个 C、3个 D、4个5. 如图,在平面内过点O作已知直线m的垂线,可作垂线的条数有( )
A、1个 B、2个 C、3个 D、4个5. 如图,在平面内过点O作已知直线m的垂线,可作垂线的条数有( )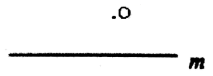 A、0条 B、1条 C、2条 D、无数条6. 如图,在中, , , , 点是上的动点,则的最小值为( )
A、0条 B、1条 C、2条 D、无数条6. 如图,在中, , , , 点是上的动点,则的最小值为( )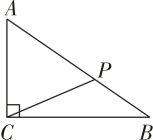 A、 B、 C、 D、7. 点A为直线外一点,于点C, . 点P是直线上的动点,则线段长可能是( )A、1 B、3 C、5 D、78. 如图,的半径为 , 弦 , 是弦上的一个动点,则的长度范围是( )
A、 B、 C、 D、7. 点A为直线外一点,于点C, . 点P是直线上的动点,则线段长可能是( )A、1 B、3 C、5 D、78. 如图,的半径为 , 弦 , 是弦上的一个动点,则的长度范围是( )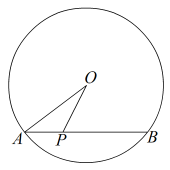 A、 B、 C、 D、9. 如图,在中, , , , 点P为边上任意一点,连接 , 以 , 为邻边作 , 连接 , 则长度的最小值为( )
A、 B、 C、 D、9. 如图,在中, , , , 点P为边上任意一点,连接 , 以 , 为邻边作 , 连接 , 则长度的最小值为( )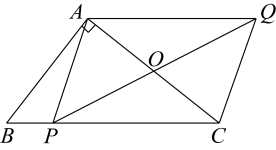 A、 B、 C、 D、10. 如图,在中,以点A为圆心,以适当长为半径作弧,分别交 , 于点E,F,再分别以E、F为圆心,以相同长度为半径作弧,两弧相交于点O,P为射线上任意一点,过点P作 , 交于点M,连接 , 若 , , 则长度的最小值为( )
A、 B、 C、 D、10. 如图,在中,以点A为圆心,以适当长为半径作弧,分别交 , 于点E,F,再分别以E、F为圆心,以相同长度为半径作弧,两弧相交于点O,P为射线上任意一点,过点P作 , 交于点M,连接 , 若 , , 则长度的最小值为( )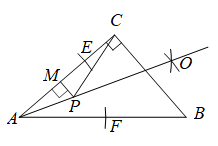 A、 B、 C、4 D、
A、 B、 C、4 D、二、填空题
-
11. 如图,在中, , , , 按下列步骤作图:①在和上分别截取、 , 使 . ②分别以点D和点E为圆心,以大于的长为半径作弧,两弧在内交于点M . ③作射线交于点F . 若点P是线段上的一个动点,连接 , 则的最小值是 .
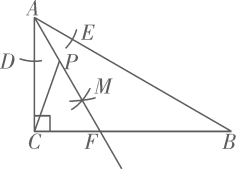 12. 如图,在直角坐标系中, , D是上一点,B是y正半轴上一点,且 , , 垂足为E ,
12. 如图,在直角坐标系中, , D是上一点,B是y正半轴上一点,且 , , 垂足为E ,
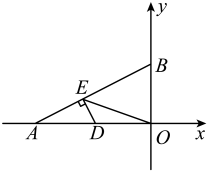 (1)、当D是的中点时,;(2)、求的最小值13. 如图,在中, , , 交于点D , P为线段上的动点,则的最小值为 .
(1)、当D是的中点时,;(2)、求的最小值13. 如图,在中, , , 交于点D , P为线段上的动点,则的最小值为 .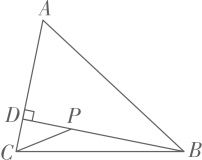 14. 如图,在菱形中, , , 点为对角线不含点上任意一点,则的最小值为 .
14. 如图,在菱形中, , , 点为对角线不含点上任意一点,则的最小值为 .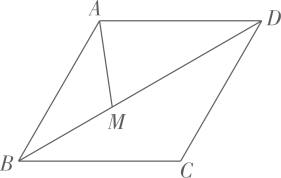 15. 在直角坐标系中,O为原点,P是直线y=-x+4上的动点,则|OP|的最小值为
15. 在直角坐标系中,O为原点,P是直线y=-x+4上的动点,则|OP|的最小值为三、作图题
-
16. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
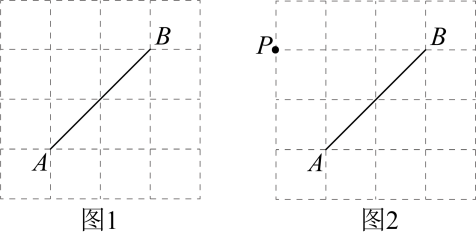 (1)、在图1中作锐角 , 使点C在格点上;(2)、在图2中的线段上作点Q,使最短.
(1)、在图1中作锐角 , 使点C在格点上;(2)、在图2中的线段上作点Q,使最短.四、解答题
-
17. 如图,在△ABC中,点P是BC边上的动点,点M是AP的中点,PD⊥AB , 垂足为D , PE⊥AC , 垂足为E , 连接MD , ME .
(Ⅰ)求证:∠DME=2∠BAC;
(Ⅱ)若∠B=45°,∠C=75°,AB= ,连接DE , 求△MDE周长的最小值.

五、综合题
-
18. 【综合与实践】我国海域的岛屿资源相当丰富,总面积达72800多平方公里,有人居住的岛屿达450个.位于北部湾的某小岛,外形酷似橄榄球,如图10-1所示.
如图10-2所示,现把海岸线近似看作直线m,小岛面对海岸线一侧的外缘近似看作
AB,经测量,AB的长可近似为250π海里,它所对的圆心角(∠AOB)的大小可近似为90°.(注:AB在m上的正投影为图中线段CD,点O在m上的正投影落在线段CD上.)
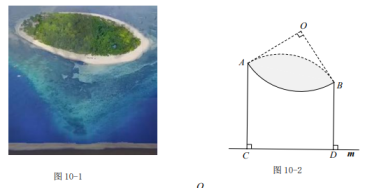
 (1)、求AB的半径r;(2)、因该岛四面环海,淡水资源缺乏,为解决岛上居民饮用淡水难的问题,拟在海岸线上,建造一个淡水补给站,向岛上居民输送淡水.为节约运输成本,要求补给站到小岛外缘AB的距离最近(即,要求补给站与AB上的任意一点,两点之间的距离取得最小值.);
(1)、求AB的半径r;(2)、因该岛四面环海,淡水资源缺乏,为解决岛上居民饮用淡水难的问题,拟在海岸线上,建造一个淡水补给站,向岛上居民输送淡水.为节约运输成本,要求补给站到小岛外缘AB的距离最近(即,要求补给站与AB上的任意一点,两点之间的距离取得最小值.);请你依据所学几何知识,在图10-2中画出补给站位置及最短运输路线.(保留画图痕迹,并做必要标记与注明;不限于尺规作图,不要求证明.)
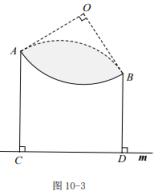
(3)、如图10-3,若测得AC长为600海里,BD长为500海里,试求出(2)中的最小距离。19. 如图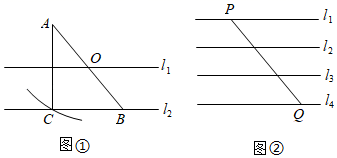 (1)、如图①,O为AB的中点,直线l1、l2分别经过点O、B,且l1∥l2 , 以点O为圆心,OA长为半径画弧交直线l2于点C,连接AC.求证:直线l1垂直平分AC;(2)、如图②,平面内直线l1∥l2∥l3∥l4 , 且相邻两直线间距离相等,点P、Q分别在直线l1、l4上,连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)20. 如图,一艘渔船位于小岛 的北偏东30°方向,距离小岛 的点 处,它沿着点 的南偏东15°方向航行.
(1)、如图①,O为AB的中点,直线l1、l2分别经过点O、B,且l1∥l2 , 以点O为圆心,OA长为半径画弧交直线l2于点C,连接AC.求证:直线l1垂直平分AC;(2)、如图②,平面内直线l1∥l2∥l3∥l4 , 且相邻两直线间距离相等,点P、Q分别在直线l1、l4上,连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)20. 如图,一艘渔船位于小岛 的北偏东30°方向,距离小岛 的点 处,它沿着点 的南偏东15°方向航行.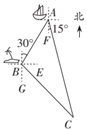 (1)、渔船航行多远与小岛 的距离最近?(结果保留根号)(2)、渔船到达距离小岛 最近点后,按原航向继续航行 到点 处时突然发生事故,渔船马上向小岛 上的救援队求救,问:救援队从 处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少?(结果保留根号)21. 如图,△ABC和△ADE中,AB=AD=6,BC=DE , ∠B=∠D=30°,边AD与边BC交于点P(不与点B , C重合),点B , E在AD异侧,I为△APC的内心.
(1)、渔船航行多远与小岛 的距离最近?(结果保留根号)(2)、渔船到达距离小岛 最近点后,按原航向继续航行 到点 处时突然发生事故,渔船马上向小岛 上的救援队求救,问:救援队从 处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少?(结果保留根号)21. 如图,△ABC和△ADE中,AB=AD=6,BC=DE , ∠B=∠D=30°,边AD与边BC交于点P(不与点B , C重合),点B , E在AD异侧,I为△APC的内心. (1)、求证:∠BAD=∠CAE;(2)、设AP=x , 请用含x的式子表示PD , 并求PD的最大值;(3)、当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m , n的值.
(1)、求证:∠BAD=∠CAE;(2)、设AP=x , 请用含x的式子表示PD , 并求PD的最大值;(3)、当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m , n的值.
-
-