备考2024年浙江中考数学一轮复习专题3.3整式 模拟集训
试卷更新日期:2023-11-05 类型:一轮复习
一、选择题(每题3分,共30分)
-
1. 与是同类项的为( )A、 B、 C、2 D、2. 计算的结果是( )A、 B、 C、 D、3. 下列计算中,正确的是( )A、 B、 C、 D、4. 下列式子计算结果等于的是( )A、 B、 C、 D、5. 已知 , , 则的值是( )A、 B、20 C、10 D、506. 如果 , 那么、的值分别是( ).A、 , B、 , C、 , D、 ,7. 如果能被整除,则的值是( )A、2 B、 C、3 D、8. 我国在清朝时期的课本中用“”来表示代数式 , 那么“”的化简结果是( )A、 B、 C、 D、9. 如图,将两张全等的矩形(非正方形)纸片先后放在同一个正方形中,按如图1呈轴对称方式放置,按如图2呈中心对称方式放置,若已知图形⑤的周长,则一定能求出( )
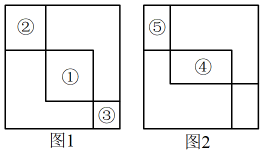 A、图形①与③的周长和 B、图形②与③的周长差 C、图形①与③的周长差 D、图形②与③的周长和10. 以直角三角形的各边为边分别向外作正方形(如图1),再把较小的两个正方形按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A、图形①与③的周长和 B、图形②与③的周长差 C、图形①与③的周长差 D、图形②与③的周长和10. 以直角三角形的各边为边分别向外作正方形(如图1),再把较小的两个正方形按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )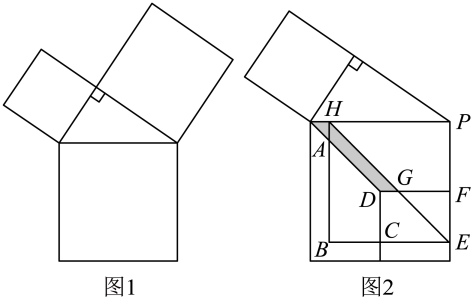 A、四边形的面积 B、四边形的面积 C、四边形的面积 D、的面积
A、四边形的面积 B、四边形的面积 C、四边形的面积 D、的面积二、填空题(每题4分,共24分)
-
11. 如果单项式 与 是同类项,那么 .12. 已知 , ,则 .13. 当 , 时,代数式的值是.14. 已知点在一次函数图象上,则的最小值为 .15. 已知 , 那么的值等于.16. 在某次演讲比赛中,五位评委给选手圆圆打分,得到互不相等的五个分数.若去掉一个最高分,平均分为x;去掉一个最低分,平均分为y;同时去掉一个最高分和一个最低分,平均分为z,则x, y,z的大小关系是(用“<”连接).
三、计算题
-
17.(1)、计算:;(2)、化简: .18. 计算:(1)、(2)、 ;(3)、 ;(4)、 .
四、解答题(共3题,共42分)
-
19. 已知多项式 与另一个多项式 的乘积为多项式 .(1)、若 为关于 的一次多项式 中 的一次项系数为0,直接写出 的值;(2)、若 为 ,求 的值.(3)、若 为关于 的二次多项式 ,判断 是否可能为关于 的三次二项式,如果可能,请求出b,c的值;如果不可能,请说明理由.

