备考2024年浙江中考数学一轮复习专题3.2整式真题集训

试卷更新日期：2023-11-05 类型：一轮复习

进入出卷网下载

一、选择题（每题3分，共30分）

1. （） $\times a b = 2 a b^{2}$ ，则括号内应填的单项式是（）

A、2 B、2a C、2b D、4b

查看试题解析
2. 计算2a²·3 a⁴的结果是（）

A、5a⁶ B、5a⁸ C、6a⁶ D、 6a⁸

查看试题解析
3. 下列计算正确的是（）

A、 $a^{6} \div a^{2} = a^{3}$ B、 ${(- a^{2})}^{5} = - a$ C、 $(a + 1) (a - 1) = a^{2} - 1$ D、 $(a + 1)^{2} = a^{2} + 1$

查看试题解析
4. 下列乘法公式的运用中，不正确的是（）

A、 $(2 x - 3) (2 x + 3) = 4 x^{2} - 9$ B、 ${(- 4 x - 1)}^{2} = 16 x^{2} - 8 x + 1$ C、 ${(3 - 2 a)}^{2} = 4 a^{2} + 9 - 12 a$ D、 $(- 2 x + 3 y) (3 y + 2 x) = 9 y^{2} - 4 x^{2}$

查看试题解析
5. 已知 $M = 2022^{2} ， N = 2021 \times 2023$ ，则 $M$ 与 $N$ 的大小关系是（）

A、 $M > N$ B、 $M < N$ C、 $M = N$ D、不能确定

查看试题解析
6. 已知（a+b）²＝49，a²+b²＝25，则ab＝（）

A、24 B、48 C、12 D、2 $\sqrt{6}$

查看试题解析
7. 已知a是任何实数，若M＝（2a﹣3）（3a﹣1），N＝2a（a﹣ $\frac{3}{2}$ ）﹣1，则M、N的大小关系是（）

A、M≥N B、M＞N C、M＜N D、M，N的大小由a的取值范围

查看试题解析
8. 下面是一位同学做的四道题：① ${(a + b)}^{2} = a^{2} + b^{2}$ .② ${(- 2 a^{2})}^{2} = - 4 a^{4}$ .③ $a^{5} \div a^{3} = a^{2}$ .④ $a^{3} \cdot a^{4} = a^{12}$ .其中做对的一道题的序号是（）

A、① B、② C、③ D、④

查看试题解析
9. 如图，在一个大长方形中放入三个边长不等的小正方形①、②、③，若要求出两个阴影部分周长的差，只要知道下列哪个图形的面积（）

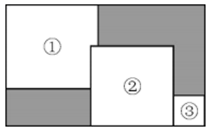A、正方形① B、正方形② C、正方形③ D、大长方形

查看试题解析
10. 在矩形ABCD内，将两张边长分别为a和b（a>b）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S₁ ，图2中阴影部分的面积为S₂ ．当AD-AB=2时，S₂-S₁的值为（）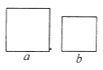

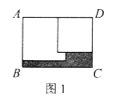
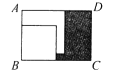A、2a B、2b C、2a-2b D、-2b

查看试题解析

二、填空题（每题4分，共24分）

11. 若 $x + y + z = 2 ， x^{2} - {(y + z)}^{2} = 8$ ，则 $x - y - z$ =.

查看试题解析
12. $（ \sqrt{6} + \sqrt{5} ）^{2021} \times （ \sqrt{6} - \sqrt{5} ）^{2022}$ = ．

查看试题解析
13. 已知 $4 m^{2} - 9 n^{2} = 26 ， 2 m + 3 n = 13$ ，则 $2 m - 3 n =$ .

查看试题解析
14. 一个正方形的面积为 $x^{2} + 4 x + 4 (x > 0)$ ，则它的边长为

查看试题解析
15. 已知关于x，y的方程组为 ${\begin{matrix} x + y = 3 + 2 a \\ x - y = 1 + a \end{matrix}$ ，则 $2^{x} \div {(2^{y})}^{3}$ 的值为.

查看试题解析
16. 若9^a·27^b÷81^c＝9，则2c﹣a﹣ $\frac{3}{2}$ b的值为．

查看试题解析

三、计算题（共4题，共33分）

17. 计算：

(1)、 $(1 + \sqrt[3]{8})^{0} + | - 2 | - \sqrt{9}$ ．

(2)、 $(a + 3) (a - 3) + a (1 - a)$ ．

查看试题解析
18. 用简便方法计算.

(1)、 ${6.4}^{2} - {3.6}^{2}$ ；

(2)、 $2104^{2} - 104^{2}$ ；

(3)、 ${2.4}^{2} \times 9 - {1.3}^{2} \times 36$ .

查看试题解析
19. 已知 $x = \frac{1}{3}$ ，求 $(2 x + 1) (2 x - 1) + x （ 3 - 4 x ）$ 的值.

查看试题解析
20.

(1)、解不等式： $2 x - 3 > x + 1$ ．

(2)、已知 $a^{2} + 3 a b = 5$ ，求 $(a + b) (a + 2 b) - 2 b^{2}$ 的值．

查看试题解析

四、解答题（共3题，共33分）

21. 比较x²+1与2x的大小。

(1)、尝试(用“<”，“=”或“>”填空)：
①当x=1时，x²+12x；

②当x=0时，x²+12x；

③当x=-2时，x²+12x。

(2)、归纳：若x取任意实数，x²+1与2x有怎样的大小关系？试说明理由.

查看试题解析
22. 有一张边长为a厘米的正方形桌面，因为实际需要，需将正方形边长增加b厘米，木工师傅设计了如图所示的三种方案：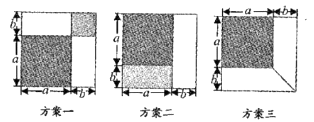

小明发现这三种方案都能验证公式：
a²+2ab+b²=（a+b）² ，
对于方案一，小明是这样验证的：
a²+ab+ab+b²=a²+2ab+b²=（a+b）²
请你根据方案二，方案三，写出公式的验证过程。

查看试题解析
23. 设 $a_{1} = 3^{2} - 1^{2} ， a_{2} = 5^{2} - 3^{2} ， \dots ， a_{n} = {(2 n + 1)}^{2} -$ ${(2 n - 1)}^{2} (n$ 为正整数).

(1)、探究 $a_{n}$ 是否为8的倍数，并用文字语言表述你所获得的结论；

(2)、若一个数的算术平方根是一个自然数，则称这个数是“完全平方数”.试找出 $a_{1} ， a_{2} ， \dots ， a_{n} ， \dots$ 这一列数中以小到大排列的前4个完全平方数，并指出当 $n$ 满足什么条件时， $a_{n}$ 为完全平方数(不必说明理间).

查看试题解析

备考2024年浙江中考数学一轮复习专题3.2整式 真题集训

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、计算题（共4题，共33分）

四、解答题（共3题，共33分）

备考2024年浙江中考数学一轮复习专题3.2整式真题集训