备考2024年浙江中考数学一轮复习专题3.1整式基础夯实

试卷更新日期：2023-11-05 类型：一轮复习

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列说法正确的有（）
(1) $\sqrt{3} a$ 不是整式；（2） $\frac{2 + b}{2}$ 是单项式；（3） $\frac{3}{4}$ 是整式；（4） $x + \frac{1}{x}$ 是多项式；（5） $\frac{a b}{π}$ 是单项式；（6） $x^{2} + 2 x + 1 = 0$ 是多项式

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列说法中，正确的是（）

A、 $- \frac{1}{2} x^{2} y$ 的系数是 $\frac{1}{2}$ B、 $x^{2} - 1$ 的常数项是1 C、 $4 x^{2} y$ 次数是2次 D、 $2 x^{2} - x + 2$ 是二次多项式

查看试题解析
3. 如果单项式2x³y⁴与-2x^ay^2b是同类项，那么a、b的值分别是（）

A、3，2 B、2，2 C、3，4 D、2，4

查看试题解析
4. $- [a - (b + c)]$ 去括号后应为（）

A、 $- a - b + c$ B、 $- a + b - c$ C、 $- a - b - c$ D、 $- a + b + c$

查看试题解析
5. 图1是由3个相同小长方形拼成的图形其周长为24 $c m$ ，图2中的长方形 $A B C D$ 内放置10个相同的小长方形，则长方形 $A B C D$ 的周长为（）

A、 $32 c m$ B、 $36 c m$ C、 $48 c m$ D、 $60 c m$

查看试题解析
6. 下列运算，结果正确的是（）

A、 $3 a + 2 a = 5 a^{2}$ B、 $3 a - 2 a = 1$ C、 $a^{2} \cdot a^{3} = a^{5}$ D、 $a \div a^{2} = a$

查看试题解析
7. 一个长方体，它的底面是边长为 $2 a^{3} b$ 的正方形，高为 $3 a b$ ，它的体积是（）

A、 $6 a^{6} b^{3}$ B、 $12 a^{6} b^{3}$ C、 $6 a^{7} b^{3}$ D、 $12 a^{7} b^{3}$

查看试题解析
8. 如果 $x^{3} + a x^{2} + b x + 8$ 能被 $x^{2} + 3 x + 2$ 整除，则 $\frac{b}{a}$ 的值是（）

A、2 B、 $\frac{1}{2}$ C、3 D、 $\frac{1}{3}$

查看试题解析
9. 设 $m = a + b$ ， $n = a b$ ， $p = a^{2} + b^{2}$ ， $q = a^{2} - b^{2}$ ，其中 $a = 2023 + t$ ， $b = 2021 + t$ ，给出以下结论：
$①$ 当 $n = 4$ 时， $p = 12$ ； $②$ 不论 $t$ 为何值， $\frac{p}{q} = \frac{n + 2}{m}$ ．

则下列判断正确的是（）

A、 $①$ ， $②$ 都对 B、 $①$ ， $②$ 都错 C、 $①$ 对， $②$ 错 D、 $①$ 错， $②$ 对

查看试题解析
10. 用若干个形状，大小完全相同的长方形纸片围成正方形， $4$ 个长方形纸片围成如图 $1$ 所示的正方形，其阴影部分的面积为 $100$ ； $8$ 个长方形纸片围成如图 $2$ 所示的正方形，其阴影部分的面积为 $81$ ； $12$ 个长方形纸片围成如图 $3$ 所示的正方形，其阴影部分的面积为（）

A、 $24$ B、 $32$ C、 $49$ D、 $64$

查看试题解析

二、填空题（每题2分，共12分）

11. 单项式 $\frac{3 a^{2} b}{2}$ 的系数是，次数是．

查看试题解析
12. 合并同类项 $2 x - 7 y - 5 x + 11 y - 1 =$ .

查看试题解析
13. 定义：若 $a + b = a b$ ，则称a、b是“西溪数”，例如： $3 + 1.5 = 3 \times 1.5$ ，因此3和1.5是一组“西溪数”，若m、n是一组“西溪数”，则 $2 m n - (3 m n - m - n - 6)$ 的值为．

查看试题解析
14. 观察下列等式：2+2²＝2³-2，2+2²+2³＝2⁴-2，2+2²+2³+2⁴＝2⁵-2…，若2⁵⁰＝m ，则2¹⁰¹+2¹⁰¹+2¹⁰²+…+2²⁰¹＝．（用含m的代数式表示）

查看试题解析
15. 计算： $(\sqrt{5} - 2)^{2022} (\sqrt{5} + 2)^{2023}$ 的结果是．

查看试题解析
16. 如图，一个长、宽、高分别为a，b， $2 r$ 的长方体纸盒装满了一层半径为r的小球，则纸盒的空间利用率（小球总体积与纸箱容积的比）为（结果保留 $π$ ，球体积公式 $V = \frac{4}{3} π r^{3}$ ）．

查看试题解析

三、计算题（共5题，共43分）

17. 计算：

(1)、 $| - 2 | + {(\frac{1}{2})}^{- 1} - {(π - 3.14)}^{0} - \sqrt[3]{27}$ ；

(2)、 ${(- \frac{1}{2} a^{2} b)}^{3} \cdot (- 8 a b^{3}) \div (- \frac{1}{2} a^{4} b^{2})$ ；

(3)、 $(- a + b - c) (a - b - c)$ ；

(4)、 $99.8 \times 100.2$ （用平方差公式计算）.

查看试题解析
18. 计算或化简：

(1)、 ${(- x^{2})}^{3} \cdot x^{4}$

(2)、 $(\frac{1}{3})^{2022} \times (- 3)^{2021}$

(3)、 ${(m + 1)}^{2} - (m + 1) (m - 1) + 2 m (m - 1)$

(4)、 $(a^{4} - 8 a^{2} + 16) \div (a^{2} + 4 a + 4)$

查看试题解析
19.

(1)、先化简，再求值： $m (m - 2 n) + {(m + n)}^{2} - (m + n) (m - n)$ ，其中 $m = - 1$ ， $n = 4$ ；

(2)、已知 $x + y = 3$ ， $x y = 2$ ，求 ${(x - y)}^{2}$ 的值．

查看试题解析
20. 已知 $x + y = 3$ ， $x y = 2$ .

(1)、求 $3^{x} \cdot 3^{y} - (3^{x})^{y}$ 的值.

(2)、求 $(7 - x) (7 - y)$ 的值.

(3)、求 $(x - y)^{2}$ 的值.

查看试题解析
21. 以下是方方化简 $(2 x + y) (2 x - y) + 4 (x + y)^{2}$ 的解答过程．
解： $(2 x + y) (2 x - y) + 4 (x + y)^{2}$
$= 4 x^{2} - y^{2} + 4 (x^{2} + y^{2})$
$= 4 x^{2} - y^{2} + 4 x^{2} + y^{2}$
$= 8 x^{2}$ ．
方方的解答过程是否有错误？如果有错误，写出正确的解答过程．

查看试题解析

四、解答题（共6题，共48分）

22. 已知多项式 $A = 3 x^{2} - x + 1$ ， $B = k x^{2} - (2 x^{2} + x - 2)$ ．

(1)、当 $x = - 1$ 时，求A的值；

(2)、小华认为无论 $k$ 取何值， $A - B$ 的值都无法确定．小明认为 $k$ 可以找到适当的数，使代数式 $A - B$ 的值是常数．你认为谁的说法正确？请说明理由．

查看试题解析
23. 观察下面的等式： $3^{2} - 1^{2} = 8 \times 1 ， 5^{2} - 3^{2} = 8 \times 2 ， 7^{2} - 5^{2} = 8 \times 3 ， 9^{2} - 7^{2} = 8 \times 4 ， ⋯$

(1)、写出 $1 9^{2} - 1 7^{2}$ 的结果．

(2)、按上面的规律归纳出一个一般的结论（用含n的等式表示，n为正整数）

(3)、请运用有关知识，推理说明这个结论是正确的．

查看试题解析
24. 观察下列式子，定义一种新运算：
$5 ⊙ 3 = 4 \times 5 + 3$ ； $3 ⊙ (- 1) = 4 \times 3 - 1$ ； $- 4 ⊙ (- 3) = 4 \times (- 4) - 3$ ；

(1)、这种新运算是： $a ⊙ b =$ $($ 用含 $a$ ， $b$ 的代数式表示 $)$ ；

(2)、如果 $a ⊙ (- 6) = 3 ⊙ a$ ，求 $a$ 的值；

(3)、若 $a$ ， $b$ 为整数，试判断 $(a ⊙ b - b ⊙ a) ⊙ 3 a$ 是否能被 $3$ 整除．

查看试题解析
25. 已知实数x ， y满足：x+y＝7，xy＝12．

(1)、求x²+y²的值；

(2)、将长方形ABCD和长方形CEFG按照如图方式放置，其中B ， C ， G三点在同一条直线上，连接BD ， BF ， AB＝nx ， FG＝y ，阴影部分的面积为14，求n的值．

查看试题解析
26. 如图，C为线段AB上一点， $A C = 4$ ， $B C = 2$ ，射线 $C D ⊥ A B$ 于点C，P为射线CD上一点，连接PA，PB.

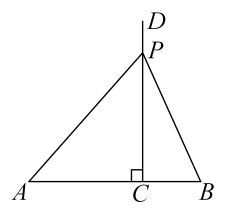(1)、【发现、提出问题】
①当 $P C = 3$ 时，求 $P A^{2} - P B^{2}$ 的值；

②小亮发现PC取不同值时， $P A^{2} - P B^{2}$ 的值存在一定规律，请猜想该规律.

(2)、【分析、解决问题】请证明你的猜想.

(3)、【运用】当 $P A - P B = 1$ 时， $△ P A B$ 的周长为.

查看试题解析
27. 如图 $1$ 是一个长为 $4 a$ ，宽为 $b$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成如图 $2$ 的正方形．

(1)、由图 $2$ 可以直接写出 $(a + b)^{2}$ ， $(a - b)^{2}$ ， $a b$ 之间的一个等量关系是；

(2)、根据(1)中的结论，解决下列问题： $3 x + 4 y = 10$ ， $x y = 2$ ，求 $3 x - 4 y$ 的值；

(3)、两个正方形 $A B C D$ ， $A E F G$ 如图 $3$ 摆放，边长分别为 $x$ ， $y .$ 若 $x^{2} + y^{2} = 58$ ， $B E = 4$ ，求图中阴影部分面积和．

查看试题解析

五、实践探究题（共2题，共17分）

28. 定义：任意两个数 $a$ ， $b$ ，按规则 $c = (a + 1) (b + 1)$ 运算得到一个新数 $c$ ，称所得的新数 $c$ 为 $a$ ， $b$ 的“和积数”．

(1)、若 $a = 4$ ， $b = - 2$ ，求 $a$ ， $b$ 的“和积数” $c$ ；

(2)、若 $a b = \frac{1}{2}$ ， $a^{2} + b^{2} = 8$ ，求 $a$ ， $b$ 的“和积数” $c$ ；

(3)、已知 $a = x + 1$ ，且 $a$ ， $b$ 的“和积数” $c = x^{3} + 4 x^{2} + 5 x + 2$ ，求 $b ($ 用含 $x$ 的式子表示 $)$ 并计算 $a + b$ 的最小值．

查看试题解析
29. 阅读材料：我们把多项式 $a^{2} + 2 a b + b^{2}$ 及 $a^{2} - 2 a b + b^{2}$ 叫做完全平方式．如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式的最大值，最小值等．
例如：分解因式： $x^{2} + 2 x - 3 = (x^{2} + 2 x + 1) - 4 = {(x + 1)}^{2} - 4 = (x + 1 + 2) (x + 1 - 2) = (x + 3) (x - 1)$ ；

又例如：求代数式 $2 x^{2} + 4 x - 6$ 的最小值：∵ $2 x^{2} + 4 x - 6 = 2 (x^{2} + 2 x - 3) = 2 {(x + 1)}^{2} - 8$ ，

又∵ ${(x + 1)}^{2} \geq 0$ ；

∴当 $x = - 1$ 时， $2 x^{2} + 4 x - 6$ 有最小值，最小值是 $- 8$ ．

根据阅读材料，利用“配方法”，解决下列问题：

(1)、分解因式： $a^{2} + 6 a + 8 =$ ．

(2)、已知实数 $a$ ， $b$ 满足 $a^{2} - 8 b = 12 a - b^{2} - 52$ ，求 $2 a + b$ 的值；

(3)、当 $x =$ 、 $y =$ 时，多项式 $- 2 x^{2} - 2 x y - y^{2} + 8 x - 7$ 的最大值．

查看试题解析

备考2024年浙江中考数学一轮复习专题3.1整式 基础夯实

一、选择题（每题3分，共30分）

二、填空题（每题2分，共12分）

三、计算题（共5题，共43分）

四、解答题（共6题，共48分）

五、实践探究题（共2题，共17分）

备考2024年浙江中考数学一轮复习专题3.1整式基础夯实