2023-2024学年北师大版数学七年级上册期中测试卷培优卷

试卷更新日期：2023-11-04 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列计算中，错误的是（）

A、 $- 5 - (- 6) = - 11$ B、 $- 5 - (- 6) = 1$
C、 $- 2.5 - | - 2.5 | = - 5$ D、 $3 \frac{1}{2} - | - 3 \frac{1}{2} | = 0$

查看试题解析
2. 如图是由 $6$ 个立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上的小立方块的个数，则这个几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 点 $A$ 在数轴上距离原点 $3$ 个单位长度，且位于原点左侧，若将点 $A$ 移动 $5$ 个单位长度到点 $B$ ，此时点 $B$ 表示的数是（）

A、 $8$ B、 $2$ C、 $- 8$ D、 $- 8$ 或 $2$

查看试题解析
4. 一个长方体，从左面、上面看得到的图形及相关数据如图，则从正面看该几何体所得到的图形的面积为
从左面看从上面看

A、6 B、8 C、12 D、9

查看试题解析
5. 对于有理数 $a ， b$ ，定义一种新运算“ $※$ ”，规定： $a ※ b = | a | - | b | - | a - b |$ ，则 $2 ※ (- 3)$ 等于（）

A、 $- 2$ B、 $- 6$ C、 $0$ D、 $2$

查看试题解析
6. 如果 $a + b > 0$ ，且 $a b < 0$ ，那么（）

A、 $a > 1 ， b > 0$ B、 $a < 0 ， b < 0$ C、 $a > 0 ， b < 0$ D、a、b异号且其中负数的绝对值较小

查看试题解析
7. 在数轴上，表示数 $x$ 的点的位置如图所示，则化简 $| x + 2 | - | x - 1 |$ 的结果为（）

A、 $2 x + 1$ B、 $x + 3$ C、 $1$ D、 $3$

查看试题解析
8. 如图所示的程序计算，若开始输入的值为 $- \frac{1}{2}$ ，则输出的结果 $y$ 是（）

A、25 B、30 C、45 D、40

查看试题解析
9. 观察下列算式： $2^{1} = 2$ ； $2^{2} = 4$ ； $2^{3} = 8$ ； $2^{4} = 16$ ； $2^{5} = 32$ ；……，则 $2^{2003} + 3$ 的末尾数字是（）

A、1 B、5 C、7 D、9

查看试题解析
10. 下列从左到右的变式正确的是（）

A、-a+b+c=-（a+b-c） B、-（a-b+c）=-a+b-c C、a-b+c=-（a+b-c） D、-（a-b+c）=-a-b-c

查看试题解析

二、填空题（每题3分，共18分）

11. 如图，若要使图中平面展开图折叠成正方体后，相对面上两个数之和为 $6$ ，则 $x =$ ， $y =$ ．

查看试题解析
12. $| x - 2 | + | 2 x + y - 7 | = 0$ ，则 $(x - y)^{2021} =$ ．

查看试题解析
13. 计算 $2^{4} + \frac{1}{3} \times [{(- 3)}^{2} - 6]$ ＝．

查看试题解析
14. 小颖同学做这样―道题“计算 $| - 5 + Δ |$ ”，其中“△”是被墨水污染看不清的一个数，她翻开后面的答案，得知该题的计算结果是3，那么“△”表示的数是.

查看试题解析
15. 找出下列各图形中数的规律，依此可得a的值为．

查看试题解析
16. 定义： $a$ 是不为 $1$ 的有理数，我们把 $\frac{1}{1 - a}$ 称为 $a$ 的差倒数 $.$ 如： $2$ 的差倒数是 $\frac{1}{1 - 2} = - 1$ ， $- 1$ 的差倒数是 $\frac{1}{1 - (- 1)} = \frac{1}{2} .$ 已知 $a_{1} = \frac{1}{3} . a_{2}$ 是 $a_{1}$ 的差倒数， $a_{3}$ 是 $a_{2}$ 的差倒数， $a_{4}$ 是 $a_{3}$ 的差倒数， $\dots$ ，以此类推，则 $a_{2023} =$ ．

查看试题解析

三、解答题（共8题，共72分）

17. 计算：

(1)、 ${(- 3)}^{2} \times [- \frac{2}{3} + (- \frac{5}{9})]$ ；

(2)、 $- 1^{4} + (- 3) \times [{(- 4)}^{2} + 2] - {(- 2)}^{3} \div 4$ ；

查看试题解析
18. 计算：

(1)、-1-（1+0.5）× $\frac{1}{3}$ +（-4）；

(2)、-8²+3×（-2）²+（-6）+（- $\frac{1}{3}$ ）² ．

查看试题解析
19. 先化简，再求值：
$3 x^{2} y - [4 x y - 2 (2 x y - \frac{3}{2} x^{2} y) + x^{2} y^{2}]$ ，其中 $x = - 3 ， y = \frac{1}{3}$ ．

查看试题解析
20. 已知A=2a²-b+2，B=-a²-b+1．

(1)、求3A- 2B．

(2)、若a，b满足 $\sqrt{a + 1}$ +|b-2|=0，求3A-2B的值．

查看试题解析
21. 某模具厂规定每个工人每天生产模具 $40$ 个，由于各种原因，实际每天的生产量与规定量相比有出入 $.$ 下表是工人小张某一周的生产情况 $($ 超出记为正，不足记为负 $)$ ：
星期
一
二
三
四
五
六
日
增减产量
          $+ 9$
          $- 13$
          $- 4$
          $+ 8$
          $- 14$
          $+ 7$
          $+ 3$

(1)、根据记录的数据计算小张本周实际生产模具的数量；

(2)、该厂实行“每日计件工资制”，每生产一个玩具可得工资 $5$ 元，若超额完成任务，则超过部分每个另奖 $4$ 元，少生产一个则倒扣 $2$ 元，计算小张这一周的工资总额是多少元？

查看试题解析
22. 从上面看到的形状图中的小正方形中的字母表示在该位置上小立方块的个数，请解答下列问题：

(1)、a= ， b= ， c=；

(2)、这个几何体最少由个小立方块搭成，最多由个小立方块搭成；

(3)、当d=e=1，f=2时，在网格图中画出这个几何体从左面看到的形状图.

查看试题解析
23. 【阅读材料】问题：如何计算 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \cdot \cdot \cdot + \frac{1}{19 \times 20}$ 呢？小红带领的数学兴趣小组通过探索完成了这道题的计算．
他们的解法如下：
解：原式＝ $= (1 - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) + ⋯ + (\frac{1}{19} - \frac{1}{20}) = 1 - \frac{1}{20} = \frac{19}{20}$ ．
根据材料，请你完成下列计算：

(1)、计算： $\frac{2}{1 \times 3} + \frac{2}{3 \times 5} + \frac{2}{5 \times 7} + \frac{2}{7 \times 9} + \frac{2}{9 \times 11}$ ；

(2)、直接写出结果： $\frac{1}{3} + \frac{1}{15} + \frac{1}{35} + \frac{1}{63} + \frac{1}{99}$ ＝；

(3)、计算： $\frac{1}{1 \times 5} + \frac{1}{5 \times 9} + \frac{1}{9 \times 13} + ⋯ + \frac{1}{2015 \times 2019} + \frac{1}{2019 \times 2023}$ ．

查看试题解析
24. 如图①，现有三种边长分别为3，2，1的正方形卡片，分别记为Ⅰ，Ⅱ，Ⅲ.还有一个长为a，宽为b的长方形.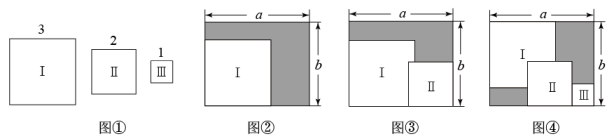

(1)、如图②，将Ⅰ放入长方形中，试用含a，b的代数式表示阴影部分的面积，并求当 $a = 4.5$ ， $b = 4$ 时阴影部分的面积.

(2)、将Ⅰ，Ⅱ两张卡片按图③的方式，放置在长方形中，试用含a，b的代数式表示阴影部分的面积，并求当 $a = 4.5$ ， $b = 4$ 时阴影部分的面积.

(3)、将Ⅰ，Ⅱ，Ⅲ三张卡片按图④的方式，放置在长方形中，求右上角阴影部分与左下角阴影部分周长的差.

查看试题解析

星期	一	二	三	四	五	六	日
增减产量	$+ 9$	$- 13$	$- 4$	$+ 8$	$- 14$	$+ 7$	$+ 3$