人教版2023-2024学年九年级上学期期中数学模拟试题二（吉林地区专用）

试卷更新日期：2023-11-03 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列各式中是一元二次方程的是（）

A、 $x^{2} + x = 2 y$ B、 $x^{2} = 1$ C、 $a x^{2} + b x + c = 0$ D、 $x^{2} + x + 1$

查看试题解析
2. 若a，b，c是△ABC的三边长，则关于x的方程 $x^{2} - (a + b) x + \frac{1}{4} c^{2} = 0$ 的根的情况是（　　）

A、无实数根 B、有两相等的实数根 C、有两不相等的实数根 D、无法确定

查看试题解析
3. 已知 $x = 0$ 是关于x的一元二次方程 $(m + 1) x^{2} + m x + 4 m^{2} - 4 = 0$ 的一个解，则m的值是（　　）

A、1 B、 $- 1$ C、0或1 D、1或 $- 1$

查看试题解析
4. 抛物线 $y = x^{2} + 6 x + 5$ 可由抛物线 $y = x^{2}$ 平移得到，平移方法是（）

A、先向右平移3个单位，再向下平移4个单位 B、先向左平移6个单位，再向上平移5个单位 C、先向左平移3个单位，再向下平移4个单位 D、先回右平移3个单位，再向上平移1个单位

查看试题解析
5. 在平面直角坐标系中，抛物线 $y = x^{2} - 1$ 与坐标轴交点的个数是（）．

A、3 B、2 C、1 D、0

查看试题解析
6. 已知 $0 \leq x \leq \frac{1}{2}$ ，那么函数 $y = - 2 x^{2} + 8 x - 6$ 的最大值是（　　）

A、 $- \frac{5}{2}$ B、2 C、 $- 3$ D、 $- 6$

查看试题解析
7. 如图，将△ABC绕点C顺时针旋转90°得到△EDC．若∠ACB=20°，则∠ACD的度数是（）

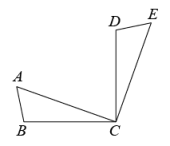A、55° B、60° C、65° D、70°

查看试题解析
8. 下列是有关北京2022年冬奥会的图片，其中是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 若 $(m - 3) x^{| m - 1 |} + (m + 1) x + 4 = 0$ 是关于x的一元二次方程，则m= ．

查看试题解析
10. 若一元二次方程 $x^{2} + 5 x - 6 = 0$ 的两个根是 $x_{1} ， x_{2}$ ，则 $x_{1} x_{2}$ 的值是．

查看试题解析
11. 抛物线y＝x²-2x与x轴的交点坐标是．

查看试题解析
12. 将二次函数 $y = - 3 x^{2} + 6 x$ 的图象绕顶点旋转180°所得抛物线解析式为.

查看试题解析
13. 在平面直角坐标系中，点 $(a + 2 ， 2)$ 关于原点的对称点为 $(4 ， - b)$ ，则 $a b$ 的值为.

查看试题解析
14. 如图，已知正方形ABCD的边长为6，E、F分别是AB、BC边上的点，且∠EDF＝45°，将△DAE绕点D逆时针旋转90°，得到△DCM若AE＝2，则FM的长为 .

查看试题解析

三、解答题

15. 解方程：

(1)、3x（x﹣4）=2（x﹣4）．

(2)、3x²﹣5x﹣1＝0．

查看试题解析
16. 已知二次函数 $y = x^{2} + b x + c$ ，当 $x = 1$ 时， $y = 8$ ；当 $x = - 1$ 时， $y = 0$ .求这个二次函数的表达式.

查看试题解析
17. 如图所示，将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上.若AC $= \sqrt{3}$ ，∠B＝60°，求CD的长.

查看试题解析
18. 已知关于 $x$ 的一元二次方程 $x^{2} + 2 x - (n - 1) = 0$ 有两个实数根，求 $n$ 的取值范围．

查看试题解析
19. 如果关于 $x$ 的方程 $m x^{2} - 2 (m + 2) x + m + 5 = 0$ 没有实数根，试判断关于 $x$ 的方程 $(m - 5) x^{2} - 2 (m - 1) x + m = 0$ 的根的情况.

查看试题解析
20. 来自武汉高校的若干个社团参加了“敢为人先，追求卓越”的城市精神的研讨会，参加研讨会的每两个社团之间都签订了一份合作协议，所有社团共签订了45份协议，共有多少个社团参加研讨会？

查看试题解析

21. 根据以下素材，探索完成任务．

如何设计喷水池喷头的安装方案？
素材1	图1中有一个直径为20 m的圆形喷水池，四周安装一圈喷头，喷射水柱呈抛物线型，在水池中心O处立着一个直径为1 m的圆柱形实心石柱，各方向喷出的水柱在石柱顶部的中心点M处汇合，如图2，水柱距水池中心4 m处到达最高，高度为6 m．

素材2	如图3，拟在水池里过水池中心的直线上安装一排直线型喷头（喷射水柱竖直向上，高度均为 $\frac{21}{8}$ m）；相邻两个直线型喷头的间距均为1.2 m，且喷射的水柱不能碰到抛物线型水柱，要求在符合条件处都安装喷头，安装后关于OM成轴对称分布．
问题解决
任务1	确定水柱形状	在图2中建立合适的直角坐标系，任选一条抛物线求函数表达式．
任务2	确定石柱高度	在你所建立的坐标系中，确定水柱汇合点M的纵坐标．
任务3	拟定设计方案	请给出符合所有要求的直线型喷头的安装数量，并根据你所建立的直角坐标系，求出离中心O最远的两个直线型喷头的坐标．

查看试题解析

22. 如图，直线 $y = - \frac{1}{2} x + 2$ 与 $x$ 轴、 $y$ 轴分别交于 $B$ 、 $A$ 两点， $Q$ 是线段 $A B$ 上的动点（不与 $A$ 、 $B$ 重合），将 $Q$ 绕点 $P (1 ， 0)$ 顺时针旋转 $90 °$ 得到点 $Q'$ ，连接 $O Q'$ ，求 $O Q'$ 的最小值．

查看试题解析
23. 如图，将矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG，点B与点E对应，点E恰好落在AD边上，BH⊥CE交于点H，求证：AB＝BH．

查看试题解析
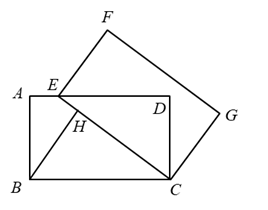24. 如图，在正方形ABCD中，点E，F分别是BC，CD边上的动点，且∠EAF＝45°，求证：EF＝DF+BE．观察：EF，DF，BE三条线段都不在同一条直线上，能不能借助图形的运动，将部分线段放置在一条直线上加以证明呢？思路：将△ABE绕点A顺时针旋转9O°使AB与AD重合，得到了旋转后的△ADG．
①根据上述思路在图中画图分析并证明（写出详细的证明过程）．
②若正方形ABCD的边长为6，当动点E在BC边上运动到中点位置时，动点F在CD边上距离D点多长的位置？

查看试题解析