人教版2023-2024学年八年级上学期期中数学模拟试题二(吉林地区专用)
试卷更新日期:2023-11-03 类型:复习试卷
一、选择题
-
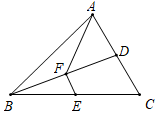
1. 如图,已知D、E分别为△ABC的边AC、BC的中点,AF为△ABD的中线,连接EF,若四边形AFEC的面积为15,且AB=8,则△ABC中AB边上高的长为( )
 A、3 B、6 C、9 D、无法确定2. 如图,直线 , 直线 , 若 , 则( )
A、3 B、6 C、9 D、无法确定2. 如图,直线 , 直线 , 若 , 则( ) A、 B、 C、 D、3. 如图,在中, , 点是延长线上一点,过点作 . 若 , 则的度数为( )
A、 B、 C、 D、3. 如图,在中, , 点是延长线上一点,过点作 . 若 , 则的度数为( ) A、20° B、30° C、40° D、50°4. 如图, , , 平分 , 则为( )
A、20° B、30° C、40° D、50°4. 如图, , , 平分 , 则为( ) A、 B、 C、 D、5. 如图, 于点 , 于点 , . 要根据证明 , 则还需要添加的条件是( )
A、 B、 C、 D、5. 如图, 于点 , 于点 , . 要根据证明 , 则还需要添加的条件是( ) A、 B、 C、 D、6. 如图,A , B , C , D在同一条直线上, , , 在下列条件中,不能使与全等的是( )
A、 B、 C、 D、6. 如图,A , B , C , D在同一条直线上, , , 在下列条件中,不能使与全等的是( ) A、 B、 C、 D、7. 等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )A、70° B、20° C、70°或20° D、40°或140°8. 如图,为线段的垂直平分线上一点,若 , 则的长为( )
A、 B、 C、 D、7. 等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )A、70° B、20° C、70°或20° D、40°或140°8. 如图,为线段的垂直平分线上一点,若 , 则的长为( )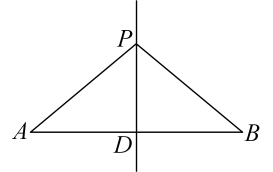 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,将一个直角三角板和一把直尺按如图所示的方式摆放,若 , 则的度数为 .
 10. 若多边形的每一个外角都等于60°,则该多边形的边数是.11. 如图所示,点在一块直角三角板上(其中),于点 , 于点 , 若 , 则度.
10. 若多边形的每一个外角都等于60°,则该多边形的边数是.11. 如图所示,点在一块直角三角板上(其中),于点 , 于点 , 若 , 则度.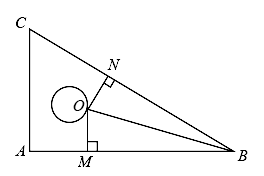 12. 如图,点P是平分线上一点, , 垂足为D,且 , 点M是射线上一动点,则的最小值为 .
12. 如图,点P是平分线上一点, , 垂足为D,且 , 点M是射线上一动点,则的最小值为 . 13. 如图,在中,于D , 若 , 则 .
13. 如图,在中,于D , 若 , 则 .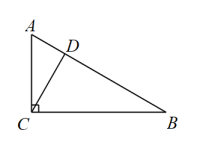 14. 如图,点C在线段 上, ,点E在 上,若 , ,则 的度数为 .
14. 如图,点C在线段 上, ,点E在 上,若 , ,则 的度数为 .
三、解答题
-
15. 如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=100°,求∠A和∠ACE的度数.
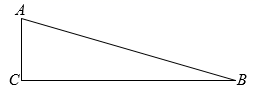
 16. 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD.若AE=6,△CBD的周长为20,求BC的长.
16. 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD.若AE=6,△CBD的周长为20,求BC的长. 17. 我们学习了平面图形的镶嵌,即用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,就是平面图形的镶嵌.镶嵌平面的图形有很多,值得我们研究的问题也有许多!如图,小亮同学用绘画的方法,设计的一个正三角形的平面镶嵌图,如果整个镶嵌图三角形ABC的面积为75,则图中阴影部分的面积是多少?
17. 我们学习了平面图形的镶嵌,即用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,就是平面图形的镶嵌.镶嵌平面的图形有很多,值得我们研究的问题也有许多!如图,小亮同学用绘画的方法,设计的一个正三角形的平面镶嵌图,如果整个镶嵌图三角形ABC的面积为75,则图中阴影部分的面积是多少?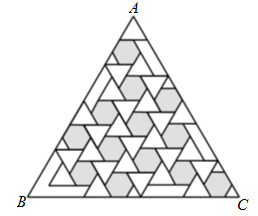 18. 探究归纳题:
18. 探究归纳题: (1)、试验分析:
(1)、试验分析:如图1,经过A点可以作条对角线;同样,经过B点可以作条;经过C点可以作条;经过D点可以作条对角线.
通过以上分析和总结,图1共有条对角线.
(2)、拓展延伸:运用(1)的分析方法,可得:
图2共有条对角线;
图3共有条对角线;
(3)、探索归纳:对于n边形(n>3),共有条对角线.(用含n的式子表示)
(4)、特例验证:十边形有条对角线.
19. 已知:如图, , 过AC上一点D,作交BC于点F.求证: .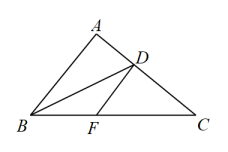 20. 如图,四边形中,平分 , 于点 , . 求证: .
20. 如图,四边形中,平分 , 于点 , . 求证: . 21. 如图,已知 , 平分交的延长线于点E,平分交的延长线于点F,且与交于点G,求证: .
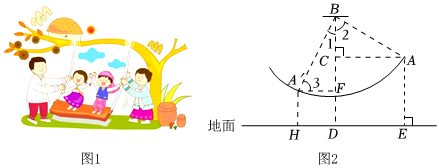
21. 如图,已知 , 平分交的延长线于点E,平分交的延长线于点F,且与交于点G,求证: . 22. 如图 , 是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线上,转轴到地面的距离乐乐在荡秋千过程中,当秋千摆动到最高点时,过点作于 , 点到地面的距离 , 当他从处摆动到处时, , 若 , 作 , 垂足为F.求到的距离 .
22. 如图 , 是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线上,转轴到地面的距离乐乐在荡秋千过程中,当秋千摆动到最高点时,过点作于 , 点到地面的距离 , 当他从处摆动到处时, , 若 , 作 , 垂足为F.求到的距离 .