人教版2023-2024学年八年级上学期期中数学模拟试题一(吉林地区专用)
试卷更新日期:2023-11-03 类型:复习试卷
一、选择题
-
1. 下列长度的三条线段能组成三角形的是( )A、3cm , 5cm , 7cm B、3cm , 3cm , 7cm C、4cm , 4cm , 8cm D、4cm , 5cm , 9cm2. 已知三角形的两边长分别为5和9,则该三角形的第三边长可能是( )A、3 B、4 C、5 D、143. 如图,点O是△ABC内一点,∠ABO=30°,∠ACO=15°,∠BOC=100°,则∠A的度数为( )
 A、40° B、45° C、55° D、不能确定4. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )
A、40° B、45° C、55° D、不能确定4. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=∠AOB的依据是( )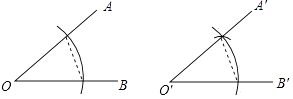 A、SAS B、ASA C、AAS D、SSS5. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A、SAS B、ASA C、AAS D、SSS5. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )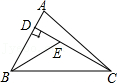 A、10 B、7 C、5 D、46. 如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A、10 B、7 C、5 D、46. 如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( ) A、4 B、3 C、2 D、1.57. 如图所示.在△ABC中,∠C=90°,DE垂直平分AB,交BC于点E,垂足为点D,BE=6cm,∠B=15°,则AC等于( )
A、4 B、3 C、2 D、1.57. 如图所示.在△ABC中,∠C=90°,DE垂直平分AB,交BC于点E,垂足为点D,BE=6cm,∠B=15°,则AC等于( ) A、6cm B、5cm C、4cm D、3cm8. 下列图案中,是轴对称图形的是( )A、
A、6cm B、5cm C、4cm D、3cm8. 下列图案中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 如图,在中, , , 为的平分线,则=.
 10. 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF;则以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC+∠ABD=90°;其中正确的结论有 .
10. 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF;则以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC+∠ABD=90°;其中正确的结论有 . 11. 如图,平分 , 于点 , 点为射线上一动点,若 , 则的最小值为 .
11. 如图,平分 , 于点 , 点为射线上一动点,若 , 则的最小值为 . 12. 在平面直角坐标系中,点A的坐标为 , 点B的坐标为 , 点C的坐标为 , 如果要使与全等,那么点D的坐标是 .13. 如图,在中, , , 于D,则的长为 .
12. 在平面直角坐标系中,点A的坐标为 , 点B的坐标为 , 点C的坐标为 , 如果要使与全等,那么点D的坐标是 .13. 如图,在中, , , 于D,则的长为 . 14. 小丽从一张等腰三角形纸片ABC(AB=AC)中恰好剪出五个如图所示的小等腰三角形,其中BC=BD,EC=EF=FG=DG=DA,则∠B=°.
14. 小丽从一张等腰三角形纸片ABC(AB=AC)中恰好剪出五个如图所示的小等腰三角形,其中BC=BD,EC=EF=FG=DG=DA,则∠B=°.
三、解答题
-
15. 如图,在中,是的角平分线,是边上的高,相交于点O,如果 , 求的度数.
 16. 如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=25°,求∠DAE的度数.
16. 如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=25°,求∠DAE的度数. 17. 如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示, , , , , 求 .
17. 如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示, , , , , 求 .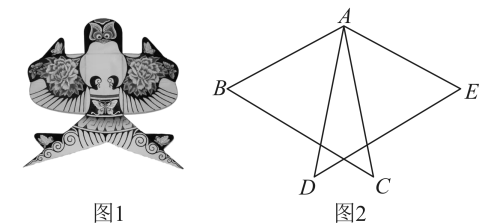 18. 如图, , , , .求的度数.
18. 如图, , , , .求的度数. 19. 已知:如图,在中, , 点D、E分别在边AC、AB上,且 , BD与CE相交于点O.求证:.
19. 已知:如图,在中, , 点D、E分别在边AC、AB上,且 , BD与CE相交于点O.求证:. 20. 如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF.
20. 如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF. 21. 已知三角形三边长分别为a , b , c , 其中a , b满足(a﹣8)2+|b﹣6|=0,求这个三角形的第三边长c的取值范围.22. 如图,工人师傅要检查三角形工件ABC的和是否相等,但他手边没有量角器,只有一个刻度尺,他是这样操作的:
21. 已知三角形三边长分别为a , b , c , 其中a , b满足(a﹣8)2+|b﹣6|=0,求这个三角形的第三边长c的取值范围.22. 如图,工人师傅要检查三角形工件ABC的和是否相等,但他手边没有量角器,只有一个刻度尺,他是这样操作的:
①分别在BA和CA上取
②在BC上取
③连接DE、FG,量出DE的长为a米,FG的长为b米.
若 , 则说明和是相等的,他的这种做法合理吗?为什么?
23. 某产品的商标如图所示,O是线段AC、DB的交点,且AC=BD,AB=DC,小林认为图中的两个三角形全等,他的思考过程是:∵ AC=DB,∠AOB=∠DOC,AB=DC,
∴ △ABO≌△DCO.
你认为小林的思考过程对吗?
如果正确,指出他用的是哪个判别三角形全等的方法;如果错误,写出你的思考过程
 24. 根据以下素材,探索完成任务.
24. 根据以下素材,探索完成任务.三角形背景下角的关系探索
素材1
如图,已知等腰△ABC中,BA=BC,在腰BC的延长线上取点E,连结AE,作AE的中垂线交射线BC于点D,连结AD.

素材2
研究一个几何问题时,一般先根据几何语言画出几何图形.可能需要分类讨论.
素材3
当我们要论证一个一般性结论时,常常将问题先分成几种特例,在研究特例的过程中寻求规律,总结方法,猜测结论,再将规律、方法和结论迁移到一般情形中,这种数学推理方法叫做归纳法.
问题解决
任务1
补全图形
请根据素材1,把图形补全.你画的点D在点C的 ▲ 侧.
任务2
特例猜想
有下列条件:①AB=AC;②∠B=40°;③∠CEA=20°;④∠CEA=50°;请从中选择你认为合适的一个或两个条件作为已知条件,求出∠BAD和∠CAE的大小,并猜测∠BAD与∠CAE的数量关系.
任务3
一般结论
请根据你在任务1中所画的一般情况下的图形,写出∠BAD与∠CAE的数量关系,并说明理由.
任务4
拓展延伸
除了你在任务1中所画的情形外,点D相对于点C的位置还有不同的情形吗?若有,请画出图形,并直接写出∠BAD与∠CAE的数量关系.