广西南宁市青秀区重点学校2022-2023学年八年级下学期数学期末试卷
试卷更新日期:2023-11-03 类型:期末考试
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列属于最简二次根式的是( )A、 B、 C、 D、2. 下列各曲线中,能表示是的函数的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一元二次方程的一次项系数是( )A、 B、 C、 D、4. 在中,若的度数是( )A、 B、 C、 D、5. 已知函数的图象是一条直线,下列说法正确的是( )A、直线过原点 B、随的增大而减小 C、直线经过点 D、直线经过第二、四象限6. 下表记录了甲、乙、丙、丁四位选手各次射击成绩的数据信息,请你根据表中数据选一人参加比赛,最合适的人选是( )
3. 一元二次方程的一次项系数是( )A、 B、 C、 D、4. 在中,若的度数是( )A、 B、 C、 D、5. 已知函数的图象是一条直线,下列说法正确的是( )A、直线过原点 B、随的增大而减小 C、直线经过点 D、直线经过第二、四象限6. 下表记录了甲、乙、丙、丁四位选手各次射击成绩的数据信息,请你根据表中数据选一人参加比赛,最合适的人选是( )选手
甲
乙
丙
丁
平均数环
方差环
A、甲 B、乙 C、丙 D、丁7. 一元二次方程的解为( )A、 , B、 , C、 D、8. 如图,直线:与直线:交于点 , 则不等式的解集是( ) A、 B、 C、 D、9. 定义一种新运算“”, , 则的值为( )A、 B、 C、 D、10. 年月是第个世界读书日,读书已经成为很多人的一种生活方式,城市书院是读书的重要场所之一,据统计,某书院对外开放的第一个月进书院人次,进书院人次逐月增加,到第三个月末累计进书院人次,若进书院人次的月平均增长率为 , 则可列方程为( )A、 B、 C、 D、11. 在同一坐标系中,一次函数与二次函数的图象可能是( )A、
A、 B、 C、 D、9. 定义一种新运算“”, , 则的值为( )A、 B、 C、 D、10. 年月是第个世界读书日,读书已经成为很多人的一种生活方式,城市书院是读书的重要场所之一,据统计,某书院对外开放的第一个月进书院人次,进书院人次逐月增加,到第三个月末累计进书院人次,若进书院人次的月平均增长率为 , 则可列方程为( )A、 B、 C、 D、11. 在同一坐标系中,一次函数与二次函数的图象可能是( )A、 B、
B、 C、
C、 D、
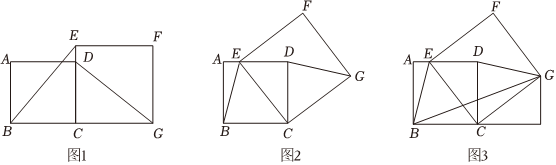
D、 12. 如图,在平面直角坐标系中,点 , , , 都在轴上,点 , , , 都在直线上, , , , 都是等腰直角三角形,且 , 则点的坐标是( )
12. 如图,在平面直角坐标系中,点 , , , 都在轴上,点 , , , 都在直线上, , , , 都是等腰直角三角形,且 , 则点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共12.0分)
-
13. 若二次根式 有意义,则x的取值范围是 .14. 如图,在中, , , , 则 .
 15. 将直线向上平移个单位长度,平移后直线的解析式为 .16. 为了增强青少年的防毒意识,学校举办了一次“禁毒教育”演讲比赛某位选手的演讲内容,语言表达,演讲技巧这三项成绩分别为分,分,分,若依次按 , , 的比例确定最终成绩,则该选手的比赛成绩是分17. 某学校航模组设计制作的火箭升空高度与飞行时间满足函数关系式为 , 当火箭升空到最高点时,距离地面18. 如图,正方形的边长为 , 点 , 分别在 , 上若 , , 则的长为 .
15. 将直线向上平移个单位长度,平移后直线的解析式为 .16. 为了增强青少年的防毒意识,学校举办了一次“禁毒教育”演讲比赛某位选手的演讲内容,语言表达,演讲技巧这三项成绩分别为分,分,分,若依次按 , , 的比例确定最终成绩,则该选手的比赛成绩是分17. 某学校航模组设计制作的火箭升空高度与飞行时间满足函数关系式为 , 当火箭升空到最高点时,距离地面18. 如图,正方形的边长为 , 点 , 分别在 , 上若 , , 则的长为 .
三、计算题(本大题共1小题,共6.0分)
-
19. 解方程:
四、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
20. 计算: .21. 在平面直角坐标系中如图所示.
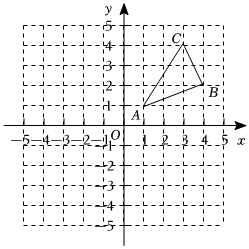
⑴请画出关于原点对称的 , 并写出 , 的坐标;
⑵将向右平移个单位得到 , 请画出;
⑶与关于点成中心对称,请直接写出点的坐标.
22. 广大青少年的身体和心理健康已经成为社会关注的话题,而学生的身体和心理健康教育需要学校和家庭共同承担某校在八、九年级家长中进行了“青少年身心健康知识”调查活动,并将调查结果用计算机折合成分数百分制 , 从八、九年级的家长调查卷中各随机抽取了名家长的折合分数,分数用表示,共分成四组,数据整理如下:A. , , ,
八年级名家长的分数是: , , , , , , , , , . 九年级名家长的分数在组中的数据是: , , .
抽取的八、九年级家长分数统计表:
年级
平均数
中位数
众数
方差
八年级
九年级
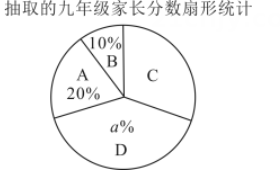
根据以上信息,解答下列问题:(1)、直接写出上述 , , 的值: , , ;(2)、该校八、九年级分别有名、名家长参加了此次调查活动,请估计两个年级分数低于分的家长总人数;(3)、根据以上数据,你认为该校八、九年级哪个年级家长对“青少年身心健康知识”了解得更好?请说明理由写出一条理由即可 .23. 如图,在矩形中,点是对角线的中点,过点作交于点 , 交于点 , 连接 , . (1)、求证:四边形是菱形;(2)、若 , , 求四边形的面积.24. 甲、乙两车从城出发前往城在整个行程中,汽车离开城的距离与行驶时间的对应关系如图所示.
(1)、求证:四边形是菱形;(2)、若 , , 求四边形的面积.24. 甲、乙两车从城出发前往城在整个行程中,汽车离开城的距离与行驶时间的对应关系如图所示. (1)、 ,两城相距千米,车先出发填甲或乙;(2)、分别求甲、乙两车在行驶过程中离开城的距离与行驶时间之间的函数解析式;(3)、在两车同时行驶过程中,当甲、乙两车相距时,求行驶时间的值.
(1)、 ,两城相距千米,车先出发填甲或乙;(2)、分别求甲、乙两车在行驶过程中离开城的距离与行驶时间之间的函数解析式;(3)、在两车同时行驶过程中,当甲、乙两车相距时,求行驶时间的值.
-