浙江省金华市义乌市后宅、佛堂、苏溪三校2023-2024学年九年级上学期数学10月月考试卷

试卷更新日期：2023-11-03 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列成语或词语所反映的事件中，可能性最小的是（）

A、瓜熟蒂落 B、旭日东升 C、夕阳西下 D、守株待兔

查看试题解析
2. 下列函数的图象，一定经过原点的是（）

A、 $y = x^{2} - 1$ B、 $y = 3 x^{2} - 2 x$ C、 $y = 2 x + 1$ D、 $y = \frac{2}{x}$

查看试题解析
3. 二次函数 $y = (x - 2)^{2} + 3$ 的最小值是（）

A、 $2$ B、 $3$ C、 $- 2$ D、 $- 3$

查看试题解析
4. 抛物线 $y = x^{2} - 2 x + 3$ 的顶点坐标是（）

A、 $(1 ， 3)$ B、 $(- 1 ， 3)$ C、 $(1 ， 2)$ D、 $(- 1 ， 2)$

查看试题解析
5. 把抛物线 $y = {(x - 1)}^{2} + 3$ 向上平移1个单位，再向右平移3个单位，得到的抛物线是（）

A、 $y = {(x + 2)}^{2} + 4$ B、 $y = {(x + 1)}^{2} + 2$ C、 $y = {(x - 4)}^{2} + 4$ D、 $y = {(x - 4)}^{2}$ +2

查看试题解析
6. 若二次函数 $y = a x^{2}$ 的图象经过点 $P (- 2 ， 4)$ ，则该图象必经过点（）

A、 $(2 ， 4)$ B、 $(- 2 ， - 4)$ C、 $(- 4 ， 2)$ D、 $(4 ， - 2)$

查看试题解析
7. 下列事件中，属于随机事件的是（）

A、 $13$ 名同学中至少有两名同学的生日在同一个月 B、在只有白球的盒子里摸到黑球 C、打开电视，正在播放动画片 D、用长为 $3 m$ 、 $5 m$ 、 $8 m$ 的三条线段能围成一个三角形

查看试题解析
8. 二次函数 $y = k x^{2} - 6 x + 3$ 的图象与x轴有交点，则k的取值范围是（）

A、 $k < 3$ B、 $k < 3$ 且 $k \neq 0$ C、 $k \leq 3$ D、 $k \leq 3$ 且 $k \neq 0$

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有下列4个结论：① $a b c > 0$ ；② $b^{2} > 4 a c$ ；③ $a (m^{2} - 1) + b (m - 1) < 0 (m \neq 1)$ ；④关于x的方程 $| a x^{2} + b x + c | = 1$ 有四个根，且这四个根的和为4，其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为 $a$ ， $b$ ， $c$ ，记 $p = \frac{a + b + c}{2}$ ，则其面积 $S = \sqrt{p (p - a) (p - b) (p - c)}$ ，这个公式也被称为海伦一秦九韶公式 $.$ 若 $p = 5$ ， $c = 2$ ，则此三角形面积的最大值为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{15}}{2}$ C、 $\sqrt{15}$ D、 $5$

查看试题解析

二、填空题（本大题共6小题，共24.0分）

11. 抛物线 $y = - x^{2} + 2 x + 3$ 与 $y$ 轴的交点坐标是.

查看试题解析
12. 在一个不透明的袋子中装有2个红球、5个白球和3个黑球，这些球除颜色外都相同.从中任意摸出1个球，摸到色的球的可能性最大.(填“红”、“白”或“黑”)

查看试题解析
13. 如图，若被击打的小球的飞行高度 $h ($ 单位： $m)$ 与飞行时间 $t ($ 单位： $s)$ 之间的关系为 $h = 35 t - 5 t^{2}$ ，则小球从飞出到落地所用时间为 $s .$

查看试题解析
14. 如图，甲、乙、丙 $3$ 人站在 $5 \times 5$ 网格中的三个格子中，小王随机站在剩下的空格中，与图中 $3$ 人均不在同一行或同一列的概率是．

查看试题解析
15. 如图，四边形 $O A B C$ 是边长为 $\sqrt{2}$ 的正方形， $O C$ 与 $x$ 轴正半轴的夹角为 $15 °$ ，点 $B$ 在抛物线 $y = a x^{2} (a < 0)$ 的图象上，则 $a$ 的值为．

查看试题解析
16. 如图，已知点 $A (3 ， 0)$ ， $B (1 ， 0)$ ，两点 $C (- 3 ， 9)$ ， $D (2 ， 4)$ 在抛物线 $y = x^{2}$ 上，向左或向右平移抛物线后， $C$ ， $D$ 的对应点分别为 $C'$ ， $D' .$ 当四边形 $A B C' D'$ 的周长最小时，抛物线的解析式为．

查看试题解析

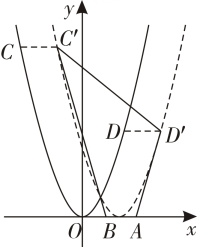
三、解答题（本大题共8小题，共66.0分。解答应写出文字说明，证明过程或演算步骤）

17. 已知抛物线 $y = x^{2} + b x + c$ 的图象经过 $A (- 1 ， 12)$ ， $B (0 ， 5)$ ．

(1)、求抛物线解析式和抛物线的顶点坐标．

(2)、当 $x$ 取什么范围时， $y$ 随着 $x$ 的增大而减小？

查看试题解析
18. 已知二次函数 $y = x^{2} - (m + 2) x + 2 m - 1$ ．

(1)、求证：不论 $m$ 取何值，该函数图象与 $x$ 轴总有两个公共点；

(2)、若该函数图象与 $y$ 轴交于点 $(0 ， 3)$ ，求该函数的图象与 $x$ 轴的交点坐标．

查看试题解析
19. 某校在课后服务中，成立了以下社团： $A .$ 计算机， $B .$ 围棋， $C .$ 篮球， $D .$ 书法每人只能加入一个社团，为了解学生参加社团的情况，从参加社团的学生中随机抽取了部分学生进行调查，并将调查结果绘制成如下两幅不完整的统计图，其中图 $1$ 中 $D$ 所占扇形的圆心角为 $150 °$ ．
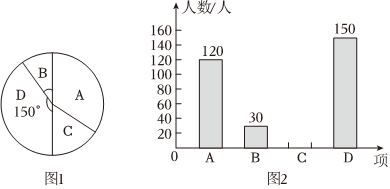
请结合图中所给信息解答下列问题：

(1)、这次被调查的学生共有人；

(2)、请你将条形统计图补充完整；

(3)、若该校共有 $1800$ 学生加入了社团，请你估计这 $1800$ 名学生中有多少人参加了篮球社团；

(4)、在书法社团活动中，由于甲、乙、丙、丁四人平时的表现优秀，恰好四位同学中有两名是男同学，两名是女同学 $.$ 现决定从这四人中任选两名参加全市书法大赛，用画树状图求恰好选中一男一女的概率．

查看试题解析
20. 如图，小亮父亲想用长 $80 m$ 的栅栏 $.$ 再借助房屋的外墙围成一个矩形的羊圈，已知房屋外墙长 $30 m$ ，设矩形 $A B C D$ 的边 $A B = x | m$ ，面积为 $S | m^{2}$ ．

(1)、写出 $S$ 与 $x$ 之间的函数表达式，并写出 $x$ 的取值范围；

(2)、当 $A B$ 为多少米时，羊圈的面积最大？最大值是多少？

查看试题解析
21. 如图，二次函数 $y = - x^{2} + (n - 1) x + 3$ 的图象与 $y$ 轴交于点 $A$ ，与 $x$ 轴的负半轴交于点 $B (- 2 ， 0)$ ．

(1)、求二次函数的解析式；

(2)、若点 $P$ 是这个二次函数图象在第二象限内的一点，过点 $P$ 作 $y$ 轴的垂线与线段 $A B$ 交于点 $C$ ，求线段 $P C$ 长度的最大值．

查看试题解析
22. 音乐喷泉 $($ 图 $1)$ 可以使喷水造型随音乐的节奏起伏变化而变化．某种音乐喷泉形状如抛物线，设其出水口为原点，出水口离岸边 $18 m$ ，音乐变化时，抛物线的顶点在直线 $y = k x$ 上变动，从而产生一组不同的抛物线 $($ 图 $2)$ ，这组抛物线的统一形式为 $y = a x^{2} + b x$ ．

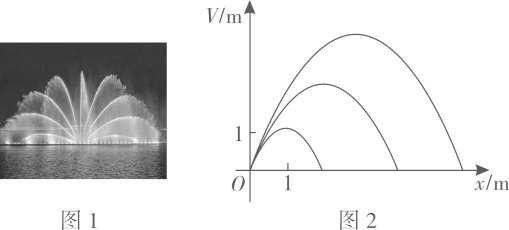(1)、若已知 $k = 1$ ，且喷出的抛物线水线最大高度达 $3 m$ ，求此时 $a$ 、 $b$ 的值；

(2)、若 $k = 1$ ，喷出的水恰好达到岸边，则此时喷出的抛物线水线最大高度是多少米？

(3)、若 $k = 3$ ， $a = - \frac{2}{7}$ ，则喷出的抛物线水线能否达到岸边？

查看试题解析
23. 定义：若一个函数图象上存在横、纵坐标相等的点，则称该点为这个函数图象的“等值点”，例如，点 $(2 ， 2)$ 是函数 $y = 2 x - 2$ 的图象的“等值点”．

(1)、分别判断函数 $y = \frac{5}{x} ， y = x + 2$ 的图象上是否存在“等值点”？如果存在，求出“等值点”的坐标；如果不存在，说明理由；

(2)、写出函数 $y = - x^{2} + 2$ 的等值点坐标；

(3)、若函数 $y = - x^{2} + 2 (x \leq m)$ 的图象记为 $W_{1}$ ，将其沿直线 $x = m$ 翻折后的图象记为 $W_{2}$ ．当 $W_{1} ， W_{2}$ 两部分组成的图象上恰有2个“等值点”时，请写出m的取值范围．

查看试题解析
24. 如图，抛物线 $y_{1} = a x^{2} + b x + c$ 的图象经过 $A (- 6 ， 0)$ ， $B (- 2 ， 0)$ ， $C (0 ， 6)$ 三点，且一次函数 $y = k x + 6$ 的图象经过点B.

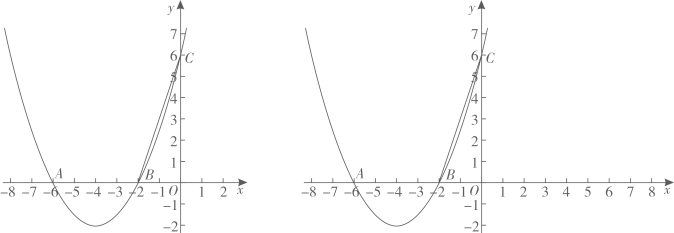(1)、求抛物线和一次函数的解析式.

(2)、点E，F为平面内两点，若以E、F、B、C为顶点的四边形是正方形，且点E在点F的左侧.这样的E，F两点是否存在？如果存在，请直接写出所有满足条件的点E的坐标：如果不存在，请说明理由.

(3)、将抛物线 $y_{1} = a x^{2} + b x + c$ 的图象向右平移8个单位长度得到抛物线 $y_{2}$ ，此抛物线的图象与x轴交于M，N两点（M点在N点左侧）.点P是抛物线 $y_{2}$ 上的一个动点且在直线 $N C$ 下方.已知点P的横坐标为m.过点P作 $P D ⊥ N C$ 于点D.求m为何值时， $C D + \frac{1}{2} P D$ 有最大值，最大值是多少？

查看试题解析