辽宁省丹东市2023年中考数学试卷
试卷更新日期:2023-11-03 类型:中考真卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
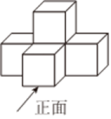
1. 的相反数是( )A、 B、 C、 D、2. 如图所示的几何体是由个完全相同的小立方块搭成,它的主视图是( )
 A、
A、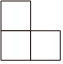 B、
B、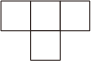 C、
C、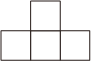 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 某校拟派一名跳高运动员参加一项校际比赛,对名跳高运动员进行了多次选拔比赛,他们比赛成绩的平均数和方差如下表:
3. 下列运算正确的是( )A、 B、 C、 D、4. 某校拟派一名跳高运动员参加一项校际比赛,对名跳高运动员进行了多次选拔比赛,他们比赛成绩的平均数和方差如下表:甲
乙
丙
丁
平均数
方差
根据表中数据,要从中选择一名平均成绩好,且发挥稳定的运动员参加比赛,最合适的人选是( )
A、甲 B、乙 C、丙 D、丁5. 如图所示,在中, , 垂足为点 , , 交于点若 , 则的度数是( )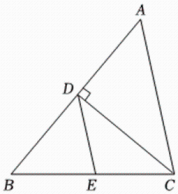 A、 B、 C、 D、6. 如图,直线过点 , , 则不等式的解集是( )
A、 B、 C、 D、6. 如图,直线过点 , , 则不等式的解集是( )
 A、 B、 C、 D、7. 在一个不透明的袋子中,装有个红球和若干个黑球,每个球除颜色外都相同,若从袋中任意摸出一个球是红球的概率为 , 则袋中黑球的个数为( )A、 B、 C、 D、8. 如图,在四边形中, , 以点为圆心,以任意长为半径作弧,分别交 , 于点 , , 分别以 , 为圆心,以大于长为半径作弧,两弧在内交于点 , 作射线 , 交于点 , 交的延长线于点若 , , 则的长为( )
A、 B、 C、 D、7. 在一个不透明的袋子中,装有个红球和若干个黑球,每个球除颜色外都相同,若从袋中任意摸出一个球是红球的概率为 , 则袋中黑球的个数为( )A、 B、 C、 D、8. 如图,在四边形中, , 以点为圆心,以任意长为半径作弧,分别交 , 于点 , , 分别以 , 为圆心,以大于长为半径作弧,两弧在内交于点 , 作射线 , 交于点 , 交的延长线于点若 , , 则的长为( )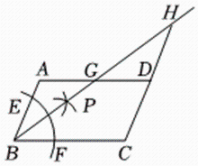 A、 B、 C、 D、9. 如图,在矩形中,对角线与相交于点 , , , 垂足为点 , 是的中点,连接 , 若 , 则矩形的周长是( )
A、 B、 C、 D、9. 如图,在矩形中,对角线与相交于点 , , , 垂足为点 , 是的中点,连接 , 若 , 则矩形的周长是( )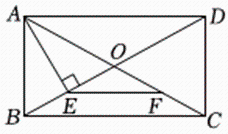 A、 B、 C、 D、10. 抛物线与轴的一个交点为 , 与轴交于点 , 点是抛物线的顶点,对称轴为直线 , 其部分图象如图所示,则以下个结论:; , 是抛物线上的两个点,若 , 且 , 则;在轴上有一动点 , 当的值最小时,则点的坐标为;若关于的方程无实数根,则的取值范围是其中正确的结论有( )
A、 B、 C、 D、10. 抛物线与轴的一个交点为 , 与轴交于点 , 点是抛物线的顶点,对称轴为直线 , 其部分图象如图所示,则以下个结论:; , 是抛物线上的两个点,若 , 且 , 则;在轴上有一动点 , 当的值最小时,则点的坐标为;若关于的方程无实数根,则的取值范围是其中正确的结论有( ) A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题(本大题共8小题,共24.0分)
-
11. 地球上的海洋面积约为 , 将数据用科学记数法表示为 .12. 因式分解: .13. 某青年排球队有名队员,年龄的情况如下表:
年龄岁
人数
则这名队员年龄的中位数是岁
14. 若代数式在实数范围内有意义,则实数的取值范围是 .15. 不等式组的解集是 .16. 如图,在正方形中, , 点 , 分别在边 , 上,与相交于点 , 若 , 则的长为 .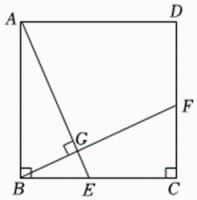 17. 如图,点是反比例函数的图象上一点,过点作轴,垂足为点 , 延长至点 , 使 , 点是轴上任意一点,连接 , , 若的面积是 , 则 .
17. 如图,点是反比例函数的图象上一点,过点作轴,垂足为点 , 延长至点 , 使 , 点是轴上任意一点,连接 , , 若的面积是 , 则 .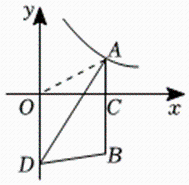 18. 如图,在平面直角坐标系中,点是坐标原点,已知点 , , 点在轴负半轴上,连接 , , 若 , 以为边作等边三角形 , 则点的坐标为;点的坐标为 .
18. 如图,在平面直角坐标系中,点是坐标原点,已知点 , , 点在轴负半轴上,连接 , , 若 , 以为边作等边三角形 , 则点的坐标为;点的坐标为 .
三、解答题(本大题共8小题,共96.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 先化简,再求值:
, 其中 .
20. 为提高学生的安全意识,某学校组织学生参加了“安全知识答题”活动该校随机抽取部分学生答题成绩进行统计,将成绩分为四个等级:优秀 , 良好 , 一般 , 不合格 , 并根据结果绘制成如图所示的两幅不完整的统计图.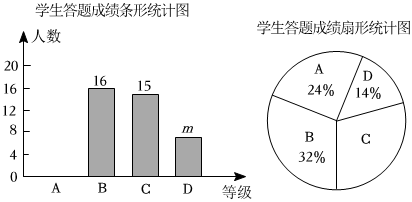
根据图中所给信息解答下列问题:
(1)、这次抽样调查共抽取人,条形统计图中的;(2)、将条形统计图补充完整,在扇形统计图中,求等所在扇形圆心角的度数;(3)、该校有名学生,估计该校学生答题成绩为等和等共有多少人;(4)、学校要从答题成绩为等且表达能力较强的甲、乙、丙、丁四名学生中,随机抽出两名学生去做“安全知识宣传员”,请用列表或画树状图的方法,求抽出的两名学生恰好是甲和丁的概率.21. “畅通交通,扮靓城市”,某市在道路提升改造中,将一座长度为米的桥梁进行重新改造为了尽快通车,某施工队在实际施工时,每天工作效率比原计划提高了 , 结果提前天成功地完成了大桥的改造任务,那么该施工队原计划每天改造多少米?22. 如图,已知是的直径,是的弦,点是外的一点, , 垂足为点 , 与相交于点 , 连接 , 且 , 延长交的延长线于点 .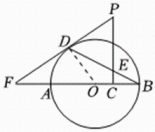 (1)、求证:是的切线;(2)、若 , , , 求的长.23. 一艘轮船由西向东航行,行驶到岛时,测得灯塔在它北偏东方向上,继续向东航行到达港,此时测得灯塔在它北偏西方向上,求轮船在航行过程中与灯塔的最短距离结果精确到参考数据: , , , , , .
(1)、求证:是的切线;(2)、若 , , , 求的长.23. 一艘轮船由西向东航行,行驶到岛时,测得灯塔在它北偏东方向上,继续向东航行到达港,此时测得灯塔在它北偏西方向上,求轮船在航行过程中与灯塔的最短距离结果精确到参考数据: , , , , , .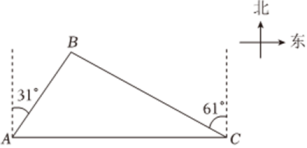 24. 某品牌大米远近闻名,深受广大消费者喜爱,某超市每天购进一批成本价为每千克元的该大米,以不低于成本价且不超过每千克元的价格销售当每千克售价为元时,每天售出大米;当每千克售价为元时,每天售出大米 , 通过分析销售数据发现:每天销售大米的数量与每千克售价元满足一次函数关系.(1)、请直接写出与的函数关系式;(2)、超市将该大米每千克售价定为多少元时,每天销售该大米的利润可达到元?(3)、当每千克售价定为多少元时,每天获利最大?最大利润为多少?25. 在中, , , , 点是的中点四边形是菱形按逆时针顺序排列 , , 且 , 菱形可以绕点旋转,连接和 , 设直线和直线所夹的锐角为 .
24. 某品牌大米远近闻名,深受广大消费者喜爱,某超市每天购进一批成本价为每千克元的该大米,以不低于成本价且不超过每千克元的价格销售当每千克售价为元时,每天售出大米;当每千克售价为元时,每天售出大米 , 通过分析销售数据发现:每天销售大米的数量与每千克售价元满足一次函数关系.(1)、请直接写出与的函数关系式;(2)、超市将该大米每千克售价定为多少元时,每天销售该大米的利润可达到元?(3)、当每千克售价定为多少元时,每天获利最大?最大利润为多少?25. 在中, , , , 点是的中点四边形是菱形按逆时针顺序排列 , , 且 , 菱形可以绕点旋转,连接和 , 设直线和直线所夹的锐角为 .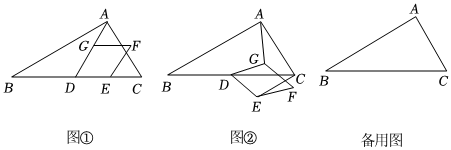 (1)、在菱形绕点旋转的过程中,当点在线段上时,如图 , 请直接写出与的数量关系及的值;(2)、当菱形绕点旋转到如图所示的位置时,中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、设直线与直线的交点为 , 在菱形绕点旋转一周的过程中,当所在的直线经过点时,请直接写出的面积.26. 抛物线与轴交于点 , , 与轴交于点 .
(1)、在菱形绕点旋转的过程中,当点在线段上时,如图 , 请直接写出与的数量关系及的值;(2)、当菱形绕点旋转到如图所示的位置时,中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、设直线与直线的交点为 , 在菱形绕点旋转一周的过程中,当所在的直线经过点时,请直接写出的面积.26. 抛物线与轴交于点 , , 与轴交于点 . (1)、求抛物线的表达式;(2)、如图,点是抛物线上的一个动点,设点的横坐标是 , 过点作直线轴,垂足为点 , 交直线于点当 , , 三点中一个点平分另外两点组成的线段时,求线段的长;(3)、若点是抛物线上的一个动点点不与顶点重合 , 点是抛物线对称轴上的一个点,点在坐标平面内,当四边形是矩形邻边之比为:时,请直接写出点的横坐标.
(1)、求抛物线的表达式;(2)、如图,点是抛物线上的一个动点,设点的横坐标是 , 过点作直线轴,垂足为点 , 交直线于点当 , , 三点中一个点平分另外两点组成的线段时,求线段的长;(3)、若点是抛物线上的一个动点点不与顶点重合 , 点是抛物线对称轴上的一个点,点在坐标平面内,当四边形是矩形邻边之比为:时,请直接写出点的横坐标.