吉林省长春市五十二教育集团2023-2024学年度九年级上学期数学第一次月考考试试卷

试卷更新日期：2023-11-03 类型：月考试卷

进入出卷网下载

一、选择题(本大题共8小题，每小题3分，共24分)

1. 下列各式中，能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{4}$ B、 $\sqrt{24}$ C、 $\sqrt{12}$ D、 $\sqrt{18}$

查看试题解析
2. 已知4a=5b(ab≠0)，下列变形错误的是（）

A、 $\frac{b}{4} = \frac{a}{5}$ B、 $\frac{a}{b} = \frac{5}{4}$ C、 $\frac{a}{b - a}$ =-5 D、 $\frac{b + 1}{4} = \frac{a + 1}{5}$

查看试题解析
3. 如图，在 $▱$ ABCD中，点E在CD上，EC：DC=1：3，连接AE交BD于点F．则△DEF与△BAF的周长之比为（）

A、4：9 B、1：3 C、1：2 D、2：3

查看试题解析
4. 关于x的一元二次方程x²-2x+m=0没有实数根，则m的值可能是（）

A、-2 B、0 C、1 D、2

查看试题解析
5. 如图，某飞机于空中A处探测到正下方的地面目标C，此时飞机高度AC为1200米，从飞机上看地面控制点B的俯角为 $α$ ，则B、C之间的距离为（）

A、 $\frac{1200}{t a n α}$ 米 B、 $1200 t a n α$ 米 C、 $1200 s i n α$ 米 D、 $1200 c o s α$ 米

查看试题解析
6. 如图，在平面直角坐标系中，等腰直角△A'B'C'是等腰直角△ABC以原点O为位似中心的位似图形。且位似比为2：1，点 A(1，0)， B(1，2)．C在A'B'上，则C'点坐标为（）

A、(2，4) B、(2，2) C、(4，2) D、(4，4)

查看试题解析
7. 果园2020年水果产量为50吨。2022 年水果产量为75吨。求该果园水果产量年平均增长率。设该果园水果产量的年平均增长率为x，则方程为（）

A、75(1-x)²=50 B、75(1+x)=50 C、50(1+x)²=75 D、50(1+x)=50

查看试题解析
8. 如图，在平面直角坐标系中，点A在第一象限。AB⊥y轴于点B，函数y= $\frac{k}{x}$ (x>0)的图象与线段AB交于点C，且AB=3BC．若△AOB的面积为12．则k的值为（）

A、4 B、6 C、8 D、12

查看试题解析

二、填空题(每小题3分，共18分)

9. 计算： $\sqrt{27} - \sqrt{3}$ =

查看试题解析
10. 计算cos60°+ sin30°=

查看试题解析
11. 若y=(m-1)x^m²+m是关于x的二次函数，则m的值为

查看试题解析
12. 如图，在平行四边形ABCD中，EF∥AB交AD于E．交BD于F，DE：EA=3：4，EF=3．则CD的长为

查看试题解析
13. 如图，在 $5 \times 4$ 的正方形网格中，每个小正方形的边长都是1， $△ A B C$ 的顶点都在这些小正方形的顶点上，则 $\sin ∠ B A C$ 的值为．

查看试题解析
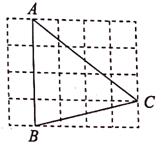14. 如图。在Rt△ABO中，∠OBA=90°，A(4，4)，点C在边AB上。且 $\frac{A C}{C B} = \frac{1}{3}$ ，点D为OB的中点，点P为边OA上的动点，当点P在OA上移动时，使四边形PDBC周长最小的点P的纵坐标为

查看试题解析

三、解答题(本大题共10小题，共78分)

15. 先化简。再求值： (a+1)²-(a+3)(a-3)．其中a= $\frac{5}{2}$

查看试题解析
16. 某小区某天在厂场设置了A、B、C三个核酸检测通道，甲、乙两人这天均随机选择这三条通道中的一条进行核酸检测。用画树状图(或列表)的方法，求甲、乙两人这天在同一个检测通道进行核酸检测的概率．

查看试题解析
17. 按照疫情防控的要求，某校计划在学生返校前对学校60个相同大小的教室进行全面清扫和消毒，在实际进行消毒时，每天消毒的教室数量是原计划的1.2倍，使得完成全部教室消毒的时间缩短了2天.求原计划每天可以清扫和消毒的教室个数.

查看试题解析
18. 图①、图②、图③均是8×8的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1．点A、B、C均在格点上。在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，不要求写出画法，保留作图痕迹。

(1)、在图①中画出△ABC的中线BD．

(2)、在图②△ABC的边AB上找到一点E，将AB分成2：3两部分．

(3)、在图③△ABC的边BC上找到一点F．使S_△A_DF：S_△A_EF=2：3．

查看试题解析
19. 新冠肺炎疫情期间，我国各地采取了多种方式进行预防．其中。某地运用无人机规劝居民回家，如图，无人机于空中A处测得某建筑部B处的仰角为45°．测符该建筑底部C处的俯角为17°，若无人机的飞行高度AD为10m，求该建筑BC的高度(结果取整数)．
参考数据：sin 17°≈0.29， cos17°≈0.96，tan17°≈0.31．

查看试题解析
20. 如图，在△ABC中，AD⊥BC，交边BC于点D，点E为边AC的中点。过点A作AF∥BC，交DE的延长线于点F，连结CF．

(1)、求证：四边形ADCF是矩形：

(2)、若BC=DF．且tanB= $\frac{3}{2}$ ，则 $\frac{S_{△ A B C}}{S_{矩形 A F B C}}$ =

查看试题解析
21. 为弘扬中华传统文化，草根一中准备开展“传统手工技艺”学习实践活动．校学生会在全校范围内随机地对本校一些学生进行了“我最想学习的传统手工技艺"问卷调查(问卷共没有五个选项：“A-剪纸”、“B-木版画雕刻”，"C-陶艺创作”、"D-皮影制作”、 “E-其他手工技艺”。参加问卷调查的这些学生，每人都只选了其中的一个选项)。将所有的调有结果绘制成如下两幅不完整的统计图：
请你根据以上信息，回答下列问题：．

(1)、补全上面的条形统计图

(2)、本次问卷的这五个选项中。众数是

(3)、该校共有3600名学生，请你估计该校学生“最也学习的传统手工技艺”为“A-剪纸”的人数，

查看试题解析
22. 某食品加工厂的甲、乙两个生产组领到了相同的加工任务，甲，乙两组以相同的工作效率同时开始工作。中途乙组因升级设备，停工了一段时间．乙组设备升级完毕后，提高了工作效率，在完成本组任务后，并帮组甲组加工了60 kg食品，最后两组同时停工，完成了此次加工任务．两组各自加工的食品量y (kg) 与中组工作时间x (h) 之间的函数图象如图所示，

(1)、甲组每小时加工食品kg．乙组升级设备后每小时加工食品 kg

(2)、求乙组设备升级完成后y与x之间的函数关系式

(3)、求m、n的值．

查看试题解析
23. 实践与探究

(1)、操作一：如图①．已知正方形纸片ABCD，将正方形纸片沿过点A的直线折叠，使点B落在正方形ABCD的内部，点B的对应点为点M，折痕为AE．再将纸片沿过点A的直线折叠，使AD与AM重合，折痕为AF．则∠EAF=度．

(2)、操作二：如图②，将正方形纸片沿EF继续折叠，点C的对应点为点N．当点N恰好落在折痕AE上，则∠AEF= 度．

(3)、在图②中，运用以上操作所得结论，解答下列问题：
①设AM与NF的交点为点P．求证：AP=EF：
②若AB= $4 \sqrt{3}$ ，则线段EF的长为

查看试题解析
24. 如图，在△ABC中，tanB= $\frac{1}{2}$ ， ∠C=45°，AD=6，AD⊥BC于点D，动点E从点D出发沿DB向点B以每秒1个单位长度的速度运动，将线段DE绕点D顺时针旋转90°，得到线段DF，过点F作FG∥AC，交射线DC于点G．以EC、FC为邻边 $▱$ EGFP． $▱$ EGFP与△ABC重叠部分面积为S．当点E与点B重合时停止运动，设点E的运动时间为t秒(t>0) ．

(1)、求BC的长，

(2)、出点P落到AB边上时，求t的值．

(3)、当点F在线段AD上时，求S与t之间的函数关系式.

(4)、 $▱$ EGFP的边PE被AB分成1：3两部分时，直接写出t的值。

查看试题解析