期中微专题提分精炼：相似三角形的性质-2023-2024学年北师大版九年级（上）数学

试卷更新日期：2023-11-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 若 $△ A B C ∽ △ D E F$ ，其相似比为 $2 ： 3$ ，则 $△ A B C$ 与 $△ D E F$ 的面积比为（）

A、 $2 ： 3$ B、 $3 ： 2$ C、 $4 ： 9$ D、 $16 ： 81$

查看试题解析
2. $△ A B C$ 的三边长分别为2，3，4，另有一个与它相似的三角形 $△ D E F$ ，其最长边为16，则 $△ D E F$ 的周长是（）

A、54 B、36 C、27 D、21

查看试题解析
3. 若两个相似三角形的面积之比为1：4，则它们的最长边的比是（）

A、1：2 B、1：4 C、1：16 D、无法确定

查看试题解析
4. 如图所示， $△ A B C ∽ △ D E F$ ，则 $∠ D$ 的度数为（）

A、 $35 °$ B、 $45 °$ C、 $65 °$ D、 $80 °$

查看试题解析
5. 如图，已知△ADE和△ABC的相似比是1：2，且△ADE的面积为2，则四边形DBCE的面积是（）

A、8 B、6 C、4 D、2

查看试题解析
6. 如图， $△ A B C$ 与 $△ D E F$ 是位似图形，点 $O$ 为位似中心，已知 $B O ： O E = 2 ： 1$ ，则 $△ A B C$ 与 $△ D E F$ 的面积比是（）

A、2：1 B、3：1 C、4：1 D、5：1

查看试题解析
7. 如图，在 $A B C$ 纸板中， $A C = 4$ ， $B C = 8$ ， $A B = 11$ ， $P$ 是 $B C$ 上一点，沿过点 $P$ 的直线剪下一个与 $△ A B C$ 相似的小三角形纸板．针对 $C P$ 的不同取值，三人的说法如下．下列判断正确的是（）

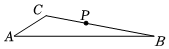
甲：若 $C P = 4$ ，则有 $3$ 种不同的剪法；

乙：若 $C P = 2$ ，则有 $4$ 种不同的剪法；

丙：若 $C P = 1$ ，则有 $3$ 种不同的剪法．

A、乙错，丙对 B、甲和乙都错 C、乙对，丙错 D、甲错，丙对

查看试题解析
8. 已知 $△ A B C$ 的三边长分别为 $6 c m$ ， $7.5 c m$ ， $9 c m$ ， $△ D E F$ 的一边长为 $5 c m$ ，如果这两个三角形相似，那么 $△ D E F$ 的另两边长可能是（）

A、 $2 c m$ ， $3 c m$ B、 $4 c m$ ， $6 c m$ C、 $6 c m$ ， $7 c m$ D、 $6 c m$ ， $8 c m$

查看试题解析
9. 要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为 $5 c m$ ， $10 c m$ 和 $12 c m$ ，另一个三角形的最短边长为 $2.5 c m$ ，则它的最长边为（）

A、 $3 c m$ B、 $5 c m$ C、 $6 c m$ D、 $6.5 c m$

查看试题解析
10. 已知，△ABC∽△A′B′C′，且△A′B′C′的面积为6，△A′B′C′周长是△ABC的周长的 $\frac{1}{2}$ ， AB＝8，则AB边上的高等于（）

A、3 B、6 C、9 D、12

查看试题解析

二、填空题

11. 若两个相似三角形的周长比是4：9，则对应角平分线的比是．

查看试题解析
12. 已知 $△ A B C$ 与 $△ D E F$ 相似，且点A与点 $D$ 是对应点，点 $B$ 与点 $E$ 是对应点，如果 $∠ A = 50 °$ ， $∠ B = 60 °$ ，那么 $∠ F =$ ．

查看试题解析
13. 若两个相似三角形的一组对应边长分别为16和32，它们的周长之差为36，则较小三角形的周长是.

查看试题解析
14. 如果两个相似三角形的面积之比是4：25，其中小三角形最大内角的角平分线长是12cm，那么大三角形最大内角的角平分线长是cm．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ C = 90 ° ， A C = 10 c m ， B C = 8 c m$ .点P从点C出发，以 $2 c m / s$ 的速沿着 $C A$ 向点A匀速运动，同时点Q从点B出发，以 $1 c m / s$ 的速度沿 $B C$ 向点C匀速运动，当一个点到终点时，另一个点随之停止.经过秒后， $△ P C Q$ 与 $△ A B C$ 相似.

查看试题解析

三、解答题

16. 如图，在△ABC中，AB＝10cm，BC＝20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果点P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．

查看试题解析
17. 如图， $A B ⊥ B D ， C D ⊥ B D ， A B = 6 ， C D = 4 ， B D = 14$ ，点P在 $B D$ 上移动，当以P，C，D为顶点的三角形与 $△ A B P$ 相似时，求 $B P$ 的长.

查看试题解析
18. 如图，已知 $△ A B D ∽ △ A C E$ ， $∠ A B C = 50^{\circ}$ ， $∠ B A C = 60^{\circ}$ ，求 $∠ A E D$ 的度数．

查看试题解析
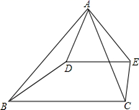19. 如图，在△ABC中，点D是AB的中点，DE∥BC交AC于点E，DF∥BE交AC于点F，若EF＝3，求AC的长.

查看试题解析
20. 已知 $Δ A B C$ 和 $Δ D E F$ 中，有 $\frac{A B}{D E} = \frac{B C}{E F} = \frac{C A}{F D} = \frac{2}{3}$ ,且 $Δ A B C$ 和 $Δ D E F$ 的周长之差为15厘米，求 $Δ A B C$ 和 $Δ D E F$ 的周长.

查看试题解析

四、综合题

21. 如图，一块三角形材料ABC中， $∠ C = 90 °$ ， $\sin A = \frac{1}{3}$ ， $A B = 9$ cm，用这块材料剪出一个矩形CDEF，其中点D，E，F分别在BC，AB，AC上．

(1)、若EF的长度为xcm，则 $A F =$ cm；（用含x的代数式表示）

(2)、要使剪出的矩形CDEP的面积最大，则矩形的长、宽分别是多少？

查看试题解析
22. 请阅读以下材料，并完成相应的问题：
角平分线分线段成比例定理，如图1，在△ABC中，AD平分∠BAC，则 $\frac{A B}{A C} = \frac{B D}{C D}$ ．
下面是这个定理的部分证明过程．
证明：如图2，过点C作 $C E ∥ D A$ ．交BA的延长线于点E．…

(1)、任务：
请按照上面的证明思路，写出该证明过程的剩余部分；

(2)、如图3，已知Rt△ABC中，AB＝3，BC＝4，∠ABC＝90°，AD平分∠BAC，求△ABD的周长．

查看试题解析
23. 如图，在正方形ABCD中，E，F分别是边AD，CD上的点，AE＝ED，DF＝ $\frac{1}{3}$ FC，连结EF交BC的延长线于点G．

(1)、试说明：△ABE∽△DEF；

(2)、若正方形的边长为4，求BG的长．

查看试题解析
24. 如图，在 $△ A B C$ 中点D，E，F分别在 $A B$ ， $B C$ ， $A C$ 边上， $D E // A C$ ， $E F // A B$ .

(1)、求证： $△ B D E \sim △ E F C$ ；

(2)、若 $\frac{A F}{F C} = \frac{1}{2}$ ， $△ E F C$ 的面积是20，求 $△ A B C$ 的面积.

查看试题解析
25. 如图，Rt△ABC，∠C＝90°，AC＝10cm，BC＝8cm．点P从点C出发，以2cm/s的速度沿CA向点A匀速运动，同时点Q从点B出发，以1cm/s的速度沿BC向点C匀速运动，当一个点到达终点时，另一个点随之停止．

(1)、求经过几秒后，△PCQ的面积等于△ABC面积的 $\frac{2}{5}$ ？

(2)、经过几秒，△PCQ与△ABC相似？

查看试题解析