期中微专题提分精炼:相似三角形判定定理的证明-2023-2024学年北师大版九年级(上)数学
试卷更新日期:2023-11-02 类型:复习试卷
一、选择题
-
1. 如图,D、E分别是△ABC边AB、AC上的点,DE∥BC,且AD:BD=1:2,那么S△ADE:S△ABC的值为( )
 A、1:4 B、1:6 C、1:8 D、1:92. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A、1:4 B、1:6 C、1:8 D、1:92. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( ) A、
A、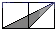 B、
B、 C、
C、 D、
D、 3. 在物理课中同学们曾学过小孔成像:在较暗的屋子里,把一支点燃的蜡烛放在一块半透明的塑料薄膜前面,在它们之间数一块钻有小孔章的纸板,由于光沿直线传播,塑料薄膜上就出现了蜡烛火焰倒立的像(如图1),这种现象就是小孔成像,在图2中,如果蜡烛火焰图1根B到孔О的距离为 , 火焰根的像到孔O的距离为10cm,蜡烛火焰的高度为 , 那么倒立的像的高度为( )
3. 在物理课中同学们曾学过小孔成像:在较暗的屋子里,把一支点燃的蜡烛放在一块半透明的塑料薄膜前面,在它们之间数一块钻有小孔章的纸板,由于光沿直线传播,塑料薄膜上就出现了蜡烛火焰倒立的像(如图1),这种现象就是小孔成像,在图2中,如果蜡烛火焰图1根B到孔О的距离为 , 火焰根的像到孔O的距离为10cm,蜡烛火焰的高度为 , 那么倒立的像的高度为( ) A、 B、 C、 D、4. 如图,在 中, , ,若 的周长为 ,则 的周长是( )
A、 B、 C、 D、4. 如图,在 中, , ,若 的周长为 ,则 的周长是( )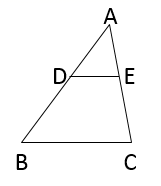 A、 B、 C、 D、5. 如图,在中,点 , , 分别是 , , 的中点.若的面积为 , 则的面积为( )
A、 B、 C、 D、5. 如图,在中,点 , , 分别是 , , 的中点.若的面积为 , 则的面积为( ) A、 B、 C、2 D、46. 图1是伸缩折叠不锈钢晾衣架的实物图,图2是它的侧面示意图,和相交于点O,点A,B之间的距离为1.2米, , 根据图2中的数据可得点C,D之间的距离为( )
A、 B、 C、2 D、46. 图1是伸缩折叠不锈钢晾衣架的实物图,图2是它的侧面示意图,和相交于点O,点A,B之间的距离为1.2米, , 根据图2中的数据可得点C,D之间的距离为( ) A、0.8米 B、0.86米 C、0.96米 D、1米7. 如图,中,E是延长线上一点,交于点F,且 , , 则( )
A、0.8米 B、0.86米 C、0.96米 D、1米7. 如图,中,E是延长线上一点,交于点F,且 , , 则( ) A、2 B、3 C、4 D、68. 已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
A、2 B、3 C、4 D、68. 已知△ABC如图,则下列4个三角形中,与△ABC相似的是( ) A、
A、 B、
B、 C、
C、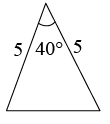 D、
D、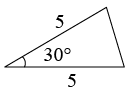 9. 如图,已知D是中的边上的一点, , 的平分线交边于E,交于F,那么下列结论中错误的是( )
9. 如图,已知D是中的边上的一点, , 的平分线交边于E,交于F,那么下列结论中错误的是( ) A、△BAC∽△BDA B、△BFA∽△BEC C、△BDF∽△BEC D、△BDF∽△BAE10. 如图,在四边形中, , , E,F分别是 , 的中点,连接 , , , 点P为边上一点,过点P作 , 交于点Q,若 , 则的长为( )
A、△BAC∽△BDA B、△BFA∽△BEC C、△BDF∽△BEC D、△BDF∽△BAE10. 如图,在四边形中, , , E,F分别是 , 的中点,连接 , , , 点P为边上一点,过点P作 , 交于点Q,若 , 则的长为( ) A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
11. 如图,点D是等边△ABC边AB上的一点,且AD:DB=2:3,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF= .
 12. 如图,在中, , , 平分 , 若 , 则的长为 .
12. 如图,在中, , , 平分 , 若 , 则的长为 . 13. 如图,在矩形中,点E,点F分别是边和边的中点,于点M,连接 , 下列四个结论:①;②;③;④ , 其中正确的结论有 . (只填写序号即可)
13. 如图,在矩形中,点E,点F分别是边和边的中点,于点M,连接 , 下列四个结论:①;②;③;④ , 其中正确的结论有 . (只填写序号即可) 14. 如图,点D在边上, , , , 点E、F分别在边、上,连接 , 将沿着翻折,点E恰好与点F重合,则的长等于 .
14. 如图,点D在边上, , , , 点E、F分别在边、上,连接 , 将沿着翻折,点E恰好与点F重合,则的长等于 . 15. 如果梯形的一条对角线把梯形分成的两个三角形相似,那么我们称该梯形为“优美梯形”.如果一个直角梯形是“优美梯形”,它的上底等于2,下底等于4,那么它的周长为 .
15. 如果梯形的一条对角线把梯形分成的两个三角形相似,那么我们称该梯形为“优美梯形”.如果一个直角梯形是“优美梯形”,它的上底等于2,下底等于4,那么它的周长为 .三、解答题
-
16. 从三角形不是等腰三角形的一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中,一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
 (1)、如图 , 在中,为角平分线, , , 求证:为的完美分割线;(2)、在中, , 是的完美分割线,且为等腰三角形,求的度数;(3)、如图 , 在中, , , 是的完美分割线,且是以为底边的等腰三角形,求完美分割线的长.17. 如图,BD、AC相交于点P,连接BC、AD,且∠1=∠2,若PB=3,PC=1,PD=2,求PA的长度.
(1)、如图 , 在中,为角平分线, , , 求证:为的完美分割线;(2)、在中, , 是的完美分割线,且为等腰三角形,求的度数;(3)、如图 , 在中, , , 是的完美分割线,且是以为底边的等腰三角形,求完美分割线的长.17. 如图,BD、AC相交于点P,连接BC、AD,且∠1=∠2,若PB=3,PC=1,PD=2,求PA的长度. 18. 如图,在中, , D,E分别为边上的点, , 当时,求的长.
18. 如图,在中, , D,E分别为边上的点, , 当时,求的长.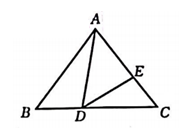 19. 如图,在平行四边形ABCD中,点E在边BC上,连结AE并延长,交对角线BD于点F、DC的延长线于点G.如果 , 求的值.
19. 如图,在平行四边形ABCD中,点E在边BC上,连结AE并延长,交对角线BD于点F、DC的延长线于点G.如果 , 求的值. 20. 如图,在矩形ABCD中,点E、F分别在边AD、DC上,BE⊥EF,AB=6,AE=9,DE=2,求EF的长.
20. 如图,在矩形ABCD中,点E、F分别在边AD、DC上,BE⊥EF,AB=6,AE=9,DE=2,求EF的长.
四、综合题
-
21. 如图(1)所示,在中, , D是上一点(不与A,B重合), , 交于点E,连结.设的面积为S,的面积为.
 (1)、当时,的面积是6,求的面积的值;(2)、当时,求S值(结果用含字母的代数式表示);(3)、如图(2)所示,在四边形中, , E是上一点(不与A,B重合), , 交于点F,连结.设 , 四边形的面积为S,的面积为 , 请你利用前面问题的解法或结论,用含字母n的代数式表示.22. 已知:如图,在四边形中,平分 , .
(1)、当时,的面积是6,求的面积的值;(2)、当时,求S值(结果用含字母的代数式表示);(3)、如图(2)所示,在四边形中, , E是上一点(不与A,B重合), , 交于点F,连结.设 , 四边形的面积为S,的面积为 , 请你利用前面问题的解法或结论,用含字母n的代数式表示.22. 已知:如图,在四边形中,平分 , . (1)、尺规作图:在上求作一点E,使得.(保留作图痕迹,不写作法)(2)、若 , ,
(1)、尺规作图:在上求作一点E,使得.(保留作图痕迹,不写作法)(2)、若 , ,①求的长;
②在(1)的条件下,连接交于点F,求的值.
23. 已知:E是矩形的边上一个动点,直线交于点F, (1)、求证:;(2)、若直线经过C点,且 , 是否存在这样的点E,使和相似?若存在,请求出的长度;若不存在,请说明理由.(3)、连结 , 若 , 当和相似时,则.
(1)、求证:;(2)、若直线经过C点,且 , 是否存在这样的点E,使和相似?若存在,请求出的长度;若不存在,请说明理由.(3)、连结 , 若 , 当和相似时,则.

