期中微专题提分精炼：探索三角形相似的条件-2023-2024学年北师大版九年级（上）数学

试卷更新日期：2023-11-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图示，已知 $∠ 1 = ∠ 2$ ，那么添加下列一个条件后，仍无法判定 $△ A B C ∽ △ A D E$ 的是（　　）

A、 $∠ D = ∠ B$ B、 $∠ C = ∠ A E D$ C、 $\frac{A B}{A D} = \frac{A C}{A E}$ D、 $\frac{A B}{A D} = \frac{B C}{D E}$

查看试题解析
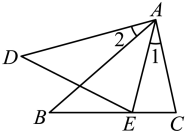2. 下列两个三角形不一定相似的是（）．

A、有一个内角是 $50 °$ 的两个直角三角形 B、有一个内角是 $50 °$ 的两个等腰三角形 C、两条直角边的比都是 $2 ： 3$ 的两个直角三角形 D、腰与底的比都是 $2 ： 3$ 的两个等腰三角形

查看试题解析
3. 如图，在△ABC中，点D、E分别在边AB、AC上，下列条件不能满足△ADE∽△ACB的条件是（）

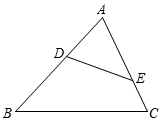A、∠AED=∠B B、 $\frac{A D}{A C} = \frac{A E}{A B}$ C、AD·BC= DE·AC D、DE//BC

查看试题解析
4. 下列命题正确的是（）

A、任意两个矩形一定相似 B、如果C点是线段AB的黄金分割点，那么 $\frac{A C}{A B} = \frac{\sqrt{5} - 1}{2}$ C、相似图形就是位似图形 D、有一个锐角相等的两个直角三角形相似

查看试题解析
5. 如图， $D$ 是 $△ A B C$ 边 $A B$ 上一点，添加一个条件后，仍不能使 $△ A C D ∽ △ A B C$ 的是（）

A、 $∠ A C D = ∠ B$ B、 $∠ A D C = ∠ A C B$ C、 $A C^{2} = A D \cdot A B$ D、 $\frac{A D}{A C} = \frac{C D}{B C}$

查看试题解析
6. 古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 $\frac{\sqrt{5} - 1}{2}$ （ $\frac{\sqrt{5} - 1}{2} \approx 0.618$ ，称为黄金分割比例），著名的“断臂维纳斯”便是如此.若小凡的身高满足此黄金分割比例，且肚脐至足底的长度为 $108 cm$ ，则小凡的身高约为（）

A、 $155 cm$ B、 $165 cm$ C、 $175 cm$ D、 $185 cm$

查看试题解析
7. 若点C是线段AB的黄金分割点（AC＞BC），AB＝2，则AC的长为（）

A、 $\sqrt{5} - 1$ B、 $\frac{3 - \sqrt{5}}{2}$ C、 $3 - \sqrt{5}$ D、 $\frac{\sqrt{5} - 1}{2}$

查看试题解析
8. 已知在 $△ A B C$ 中， $∠ A = 78 ° ， A B = 4 ， A C = 6$ ，则下列选项中阴影部分的三角形与原 $△ A B C$ 不相似的是（　　）

A、 B、 C、 D、

查看试题解析
9. 一个钢筋三脚架三边长分别为 $30 c m ， 60 c m ， 80 c m$ ，现在要做一个和它相似的钢筋三脚架，而只有长为 $40 c m$ 和 $90 c m$ 的两根钢筋，要求以其中的一根为一边，从另一根上截两段（允许有余料）作为另两边，则不同的截法有（　　）

A、一种 B、两种 C、三种 D、四种或四种以上

查看试题解析
10. 一本书的宽与长之比为黄金比，书的宽为14cm，则它的长为（　　）cm

A、 $7 \sqrt{5} + 7$ B、 $21 - 7 \sqrt{5}$ C、 $7 \sqrt{5} - 7$ D、 $7 \sqrt{5} - 21$

查看试题解析

二、填空题

11. 点 $P$ 在线段 $A B$ 上，且 $B P^{2} = A P \cdot A B$ ， $A B = 6$ ，那么 $B P$ 的长为．

查看试题解析
12. 比值为 $\frac{\sqrt{5} - 1}{2}$ （约为0.618）的比例被公认为是最能引起美感的比例，因此被称为黄金分割比，电视机屏幕的宽与长之比就非常接近这个比例．如果某款电视机屏幕的长为90厘米，则其宽约为厘米．（精确到1厘米）

查看试题解析
13. 符合黄金分割比例 $(\frac{\sqrt{5} - 1}{2})$ 形式的图形很容易使人产生视觉上的美感。在如图所示的五角星中， $A D = B C = \frac{\sqrt{5} + 1}{2}$ ，且C，D两点都是 $A B$ 的黄金分割点，则 $C D$ 的长为．

查看试题解析
14. 如图，在正方形网格中有三个三角形，分别是 $△ E B C$ ， $△ C D B$ ， $△ D E B$ ，其中与 $△ A B C$ 相似的是．

查看试题解析
15. 如图，在四边形 $A B C D$ 中 $∠ B A C = ∠ A D C = 90 °$ ，添加一个条件，可以利用定理“斜边和直角边对应成比例，两个直角三角形相似”证明 $R t △ D C A ∽ R t △ A B C$ ．

查看试题解析

三、解答题

16. 如图，在边长为4的正方形ABCD中，P是BC上的点，且BP＝3PC，Q是CD的中点，求证：△ADQ∽△QCP．

查看试题解析
17. 如图，在平行四边形 $A B C D$ 中，E为 $A B$ 边上一点，连接 $C E$ ， F为 $C E$ 上一点，且 $∠ D F C = ∠ B$ ．求证： $△ D C F ∽ △ C E B$ ．

查看试题解析
18. 如图，已知∠1=∠2，∠AED=∠C，
求证：△ABC∽△ADE

查看试题解析
19. 如图，在矩形ABCD中，AB＝6，BC＝8，沿直线MN对折，使A、C重合，直线MN交AC于O．求证：△COM∽△CBA．

查看试题解析
20. 如图，已知 $∠ B A C = ∠ E A D$ ， $A B = 24$ ， $A C = 48$ ， $A E = 17$ ， $A D = 34$ ，求证： $△ A B C ∽ △ A E D$ ．

查看试题解析

四、综合题

21. 如图，在△ABC中，D、E分别是边AC、BC的中点，F是BC延长线上一点，∠F＝∠B．

(1)、若AB＝10，求FD的长；

(2)、若AC＝BC，求证：△CDE∽△DFE．

查看试题解析
22. 如图，将一个 $R t △ B P E$ 与正方形 $A B C D$ 叠放在一起，并使其直角顶点P落在线段 $C D$ 上（不与C，D两点重合），斜边的一部分与线段 $A B$ 重合．

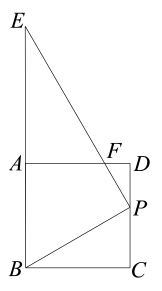(1)、图中与 $R t △ B C P$ 相似的三角形共有个，分别是；

(2)、请选择第（1）问答案中的任意一个三角形，完成该三角形与 $△ B C P$ 相似的证明．

查看试题解析
23. 如图，在 $△$ ABC中，AB=AC，∠A为锐角且不等于60°，AD平分∠BAC交BC于点D，BE⊥AC于点E，AD交BE于点F．

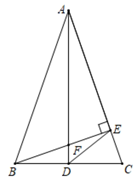(1)、写出图中所有与 $△$ ACD相似的三角形（全等除外）；

(2)、连接DE，求证： $△$ ABF∽△EDF．

查看试题解析
24.

(1)、已知a＝4.5，b＝2，c是a，b的比例中项，求c；

(2)、如图，C是AB的黄金分割点，且AC＞BC，AB＝4，求AC的长．

查看试题解析
25. 如图，在Rt△ABC中，∠C＝90°，AC=10cm，BC＝8cm．点M从点C出发，以2cm/s的速度沿CA向点A匀速运动，点N从点B出发，以1cm/s的速度沿BC向点C匀速运动，当一个点到达终点时，另一点也随即停止运动．

(1)、经过几秒后，△MCN的面积等于△ABC面积的 $\frac{2}{5}$ ？

(2)、经过几秒，△MCN与△ABC相似？

查看试题解析