期中微专题提分精炼：平行线分线段成比例-2023-2024学年北师大版九年级（上）数学

试卷更新日期：2023-11-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 在 $△ A B C$ 中，点D、E分别在边 $A B$ 、 $A C$ 上，如果 $A D ： B D = 1 ： 2$ ，下列条件中，能判断 $D E ∥ B C$ 的是（）．

A、 $D E ： B C = 1 ： 2$ B、 $D E ： B C = 1 ： 3$ C、 $A E ： A C = 1 ： 2$ D、 $A E ： A C = 1 ： 3$

查看试题解析
2. 已知线段a、b、c，作线段x，使 $a ： b = c ： x$ ，下列每个图的两条虚线都是平行线，则正确的作法是（　　）

A、 B、 C、 D、

查看试题解析
3. 如图： $A B ∥ C D ∥ E F$ ， $A D ： D F = 3 ： 1 ， B E 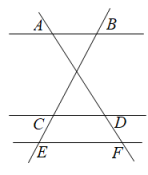= 12$ ，那么CE的长为（）

A、3 B、4 C、5 D、6

查看试题解析
4. 如图，l₁ ， l₂ ， l₃ ， l₄是一组平行线，l₅ ， l₆与这组平行线依次相交于点A，B，C，D和E，F，G，H．若AB∶BC∶CD=2∶3∶4，EG=10，则EH的长为（）

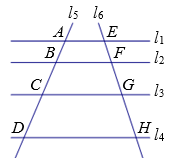A、14 B、16 C、18 D、20

查看试题解析
5. 如图，在 $△ A B C$ 中，点D，E分别在 $A B$ ， $A C$ 上，且 $D E ∥ B C$ ，下列式子不成立的是（）

A、 $\frac{A D}{D B} = \frac{A E}{E C}$ B、 $\frac{A B}{D B} = \frac{A C}{E C}$ C、 $\frac{A B}{A D} = \frac{A C}{A E}$ D、 $\frac{A B}{A D} = \frac{A E}{A C}$

查看试题解析
6. 如图，DE∥BC，DF∥AC，则下列比例式中正确的是（）

A、 $\frac{A E}{E C} = \frac{D F}{B C}$ B、 $\frac{A E}{E C} = \frac{C F}{F B}$ C、 $\frac{D E}{B C} = \frac{D F}{A C}$ D、 $\frac{F C}{B C} = \frac{E C}{A C}$

查看试题解析
7. 如图，四边形 $A B C D$ 为菱形， $A C ， B D$ 相交于点O，E是 $O A$ 的中点，连接 $B E$ 并延长交 $A D$ 于点F．已知 $B E = 4$ ，则 $E F$ 的长为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{3}{2}$ D、 $\frac{4}{3}$

查看试题解析
8. 如图，△ABC中，D、E、F三点分别在AB、AC、BC边上，且有DE∥BC，EF∥AB，AD＝2BD，则 $\frac{C F}{C B} =$ （）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
9. 如图，矩形纸片 $A B C D$ 中， $A D = 9$ ， $E$ 是 $C D$ 上一点，连结 $A E$ ， $Δ A D E$ 沿直线 $A E$ 翻折后点 $D$ 落到点 $F$ ，过点 $F$ 作 $F G ⊥ A D$ ，垂足为 $G$ ．若 $A G = 2 G D$ ，则 $D E$ 的值为（）

A、 $3 \sqrt{3}$ B、 $\frac{9}{2}$ C、5 D、 $\frac{9}{5} \sqrt{5}$

查看试题解析
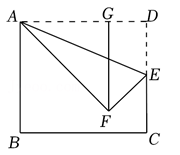10. 如图，正方形 ABCD中AB= 3，点B在边CD上，且 CD＝3DE. 将△ADE沿AE对折至△AFE，延长EF交边BC 于点G，连接AG，CF下列结论：①点G是BC的中点；②FG=FC；③ $∠$ GAE=45°；④GE=BG+DE.其中正确的是（）

A、①② B、①③④ C、②③ D、①②③④

查看试题解析

二、填空题

11. 如图，两个直角三角形重叠在一起，将其中一个沿点B到点C的方向平移到 $Δ D E F$ 的位置， $A B = 10$ ， $D H = 4$ ，平移距离为6，则阴影部分的面积为．

查看试题解析
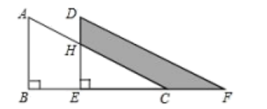12. 矩形ABCD中，AB＝5，BC＝4，点E是AB边上一点，AE＝3，连接DE，点F是BC延长线上一点，连接AF，且∠F＝ $\frac{1}{2}$ ∠EDC，则BF＝.

查看试题解析
13. 如图、已知AD、BC相交于点O， $A B ∥ C D ∥ E F$ ，如果 $C E = 2$ ， $E B = 6$ ， $F D = 1.5$ ，那么 $A D =$ ．

查看试题解析
14. 如图，四边形ABCD中， $A D ∥ B C ∥ E F$ ，如果 $A E = 3 ， A B = 8 ， C D = 10$ ，则 $C F$ 的长是．

查看试题解析
15. 如图，在△ABC中，点D是AB边上的一点，且AD＝3BD，连接C并取CD的中点E，连接BE，若∠ACD＝∠BED＝45°，且CD＝6 $\sqrt{2}$ ，则AB的长为．

查看试题解析

三、解答题

16. 如图，梯形 $A B C D$ 中， $A D ∥ B C$ ，点E是边 $A D$ 的中点，联结 $B E$ 并延长交 $C D$ 的延长线于点F，交 $A C$ 于点G．求证： $E F \cdot G B = B F \cdot G E$ ．

查看试题解析
17. 在四边形ABCD中， $D C ∥ A B$ ， $∠ D A B = 90 °$ ， $A C ⊥ B C$ ， $A C = B C$ ， $∠ A B C$ 的平分线分别交AD、AC于点E、F，求 $\frac{E F}{B F}$ 的值．

查看试题解析
18. 如图，在 $△ A B C$ 中，点 $E$ 在 $A B$ 上，过 $E$ 作 $E G ∥ B C$ 交 $A C$ 于点 $G$ ，连接 $C E$ ，过点 $G$ 作 $D G ∥ E C$ 交 $A B$ 于 $D$ ．求证： $A E^{2} = A B \cdot A D$ ．

查看试题解析
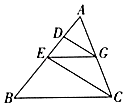19. 如图，在四边形ABCD中，E是对角线BD上的一点，EF//AB，EM//CD，求 $\frac{E F}{A B} + \frac{E M}{C D}$ 的值.

查看试题解析

四、综合题

20. 如图，已知 $A B ∥ C D$ ， $A C$ 与 $B D$ 相交于点E，点F在线段 $B C$ 上， $\frac{A B}{C D} = \frac{1}{2}$ ， $\frac{B F}{C F} = \frac{1}{2}$ ．

(1)、求证： $A B ∥ E F$ ；

(2)、求 $A B ： E F ： C D$ ．

查看试题解析
21. 探究：如图①，直线l₁∥l₂∥l₃ ，点C在l₂上，以点C为直角顶点作∠ACB＝90°，角的两边分别交l₁与l₃于点A、B，连结AB，过点C作CD⊥l₁于点D，延长DC交l₃于点E．

(1)、求证：△ACD∽△CBE．

(2)、应用：如图②，在图①的基础上，设AB与l₂的交点为F，若AC＝BC，l₁与l₂之间的距离为2，l₂与l₃之间的距离为1，则AF的长度是　　．

查看试题解析
22. 如图，点E是矩形ABCD的边BA延长线上一点，连接ED，EC，EC交AD于点G，作
CF∥ED交AB于点F，DC＝DE．

(1)、求证：四边形CDEF是菱形；

(2)、若BC＝3，CD＝5，求AE的长；

(3)、在（2）的条件下，求AG的长。

查看试题解析
23. 请阅读以下材料，并完成相应的问题：
角平分线分线段成比例定理，如图1，在△ABC中，AD平分∠BAC，则 $\frac{A B}{A C} = \frac{B D}{C D}$ ．
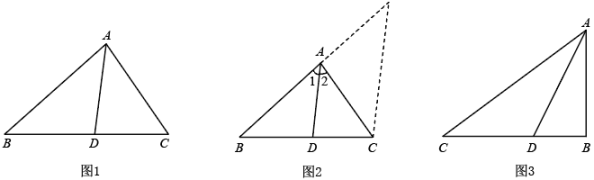
下面是这个定理的部分证明过程．
证明：如图2，过点C作 $C E ∥ D A$ ．交BA的延长线于点E．…
任务：

(1)、请按照上面的证明思路，写出该证明过程的剩余部分；

(2)、如图3，已知Rt△ABC中，AB＝3，BC＝4，∠ABC＝90°，AD平分∠BAC，求△ABD的周长．

查看试题解析