2023-2024学年北师大版数学七年级上册 5.6 应用一元一次方程——追赶小明 同步练习（提升卷）
试卷更新日期：2023-11-02 类型：同步测试
一、选择题
-
1. 小明步行每分钟行60米，小华骑自行车每分钟行160米，二人同时同地相背而行5分钟后，小华立即调头来追甲，再经过（ ）分钟小华可追上小明.A、 B、 C、10 D、112. 如图，小明想到A站乘公交车，发现他与公交车的距离为 ． 假设公交车的速度是小明速度的5倍．若要保证小明不会错过这辆公交车，则小明到A站之间的距离最大为（ ）
A、 B、 C、 D、3. 甲、乙两人从相距3600m的A，B两地相向而行，他们离B地的路程s(m)与从出发到相遇的运动时间t(单位：min)之间的函数关系如图．甲骑车、乙步行，甲的速度是乙的3倍，相遇后，乙坐甲的车原路返回．若甲骑车的速度一直不变，则乙返回所用时间是（ ）
A、5min B、15min C、20min D、30min4. 甲，乙两车从地驶向地，并以各自的速度匀速行驶，甲车比乙车早行驶 ， 并且甲车途中休息了 ， 如图是甲，乙两车行驶的路程与甲车行驶的时间的函数图象，则在乙车行驶的过程中两车相距时，乙车行驶的时间为（ ）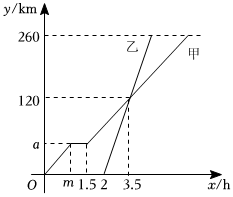
A、或 B、或 C、或 D、或5. 甲、乙两人从A地出发前往B地，其中甲先出发1 h.如图是甲、乙行驶路（单位：km），（单位：km）随甲行驶时间x（单位：h）变化的图象.当乙追上甲时，乙行驶的时间是（ ）
A、2 h B、3 h C、2.5 h D、3.5 h6. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术，其中方程术是其最高的代数成就．《九章算术》中有这样一个问题：“今有善行者行一百步，不善行者行六十步．今不善行者先行一百步，善行者追之，问几何步及之？”译文：“相同时间内，走路快的人走100步，走路慢的人只走60步．若走路慢的人先走100步，走路快的人要走多少步才能追上？(注：步为长度单位)”设走路快的人要走x步才能追上，根据题意可列出的方程（ ）60
A、x=100-x B、x=100+x C、x=100+x D、x=100-x7. 如图，A，B两地相距1200m，小车从A地出发，以8m/s的速度向B地行驶，中途在C地停靠3分钟.大货车从B地出发，以5m/s的速度向A地行驶，途经D地（在A地与C地之间）时沿原路返回B点取货两次，且往返两次速度都保持不变（取货时间不计），取完两批货后再出发至A点.已知： ， 则直至两车都各自到达终点时，两车相遇的次数为（ ）
A、2 B、3 C、4 D、58. 某市新能源出租车的收费标准如下：3千米以内（包括3千米）收费元，超过3千米后，每超1千米就加收元（不足1千米按1千米计费）．若某人乘出租车的费用为元，则他乘坐出租车行驶的距离不可能是（ ）A、6千米 B、千米 C、千米 D、7千米9. 如图，点A在数轴上表示的数是-8，点B在数轴上表示的数是16．若点A以6个单位长度/秒的速度向右匀速运动，同时点B以2个单位长度/秒的速度向左匀速运动．问：当AB＝8时，运动时间为多少秒？（ ）
A、2秒 B、13.4秒 C、2秒或4秒 D、2秒或6秒10. 一段跑道长100米，两端分别记为点A、B．甲、乙两人分别从A、B两端同时出发，在这段跑道上来回练习跑步，甲跑步的速度是6m/s，乙跑步的速度为4m/s，练习了足够长时间，他们经过了多次相遇，相遇点离A端不可能是（ ）A、60米 B、0米 C、20米 D、100米二、填空题
-
11. A、B两地之间相距120千米，其中一部分是上坡路，其余全是下坡路，小华骑电动车从A地到B地，再沿原路返回，去时用了5.5小时，返回时用了4.5小时，已知下坡路段小华的骑车速度是每小时30千米，那么上坡路段小华的骑车速度为.12. 斑马线前“车让人”，反映了城市的文明程度，但行人一般都会在红灯亮起前通过马路．某人行横道全长24米，小明以的速度过该人行横道，行至处时，9秒倒计时灯亮了．小明要在红灯亮起前通过马路，他的速度至少要提高到原来的倍．13. 元朝朱世杰的《算学启蒙》一书记载：“今有良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日迫及之.”意思是：现有良马每天行走240里，驽马每天行走150里，驽马先走12天，问良马几天可以追上驽马？两匹马行走路程S（里）与行走时间t（日）的函数关系如图所示，则图中交点P的坐标是 ．
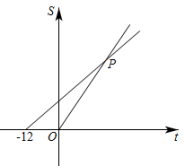14. 小明和小刚从学校出发去敬老院送水果，小明带着东西先走了 ， 小刚才出发.若小明每分钟行 ， 小刚每分钟行 ， 则小刚用分钟可以追上小明.三、综合题
-
15. 学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地．两人之间的距离y（米）与时间t（分钟）之间的函数关系如图所示．
(1)、点B的坐标是 ．(2)、根据图象信息，甲的速度为米/分钟，当t=分钟时甲乙两人相遇；(3)、求点A的坐标．16. 甲、乙两车分别从B，A两地同时出发，甲车匀速前往A地，乙车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；设甲、乙两车距A地的路程为y（千米），乙车行驶的时间为x（时），y与x之间的图象如图所示．
(1)、求乙车到达B地的时间；(2)、求乙车到达B地时甲车距A地的路程；(3)、求甲车行驶途中，甲、乙两车相距40千米时，乙车行驶的时间．17. 为了方便乘客出行，深圳宝安国际机场安装了图1所示的平地电梯，如图2是其示意图，已知电梯AB的长度为200米，小刚和小明两人不乘电梯在地面匀速行走时，小刚每分钟行走的路程是小明的1.2倍，且1.5分钟后，小刚比小明多行走15米．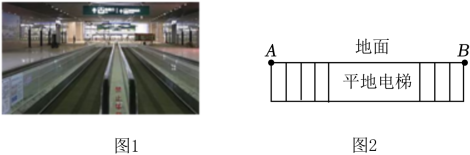
(1)、求两人在地面上每分钟各行走多少米？(2)、若两人同时从A点出发在平地电梯上行走，电梯向前行驶的同时两人仍保持原来在地面上匀速行走的速度在电梯上行走，当小刚到达B处时，小明还剩20米才到达B处．①求电梯每分钟行驶多少米？
②当小刚到达B处时，发现有一袋行李忘在了A处，于是马上以每分钟a米的速度从地面返回A处，拿了行李后立即乘平地电梯（同时按原来在地面上匀速行走的速度行走）去B处和小明汇合，要使小明到达B点后等待的时间不超过4分钟，求a的最小值．
18. 在一条高速公路上依次有A，B，C三地，甲车从A地出发匀速驶向C地，到达C地休息后调头（调头时间忽略不计）按原路原速驶向B地，甲车从A地出发后，乙车从C地出发匀速驶向A地，两车同时到达目的地．两车距A地路程与甲车行驶时间之间的函数关系如图所示．请结合图象信息，解答下列问题：
(1)、甲车行驶的速度是 ， 乙车行驶的速度是 ．(2)、求图中线段所表示的y与x之间的函数解析式，并直接写出自变量x的取值范围；(3)、乙车出发多少小时，两车距各自出发地路程的差是？请直接写出答案．19. 某校组织七年级师生到从化进行秋游活动，学校联系了快乐旅游公司提供车辆．该公司现有50座与35座两种车型．如果用35座的，会有5人没座位；如果全部换成50座，则可少用2辆车，而且多出15个座位．若35座客车日租金为每辆250元，50座客车日租金为每辆300元．(1)、该校七年级师生一共多少人参加了这次秋游活动？(2)、这次秋游活动一共有几种租车方案？哪一种方案最划算？(3)、从学校到目的地的路程为90千米，原计划3小时到达．在开了三分之一路程之后，堵车半小时．为了按时到达，请你帮司机算一下，车速应提高到每小时多少千米？20. 小明家、新华书店、学校在一条笔直的公路旁，某天小明骑车上学，当他骑了一段后，想起要买某本书，于是又返回到刚经过的新华书店，买到书后继续骑车去学校，他本次骑车上学的过程中离家距离与所用的时间的关系如图所示，请根据图象提供的信息回答下列问题：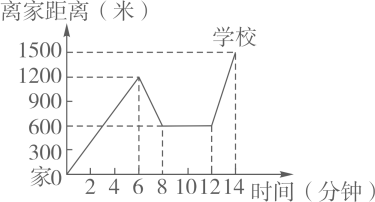
(1)、小明家到学校的距离是米；小明在书店停留了分钟；(2)、如果骑车的速度超过了300米/分就超越了安全限度，小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗？请说明理由；(3)、请直接写出小明出发后多长时间离家的距离为900米？