2023-2024学年北师大版数学七年级上册 5.5 应用一元一次方程——“希望工程”义演同步练习（提升卷）

试卷更新日期：2023-11-02 类型：同步测试

进入出卷网下载

一、选择题

1. 福州某机械厂加工车间有35名工人，平均每名工人每天加工大齿轮5个或小齿轮10个，已知2个大齿轮和3个小齿轮配成一套，问分别安排多少名工人加工大、小齿轮，才能刚好配套？若设加工大齿轮的工人有x名，则可列方程为（）

A、3×5x＝2×10（35-x） B、2×5x＝3×10（35-x） C、3×10x＝2×5（35-x） D、2×10x＝3×5（35-x）

查看试题解析
2. 在目前的疫情环境下，口罩成了人们生活中的必需品.现某口罩厂共有 $60$ 名工人，每名工人每天可以生产 $150$ 个罩面或 $600$ 个耳绳.已知一个罩面需要配两个耳绳，为使每天生产的罩面和耳绳刚好配套，设安排 $x$ 名员工生产罩面，则下列方程正确的是（）

A、 $150 x = 2 \times 600 (60 - x)$ B、 $2 \times 150 (60 - x) = 600 x$ C、 $150 (60 - x) = 2 \times 600 x$ D、 $2 \times 150 x = 600 (60 - x)$

查看试题解析
3. 学校需制作若干块标志牌，由一名工人做要50h完成.现计划由一部分工人先做4h，然后增加5人与他们一起做6h完成这项工作.假设这些工人的工作效率一样，具体应先安排多少人工作？小华的解法如下：设先安排x人做4h.所列方程为 $\frac{4 x}{50} + \frac{6 (x + 5)}{50} = 1$ ，其中“ $\frac{4 x}{50}$ ”表示的意思是“x人先做4h完成的工作量”，“ $\frac{6 (x + 5)}{50}$ ”表示的意思是“增加5人后 $(x + 5)$ 人再做6小时完成的工作量”.小军所列的方程如下： $\frac{(4 + 6) x}{50} + \frac{5 \times 6}{50} = 1$ ，其中，“ $\frac{(4 + 6) x}{50}$ ”表示的含义是（）

A、x人先做4h完成的工作量. B、先工作的x人前4h和后6h一共完成的工作量. C、增加5人后，新增加的5人完成的工作量. D、增加5人后， $(x + 5)$ 人再做6h完成的工作量.

查看试题解析
4. 20名学生在进行一次科学实践活动时，需要组装一种实验仪器，仪器是由三个 $A$ 部件和两个 $B$ 部件组成.在规定时间内，每人可以组装好10个 $A$ 部件或20个 $B$ 部件.那么，在规定时间内，最多可以组装出实验仪器的套数为（）

A、 50 B、60 C、100 D、150

查看试题解析
5. 某中学的学生自己动手整修操场，七年级的学生说：“如果让我们单独工作，7.5小时能完成”；八年级的学生说：“如果让我们单独工作，5小时能完成.”现两个年级学生一起工作1小时，剩下的部分再让七年级单独完成需x小时，可列方程（）

A、 $\frac{1}{7.5} - \frac{1}{5} - \frac{x}{7.5} = 1$ B、 $\frac{1}{7.5} - \frac{1}{5} + \frac{x}{7.5} = 1$ C、 $\frac{1}{7.5} + \frac{1}{5} - \frac{x}{7.5} = 1$ D、 $\frac{1}{7.5} + \frac{1}{5} + \frac{x}{7.5} = 1$

查看试题解析
6. 某项工程，甲单独完成需要45天，乙单独完成需要30天，若乙先单独做22天，剩下的由甲去完成，问：甲、乙一共用几天可完成全部工作？设甲、乙共用x天完成，则符合题意的方程是（）

A、 $\frac{x - 22}{45} + \frac{22}{30} = 1$ B、 $\frac{x + 22}{30} + \frac{x}{45} = 1$ C、 $\frac{x + 22}{45} + \frac{22}{30} = 1$ D、 $\frac{x}{30} + \frac{x - 22}{45} = 1$

查看试题解析
7. 鸡兔同笼问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”图是嘉淇解题过程，需要补足横线上符号所代表的内容，则下列判断错误的是（）

A、□代表（35﹣x） B、☆代表鸡的足数 C、〇代表2 D、△代表2

查看试题解析
8. 数学课堂上，老师出示了如下例题：
整理一批图书，由一个人做要40h完成．现计划由一部分人先做4h，然后增加2人与他们一起做8小时，完成这项工作．假设这些人的工作效率相同，具体应先安排多少人工作？设安排x人先做4h．小亮列的方程是： $\frac{4 x}{40} + \frac{8 (x + 2)}{40} = 1$ ，其中，“ $\frac{4 x}{40}$ ”表示的意思是“x人先做4h完成的工作量”，“ $\frac{8 (x + 2)}{40}$ ”表示的意思是“增加2人后，（x+2）人再做8小时完成的工作量”．小宇列的方程是： $\frac{(4+8) x}{40} + \frac{2 \times 8}{40} = 1$ ，其中，“ $\frac{(4 + 8) x}{40}$ ”表示的意思是（）

A、先工作的x人前4小时和后8小时一共完成的工作量 B、增加2人后，（x+2）人再做8小时完成的工作量 C、增加2人后，新增加的2人完成的工作量 D、x人先做4小时完成的工作量

查看试题解析
9. 某超市在“元旦”活动期间，推出如下购物优惠方案：
①一次性购物在100元（不含100元）以内，不享受优惠；②一次性购物在100元（含100元）以上，350元（不含350元）以内，一律享受九折优惠；③一次性购物在350元（含350元）以上，一律享受八折优惠；小敏在该超市两次购物分别付了85元和270元，如果小敏把这两次购物改为一次性购物，则小敏至少需付款（）元

A、284 B、308 C、312 D、320

查看试题解析
10. 甲、乙、丙三家超市为了促销一种定价为m元的商品，甲超市连续两次降价20%；乙超市一次性降价40%；丙超市第一次降价30%，第二次降价10%，此时顾客要购买这种商品，最划算的超市是（）

A、甲 B、乙 C、丙 D、三家都一样

查看试题解析

二、填空题

11. 小明和小红制作小红旗，100个小红旗两人合作20分钟完成，已知小明每分钟做2个，则小红每分钟做个．

查看试题解析
12. 一件工程甲单独做50天可完成，乙单独做75天可完成，现在两个人合作.但是中途乙因事离开几天，从开工后40天把这件工程做完.则乙中途离开了天.

查看试题解析
13. 某项工作甲单独做8天完成，乙单独做12天完成，若甲先做3天，然后甲、乙合作完成此项工作，则甲一共做了天，

查看试题解析
14. 某街道居委会需印制主题为“做文明有礼北京人，垃圾分类从我做起”的宣传单，其附近两家图文社印制此种宣传单的收费标准如图所示：

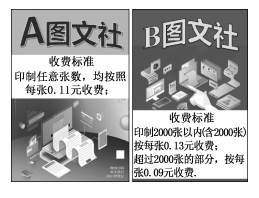(1)、为达到及时宣传的目的，街道居委会同时在A、B两家图文社共印制了1500张宣传单，印制费用共计179元，则街道居委会在A图文社印制了张宣传单；

(2)、为扩大宣传力度，街道居委会还需要再加印5000张宣传单，在A、B两家图文社中，选择图文社更省钱（填A或B）．

查看试题解析
15. 一项工程甲单独做需要10天完成，乙单独做需要8天完成．若甲先做1天，然后由甲、乙合作完成此项工程，则甲一共做了天．

查看试题解析

三、综合题

16. 某班计划买一些乒乓球和乒乓球拍，现了解情况如下：甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍，乒乓球拍每副定价100元，乒乓球每盒定价20元．经洽谈后，甲店每买一副球拍赠一盒乒乓球，乙店全部按定价的9折优惠，该班需球拍5副，乒乓球若干盒（不少于5盒）．

(1)、若该班需购买乒乓球x盒，用含x的式子分别表示在甲、乙两家商店购买的费用．

(2)、当分别购买20盒、30盒乒乓球时，去哪家商店购买更合算？

查看试题解析
17. 某厂用铁皮做罐头盒，每张铁皮可制盒身15个或盒底45个，1个盒身与2个盒底配成一套罐头盒.为了充分利用材料，要求制成的盒身和盒底恰好配套.现有151张铁皮，最多可做多个包装盒?
为了解决这个问题，小敏设计一种解决方案：把这些铁皮分成两部分，一部分做盒身，一部分做盒盖.

(1)、请探究小敏设计的方案是否可行?请说明理由.

(2)、若是你解决这个问题，怎样设计解决方案，使得材料充分利用?请说明理由.

查看试题解析
18. 在新冠肺炎防疫工作中，某药店出售酒精与口罩，酒精每瓶定价12元，口罩每个定价6元，药店现开展促销活动，向大家提供两种优惠方案：①买一瓶酒精送一个口罩；②酒精和口罩都按定价的80%付款.小明为班级采购30瓶酒精，x个口罩（ $x > 30$ ）.

(1)、求小明分别按方案①和方案②购买，需要付的款（用含x的代数式表示）；

(2)、购买多少个口罩时，方案①和方案②费用相同？

(3)、若两种优惠方案可同时使用，当 $x = 50$ 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方案.

查看试题解析
19. 2021年国庆期间，某景区对门票采用灵活的售票方法吸引游客，按团队人数分段定价售票，信息如表：
团队人数（人）
小于10人
10人及以上且小于30人
30人及以上
门票单价
60元
50元
40元
注：本题中的门票款不含导游的门票.

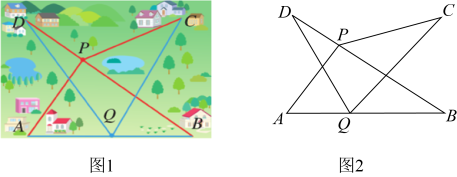
(1)、导游小张于10月1日带了一个30人的旅游团到该景区，请问需要支付多少元门票款？

(2)、导游小李于10月1日带A团，10月2日带B团都到该景区旅游，共付门票款1800元，A，B两个团队合计42人，A团人数比B团人数少，求A，B两个团队各有多少人？

查看试题解析
20. 问题提出：
如图1，A、B、C、D表示四个村庄，村民们准备合打一口水井.

(1)、问题解决：
若水井的位置现有P、Q两种选择方案.点P在线段 $B D$ 上，点Q在线段 $A B$ 上，哪一种方案的水井到各村庄的距离总和较小？请说明你判断的理由.

(2)、你能给出一种使水井到各村庄的距离之和最小的方案吗？若能，请图2中标出水井的位置点M，并说明理由.

(3)、问题拓展：
如果（2）问中找出的水井经过招标，由两个工程队修建（不存在同时修建）. 已知甲工程队单独完成需要80天，乙工程队单独完成需要120天，且甲工程队比乙工程队每天多修建 $0.5 m$ .
问水井要修建几米？

(4)、若甲工程队每天的施工费为0.5万元，乙工程队每天的费用是0.25万元，为了缩短工期和节约资金，则甲工程队最多施工几天才能使工程款不超过35万元？（甲、乙两队的施工时间不足一天按一天算）.

查看试题解析

团队人数（人）	小于10人	10人及以上且小于30人	30人及以上
门票单价	60元	50元	40元

2023-2024学年北师大版数学七年级上册 5.5 应用一元一次方程——“希望工程”义演 同步练习（提升卷）

一、选择题

二、填空题

三、综合题

2023-2024学年北师大版数学七年级上册 5.5 应用一元一次方程——“希望工程”义演同步练习（提升卷）