吉林省长春市榆树市2023-2024学年九年级上学期月考数学试卷(10月份)
试卷更新日期:2023-11-02 类型:月考试卷
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 计算 的结果是( )A、 B、 C、 D、2. 一元二次方程 的二次项系数、一次项系数和常数项分别为( )A、2,4,5 B、2, ,5 C、2,4, D、2, ,3. 用配方法解方程 , 变形后的结果正确的是( )A、 B、 C、 D、4. 下列各组图形不是相似图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,直线 , 直线、与这三条平行线分别交于点、、和点、、若 , , , 则的长为( )
5. 如图,直线 , 直线、与这三条平行线分别交于点、、和点、、若 , , , 则的长为( )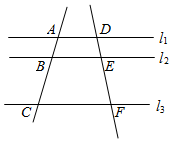 A、 B、 C、 D、6. 下列立体图形中,俯视图与主视图不同的是( )A、
A、 B、 C、 D、6. 下列立体图形中,俯视图与主视图不同的是( )A、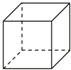 正方体
B、
正方体
B、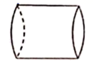 圆柱
C、
圆柱
C、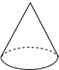 圆锥
D、
圆锥
D、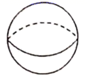 球
7. 某校初三年级举行班级篮球友谊赛,每两个班都要进行一场比赛,张老师告诉小丽总共要进行120场比赛,小丽想通过列方程求出参与比赛的班级数.设参与比赛的班级有 个,则所列方程正确的是( )A、 B、 C、 D、8. 如图,抛物线的顶点在的边所在的直线上运动,的顶点的坐标为 , 点的坐标为 , 若抛物线与的边、都有公共点,则的取值范围是( )
球
7. 某校初三年级举行班级篮球友谊赛,每两个班都要进行一场比赛,张老师告诉小丽总共要进行120场比赛,小丽想通过列方程求出参与比赛的班级数.设参与比赛的班级有 个,则所列方程正确的是( )A、 B、 C、 D、8. 如图,抛物线的顶点在的边所在的直线上运动,的顶点的坐标为 , 点的坐标为 , 若抛物线与的边、都有公共点,则的取值范围是( )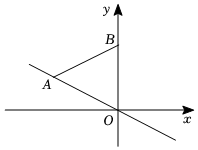 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
9. 若 , 则化简的结果为 .10. 若 , 则 .11. 一元二次方程根的判别式的值是 .12. 某数学兴趣小组学习“用频率估计概率”知识后,在对某品种蔬菜的发芽情况进行试验后,并将试验结果制成如下的表格:
试验次数
发芽次数
发芽频率
据此估计这批蔬菜种子发芽的概率是精确到 .
13. 最简二次根式与是同类二次根式,则a= , b= .14. 如图,在中, , 点、是边上的点,点在边上,连结、 , 将分别沿直线和折叠,使点、的对称点重合在边上的点处.若 , , 则的长是 .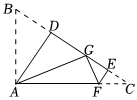
三、计算题(本大题共1小题,共6.0分)
-
15. 先化简 , 然后从 , , 中选取一个的合适的数作为的值代入求值.
四、解答题(本大题共11小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
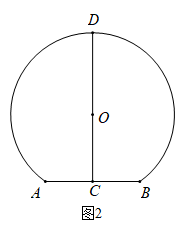
16. 解下列方程:(1)、 .(2)、 .17. 计算:(1)、;(2)、 .18. 如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端分米,C为中点,D为拱门最高点,圆心O在线段上,分米,求拱门所在圆的半径.

 19. 某社区组织 , , , 四个小区的居民进行核酸检测,有很多志愿者参与此项检测工作,志愿者王明和李丽分别被随机安排到这四个小区中的一个小区组织居民排队等候.(1)、王明被安排到小区进行服务的概率是 .(2)、请用列表法或画树状图法求出王明和李丽被安排到同一个小区工作的概率.20. 如图,图、图、图均为的正方形网格,线段的端点均在格点上,按要求在图、图、图中各画一条线段 , 将线段分为:两部分.
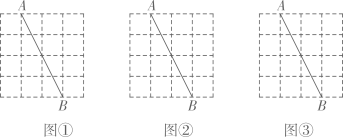
19. 某社区组织 , , , 四个小区的居民进行核酸检测,有很多志愿者参与此项检测工作,志愿者王明和李丽分别被随机安排到这四个小区中的一个小区组织居民排队等候.(1)、王明被安排到小区进行服务的概率是 .(2)、请用列表法或画树状图法求出王明和李丽被安排到同一个小区工作的概率.20. 如图,图、图、图均为的正方形网格,线段的端点均在格点上,按要求在图、图、图中各画一条线段 , 将线段分为:两部分.要求:(1)所画线段的位置不同.(2)点、均在格点上.
 21. 如图,在 中, , , .求 的三个三角函数值.
21. 如图,在 中, , , .求 的三个三角函数值.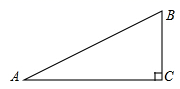 22. 如图,已知抛物线经过 , 两点.
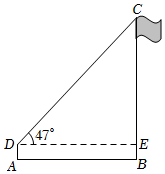
22. 如图,已知抛物线经过 , 两点.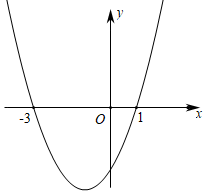 (1)、求抛物线的解析式和顶点坐标.(2)、当时,直接写出的取值范围.23. 年某县总量为亿元,计划到年全县总量实现亿元的目标.如果每年的年平均增长率相同,求该县这两年总量的年平均增长率是多少?24. 如图,为了测量旗杆的高度 , 在离旗杆底部米的处,用高米的测角仪测得旗杆顶端处的仰角为求旗杆的高.精确到米
(1)、求抛物线的解析式和顶点坐标.(2)、当时,直接写出的取值范围.23. 年某县总量为亿元,计划到年全县总量实现亿元的目标.如果每年的年平均增长率相同,求该县这两年总量的年平均增长率是多少?24. 如图,为了测量旗杆的高度 , 在离旗杆底部米的处,用高米的测角仪测得旗杆顶端处的仰角为求旗杆的高.精确到米参考数据: , ,
 25. 如图,已知二次函数的图象与轴交于、两点,与轴交于点 , 直线的函数表达式为 .
25. 如图,已知二次函数的图象与轴交于、两点,与轴交于点 , 直线的函数表达式为 .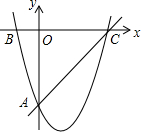 (1)、求二次函数的表达式及顶点坐标;(2)、求时的取值范围;(3)、点是线段上任意一点不含端点 , 过点作轴的平行线交二次函数图象交于点 , 若点的横坐标 , 求为何值时,线段有最大值,最大值是多少.26. 在函数的学习过程中,我们经历“画函数图象一利用函数图象研究其性质一运用函数图象解决问题”的学习过程.
(1)、求二次函数的表达式及顶点坐标;(2)、求时的取值范围;(3)、点是线段上任意一点不含端点 , 过点作轴的平行线交二次函数图象交于点 , 若点的横坐标 , 求为何值时,线段有最大值,最大值是多少.26. 在函数的学习过程中,我们经历“画函数图象一利用函数图象研究其性质一运用函数图象解决问题”的学习过程.下面根据学习函数的过程和方法,探究分段函数的相关性质和应用.
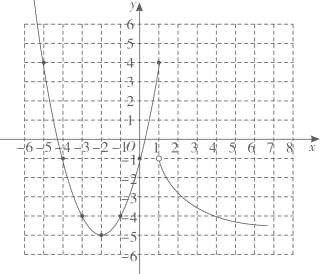 (1)、在如图所示的平面直角坐标系中,画出了分段函数图象的一部分,补全该分段函数的图象.
(1)、在如图所示的平面直角坐标系中,画出了分段函数图象的一部分,补全该分段函数的图象.写出该分段函数的一条性质:;
(2)、直线与该分段函数的图象有个交点,则的取值范围是;(3)、若该分段函数图象上有两点 , 且 , 则的取值范围是;(4)、当时,函数值的取值范围为 , 当取某个范围内的任意值时,为定值,直接写出满足条件的的取值范围及其对应的值.
-