吉林省松原市乾安县2023-2024学年九年级上学期期中数学试题

试卷更新日期：2023-11-02 类型：期中考试

进入出卷网下载

一、选择题（本大题共6小题，每小题2分，共12分）

1. 一元二次方程 $4 x^{2} - 6 x + 1 = 0$ 的二次项系数、一次项系数、常数项分别是（）

A、4，6，1 B、4，6， $- 1$ C、4， $- 6$ ， 1 D、4， $- 6$ ， $- 1$

查看试题解析
2. 中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量，下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若关于 $x$ 的一元二次方程 $x^{2} - 3 x + m = 0$ 有两个相等的实数根，则实数 $m$ 的值为（）

A、 $- 9$ B、 $- \frac{9}{4}$ C、 $\frac{9}{4}$ D、9

查看试题解析
4. 已知二次函数 $y = - 3 {(x - 2)}^{2} - 3$ ，下列说法正确的是（）

A、对称轴为 $x = - 2$ B、顶点坐标为 $(2 ， 3)$ C、函数的最大值是 $- 3$ D、函数的最小值是 $- 3$

查看试题解析
5. 如图，在 $△ A B C$ 中， $∠ C = 90^{°} ， ∠ B A C = 70^{°}$ ，将 $△ A B C$ 绕点 A 顺时针旋转 $70^{°} ， B$ 、C 旋转后的对应点分别是 $B^{'}$ 和 $C^{'}$ ，连接 $B B^{'}$ ，则 $∠ B B^{'} C^{'}$ 的度数是（）

A、 $35^{°}$ B、 $40^{°}$ C、 $45^{°}$ D、 $50^{°}$

查看试题解析
6. 如图，抛物线 $y = a x^{2} + c$ 经过正方形 $O A B C$ 的三个顶点A，B，C，点B在 $y$ 轴上，则 $a c$ 的值为（）

A、 $- 1$ B、 $- 2$ C、 $- 3$ D、 $- 4$

查看试题解析

二、填空题（本大题共8小题，每小题3分，共24分）

7. 已知关于x的方程 $x^{2} + m x - 20 = 0$ 的一个根是 $- 4$ ，则它的另一个根是．

查看试题解析
8. 已知一元二次方程 $x^{2} - 3 x + 1 = 0$ 有两个实数根 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} - x_{1} x_{2}$ 的值等于．

查看试题解析
9. 将抛物线 $y = {(x + 3)}^{2}$ 向下平移1个单位长度，再向右平移个单位长度后，得到的新抛物线经过原点．

查看试题解析
10. 如图，一名学生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是 $y = - \frac{1}{12} (x - 10) (x + 4)$ ，则铅球推出的距离 $O A =$ m．

查看试题解析
11. 在方格纸上建立如图所示的平面直角坐标系，将 $△ A B O$ 绕点O按顺时针方向旋转 $90 °$ ，得 $△ A^{'} B^{'} O$ ，则点A的对应点 $A^{'}$ 的坐标为．

查看试题解析
12. 我们古代数学家研究过一元二次方程．下面是我国南宋数学家杨辉在1275年提出的一个问题：“直田积（矩形面积）八百六十四步（平方步），只云阔（宽）不及长一十二步（宽比长少一十二步），问阔及长各几步．”意思是一块田是矩形，矩形面积为 $864 m^{2}$ ，长比宽多 $12 m$ ，如果设宽为 $x m$ ，则列出的方程为．

查看试题解析
13. 如图，将面积为7的正方形 $O A B C$ 和面积为9的正方形 $O D E F$ 分别绕原点O顺时针旋转，使 $O A$ ， $O D$ 落在数轴上，点A，D在数轴上对应的数字分别为a，b，则 $b - a =$ ．

查看试题解析
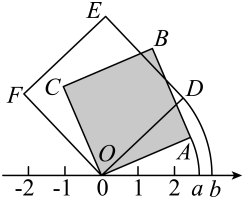14. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图像的一部分与x轴的一个交点坐标为 $(3 ， 0)$ ，对称轴为直线 $x = 1$ ，结合图像给出下列结论：
① $a b c > 0$ ；
② $b = 2 a$ ；
③ $3 a + c = 0$ ；
④关于x的一元二次方程 $a x^{2} + b x + c + k^{2} = 0 (a \neq 0)$ 有两个不相等的实数根；
⑤若点 $(m ， y_{1})$ ， $(- m + 2 ， y_{2})$ 均在该二次函数图象上，则 $y_{1} = y_{2}$ ．其中正确结论的序号为．

查看试题解析

三、解答题（每小题5分，共20分）

15. 解方程： $x^{2} - 3 x + 2 = 0$ .

查看试题解析
16. 在平面直角坐标系xOy中，抛物线 $y = - x^{2} + b x + c$ 经过点 $(2 ， 3)$ ，对称轴为直线 $x = 1$ ，求抛物线的表达式．

查看试题解析
17. 如图所示，在 $△ A B C$ 中， $∠ B = 40 °$ ，将 $△ A B C$ 绕点A逆时针旋转至 $△ A D E$ 处，使点B落在BC延长线上的D点处，求 $∠ B D E$ 的度数．

查看试题解析
18. 为增强学生身体素质，某校开展篮球比赛，赛制为单循环形式（每两队之间赛一场）．现计划安排21场比赛，应安排多少个球队参赛．

查看试题解析

四、解答题（每小题7分，共28分）

19. 如图，在建立平面直角坐标系的网格纸中，每个小方格都是边长为1个单位长度的小正方形， $△ A B C$ 的顶点均在格点上，点P的坐标为 $(- 1 ， 0)$ ．
⑴把 $△ A B C$ 绕点P旋转 $180 °$ 得到 $△ A^{'} B^{'} C^{'}$ ，作出 $△ A^{'} B^{'} C^{'}$ ；
⑵把 $△ A B C$ 向右平移7个单位长度得到 $△ A^{″} B^{″} C^{″}$ ，作出 $△ A^{″} B^{″} C^{″}$ ；
⑶ $△ A^{'} B^{'} C^{'}$ 与 $△ A^{″} B^{″} C^{″}$ 是否成中心对称？若是，则找出对称中心 $P^{'}$ ，并写出其坐标；若不是，请说明理由．

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} - (2 m + 1) x + m^{2} + m = 0$ ．

(1)、求证：无论m取何值时，方程都有两个不相等的实数根；

(2)、设该方程的两个实数根为a，b，若 $(2 a + b) (a + 2 b) = 20$ ，求m的值．

查看试题解析
21. 如图，点 $O$ 是等边三角形 $A B C$ 内的一点， $∠ B O C = 150 °$ ，将 $△ B O C$ 绕点 $C$ 按顺时针旋转得到 $△ A D C$ ，连接 $O D$ ， $O A$ 。

(1)、求 $∠ O D C$ 的度数；

(2)、若 $O B = 4$ ， $O C = 5$ ，求 $A O$ 的长。

查看试题解析
22. 超市的某种牛奶平均每天可销售20箱，每箱盈利30元．为了尽快减少库存，商场决定采取适当的降价措施．经调查发现，若每箱降价1元，每天可多售5箱，若设每箱降价x元．

(1)、根据题意，填表：

每箱利润（元）
销售量（箱）
利润（元）
降价前
30
20
600
降价后
①
②

(2)、若每天盈利1200元，则每箱应降价多少元？

查看试题解析

五、解答题（每小题8分，共16分）

23. 在杭州举行的亚运会比赛中，一名运动员在 $10 m$ 高的跳台进行跳水，身体（看成一点）在空中的运动轨迹是一条抛物线，运动员离水面OB的高度 $y (m)$ 与离起跳点A的水平距离 $x (m)$ 之间的函数关系如图所示，运动员离起跳点A的水平距离为 $1 m$ 时达到最高点，当运动员离起跳点A的水平距离为 $3 m$ 时离水面的距离为 $7 m$ ．

(1)、求y关于x的函数表达式；

(2)、求运动员从起跳点到入水点的水平距离OB的长．

查看试题解析
24. 阅读材料：解方程 ${(x^{2} - 1)}^{2} - 5 (x^{2} - 1) + 4 = 0$ ，我们可以将 $(x^{2} - 1)$ 视为一个整体，然后设 $(x^{2} - 1) = y$ ，则 ${(x^{2} - 1)}^{2} = y^{2}$ ，原方程化为 $y^{2} - 5 y + 4 = 0$ ，解得 $y_{1} = 1$ ， $y_{2} = 4$ ．
当 $y = 1$ 时， $x^{2} - 1 = 1$ ， $∴ x^{2} = 2$ ， $∴ x = \pm \sqrt{2}$
当 $y = 4$ 时， $x^{2} - 1 = 4$ ， $∴ x^{2} = 5$ ， $∴ x = \pm \sqrt{5}$
$∴$ 原方程的解为 $x_{1} = \sqrt{2}$ ， $x_{2} = - \sqrt{2}$ ， $x_{3} = \sqrt{5}$ ， $x_{4} = - \sqrt{5}$
根据上面的解答，解决下面的问题：

(1)、填空：在由原方程得到方程①的过程中，利用法达到降次的目的，体现了的数学思想；

(2)、解方程 $x^{4} - x^{2} - 12 = 0$ ．

查看试题解析

六、解答题（每小题10分，共20分）

25. 我们可以通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整．
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上， $∠ E A F = 45 °$ ，连接EF ，则 $E F = B E + D F$ ，试说明理由．

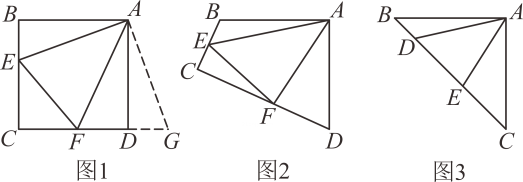(1)、思路梳理
$∵ A B = A D$ ，
$∴$ 把 $△ A B E$ 绕点A逆时针旋转 $90 °$ 至 $△ A D G$ ，可使AB与AD重合．
$∵ ∠ A D C = ∠ B = 90 °$ ，
$∴ ∠ F D G =$ ，点F、D、G共线．
根据，易证 $△ A F E ≌$ ，得 $E F = B E + D F$ ．

(2)、类比引申
如图2，四边形ABCD中， $A B = A D$ ， $∠ B A D = 90 °$ ，点E、F分别在边BC、CD上， $∠ E A F = 45 °$ ，若 $∠ B$ 、 $∠ D$ 都不是直角，则当 $∠ B$ 与 $∠ D$ 满足等量关系时，仍有 $E F = B E + D F$ ．

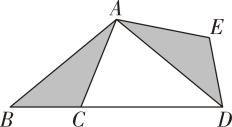
(3)、联想拓展
如图3，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点D、E均在边BC上，且 $∠ D A E = 45 °$ ．猜想BD、DE、EC应满足的等量关系，并写出推理过程．

查看试题解析

26. 根据以下素材，探索完成任务．

如何设计拱桥景观灯的悬挂方案？
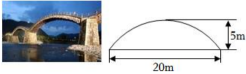
素材1	图1中有一座拱桥，图2是其抛物线形桥拱的示意图，某时测得水面宽 $20 m$ ，拱顶离水面 $5 m$ ．据调查，该河段水位在此基础上再涨 $1.8 m$ 达到最高．		图1 图2
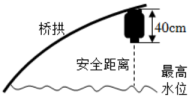
素材2	为迎佳节，拟在图1桥洞前面的桥拱上悬挂 $40 c m$ 长的灯笼，如图3．为了安全，灯笼底部距离水面不小于 $1 m$ ；为了实效，相邻两盏灯笼悬挂点的水平间距均为 $1.6 m$ ；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．		图3
问题解决
任务1	确定桥拱形状	在图2中建立合适的直角坐标系，求抛物线的函数表达式．
任务2	探究悬挂范围	在你所建立的坐标系中，仅在安全的条件下，确定悬挂点的纵坐标的最小值和横坐标的取值范围．
任务3	拟定设计方案（填空即可）	给出一种符合所有悬挂条件的灯笼数量，并根据你所建立的坐标系，求出最左边一盏灯笼悬挂点的横坐标．

查看试题解析

	每箱利润（元）	销售量（箱）	利润（元）
降价前	30	20	600
降价后	①	②