吉林省长春市朝阳区2023-2024学年七年级上学期期中数学试题
试卷更新日期:2023-11-02 类型:期中考试
一、选择题(每小题3分,共24分)
-
1. 的相反数是( )A、 B、2 C、 D、2. 2023年06月,国家基础地理信息中心航空航天遥感数据获取公开招标,该项目的预算金额约为24800000元,24800000这个数用科学记数法表示为( )A、 B、 C、 D、3. “神舟十六号”载人飞船上有一种零件的尺寸标准是(单位:mm),则下列零件尺寸不合格的是( )A、295mm B、298mm C、304mm D、310mm4. 下列关于单项式的说法中,正确的是( )A、系数是 , 次数是3 B、系数是 , 次数是3 C、系数是 , 次数是2 D、系数是 , 次数是35. 下列代数式中,表示“与的2倍的差”的是( )A、 B、 C、 D、6. 若 , 则的值是( )A、5 B、 C、 D、97. 北京时间2023年10月9日某时刻以下四个地点的气温情况如图所示.例如,长春的实时气温是零上6℃,当日的最高气温是零上19℃、最低气温是零上5℃,该日的气温日较差(气温日较差=日最高气温-日最低气温)是14℃.则这四个地点该日的气温日较差最大的是( )
长春
6℃
19/5℃
漠河
℃
14/℃
北京
13℃
24/10℃
南极
℃
℃
A、长春 B、漠河 C、北京 D、南极8. 有理数、在数轴上所对应的点如图所示,则下列结论正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共18分)
-
9. 如果定义水位上升0.3米记作米,那么水位下降0.5米记作米.10. 比较大小:(填“>”、“<”或“=”).11. 将多项式按的降幂排列为: .12. 用四舍五入法将17.0946精确到百分位的结果是 .13. 某产业去年年产值为亿元,今年比去年增长了15%.那么该企业今年的年产值将达到亿元.14. 细菌是靠分裂进行生殖的,也就是1个细菌分裂成2个细菌,分裂完的细菌长大以后又能进行分裂.例如,图中所示为某种细菌分裂的电镜照片,显示这种细菌每20分钟就能分裂一次.1个这种细菌经过3个小时可以分裂成个细菌.
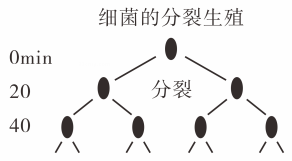
三、解答题(本大题共9小题,共78分)
-
15. 直接写出计算结果:(1)、(2)、(3)、(4)、(5)、(6)、16. 计算:(1)、 .(2)、 .17. 计算: .18. 把下列各数在数轴上表示出来,并按从小到大的顺序排列,用“<”连接起来:
3, , 1.5, , 0.
 19. 学习有理数计算后,冬冬同学過到这样一道题目: .
19. 学习有理数计算后,冬冬同学過到这样一道题目: .冬冬的解法如下:
第一步
第二步
第三步
第四步
冬冬的计算过程从第 ▲ 步开始出现错误,错误的原因是 ▲ . 请你把这道题正确的计算过程写下来.
20. 若、互为相反数,、互为倒数, , 是最大的负整数,求的值.21. 小明把一张长方形纸板的四周各剪去一个同样大小的小正方形,如图所示,长方形纸板的长为 , 宽为 , 小正方形的边长为 .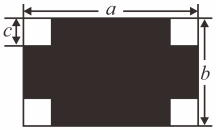 (1)、用含、、的代数式表示剩余纸板(阴影部分)的面积.(2)、当 , , 时,求剩余纸板的面积.22. 出租车司机小李某天上午营运都是在东西走向的道路上进行的,如果规定向东为正,向西为负,他这天上午行车里程(单位:千米)如下: , , , , , .(1)、将最后一位乘客送到目的地时,小李距出发地多远?此时在出发地东边还是西边?(2)、若汽车耗油量为每千米升,这天上午小李开出租车共耗油多少升?(3)、若该城市出租车起步价为10元,起步里程为3千米(包括3千米),超过部分每千米2.2元.求这天上午小李开出租车共收入多少元?23. 如图①,在数轴上,点为坐标原点,点、、、表示的数分别是-8、3、9、13.动点、同时出发,动点从点出发,沿数轴以每秒2个单位的速度向点运动,当点运动到点后,立即按原来的速度返回.动点从点出发,沿数轴以每秒1个単位的速度向终点运动.当点到达点时,点也停止运动,设点的运动时间为秒.
(1)、用含、、的代数式表示剩余纸板(阴影部分)的面积.(2)、当 , , 时,求剩余纸板的面积.22. 出租车司机小李某天上午营运都是在东西走向的道路上进行的,如果规定向东为正,向西为负,他这天上午行车里程(单位:千米)如下: , , , , , .(1)、将最后一位乘客送到目的地时,小李距出发地多远?此时在出发地东边还是西边?(2)、若汽车耗油量为每千米升,这天上午小李开出租车共耗油多少升?(3)、若该城市出租车起步价为10元,起步里程为3千米(包括3千米),超过部分每千米2.2元.求这天上午小李开出租车共收入多少元?23. 如图①,在数轴上,点为坐标原点,点、、、表示的数分别是-8、3、9、13.动点、同时出发,动点从点出发,沿数轴以每秒2个单位的速度向点运动,当点运动到点后,立即按原来的速度返回.动点从点出发,沿数轴以每秒1个単位的速度向终点运动.当点到达点时,点也停止运动,设点的运动时间为秒.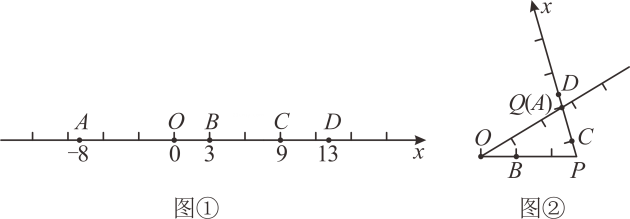 (1)、点与原点的距离是 .(2)、点从点向点运动过程中,点与原点的距离是(用含的代数式表示).(3)、点从点向点运动过程中,当点与原点的距离恰好等于点与点的距离时,求的值.(4)、在点、的整个运动过程中,若将数轴在点和点处各折一下,使点与点重合,如图②所示,当所构成的三角形中恰好有两条边相等时,直接写出的值.
(1)、点与原点的距离是 .(2)、点从点向点运动过程中,点与原点的距离是(用含的代数式表示).(3)、点从点向点运动过程中,当点与原点的距离恰好等于点与点的距离时,求的值.(4)、在点、的整个运动过程中,若将数轴在点和点处各折一下,使点与点重合,如图②所示,当所构成的三角形中恰好有两条边相等时,直接写出的值.