宁夏吴忠市同心县重点中学2023-2024学年九年级上学期数学月考考试试卷(9月)
试卷更新日期:2023-11-01 类型:月考试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、3. 关于x的方程 实数根的情况,下列判断正确的是( )A、有两个相等实数根 B、有两个不相等实数根 C、没有实数根 D、有一个实数根4. 已知抛物线 , 下列结论错误的是( )A、抛物线开口向上 B、抛物线的对称轴为直线 C、抛物线的顶点坐标为 D、当时,y随x的增大而增大5. 有一个人患了流行性感冒,经过两轮传染后共有144人患了流行性感冒,则每轮传染中平均一个人传染的人数是( )A、14 B、11 C、10 D、96. 把抛物线向左平移个单位,再向下平移个单位,所得抛物线的顶点坐标是( )A、 B、 C、 D、7. 若 , , 三点都在二次函数的图象上,则 , , 的大小关系为( )A、 B、 C、 D、8. 一次函数与二次函数在同一平面直角坐标系中的图象可能是( )A、
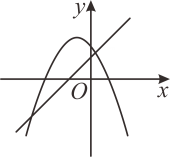 B、
B、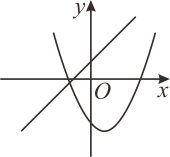 C、
C、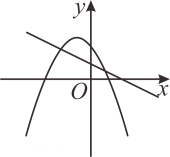 D、
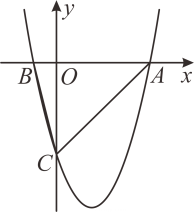
D、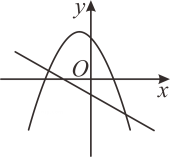 9. 抛物线关于轴对称的抛物线的解析式是( )A、 B、 C、 D、10. 在平面直角坐标系中,已知二次函数的图象如图所示,有下列个结论:
9. 抛物线关于轴对称的抛物线的解析式是( )A、 B、 C、 D、10. 在平面直角坐标系中,已知二次函数的图象如图所示,有下列个结论: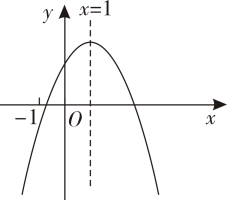
;;;; .
其中正确的结论有( )A、个
B、个
C、个
D、个二、填空题(本大题共10小题,共30.0分)
-
11. 一元二次方程x2=2x的根是 .12. 一元二次方程 的二次项系数是 , 常数项是 .13. 若函数的图象与轴没有公共点,则的取值范围是 .14. 现要在一个长为 , 宽为的矩形花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为 , 设小道的宽度应是 , 列方程得: .
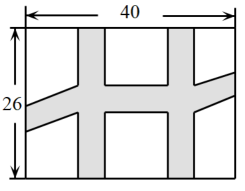 15. 设 分别为一元二次方程 的两个实数根,则 .16. 将方程化为一般式,其结果是 .17. 已知点是抛物线上的两点,则这条抛物线的对称轴为直线 .18. 某县推行“”课后服务以后,教师的工作时间持续增加,已知第一周平均工作时长为小时,到第三周时,平均工作时长为小时,设这两周工作时长的平均增长率为 , 则可列方程为 .19. 若将二次函数化成(m,p为常数)的形式,则的值为 .20. 代数式的最小值为 .
15. 设 分别为一元二次方程 的两个实数根,则 .16. 将方程化为一般式,其结果是 .17. 已知点是抛物线上的两点,则这条抛物线的对称轴为直线 .18. 某县推行“”课后服务以后,教师的工作时间持续增加,已知第一周平均工作时长为小时,到第三周时,平均工作时长为小时,设这两周工作时长的平均增长率为 , 则可列方程为 .19. 若将二次函数化成(m,p为常数)的形式,则的值为 .20. 代数式的最小值为 .三、解答题
-
21. 列方程(组)解应用题
端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?
22. 解下列方程:(1)、 ;(2)、 .23. 若关于的一元二次方程一个根为 , 求方程另一个根和的值.24. 抛物线与轴交于点 . (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、求它与轴的交点和抛物线顶点的坐标.25. 用一段长为的篱笆围成一个靠墙的矩形菜园,墙的长度为 .
设垂直于墙的一边长为xm,则平行于墙的一边长为用含的代数式表示;