北京市重点大学附中2023-2024学年九年级上学期数学开学考试试卷
试卷更新日期:2023-11-01 类型:开学考试
一、选择题(本大题共8小题,共16.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 在中, , 是边上的高, , 则等于( )
 A、 B、 C、 D、3. 下列命题中错误的是( )A、矩形的对角线相等 B、对角线相等的四边形是矩形
A、 B、 C、 D、3. 下列命题中错误的是( )A、矩形的对角线相等 B、对角线相等的四边形是矩形
C、两组对边分别相等的四边形是平行四边形 D、平行四边形的对边相等4. 下列曲线中不能表示是的函数的是( )A、 B、
B、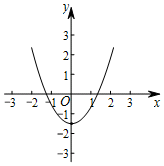 C、
C、 D、
D、 5. 若一次函数的函数值随的增大而减小,且图象与轴的负半轴相交,那么对和的符号判断正确的是( )A、 , B、 , C、 , D、 ,6. 若关于的一元二次方程有一个根为 , 则的值为( )A、 B、 C、 D、7. 某校足球队队员年龄分布如图所示,下面关于该队年龄统计数据的说法正确的是( )
5. 若一次函数的函数值随的增大而减小,且图象与轴的负半轴相交,那么对和的符号判断正确的是( )A、 , B、 , C、 , D、 ,6. 若关于的一元二次方程有一个根为 , 则的值为( )A、 B、 C、 D、7. 某校足球队队员年龄分布如图所示,下面关于该队年龄统计数据的说法正确的是( )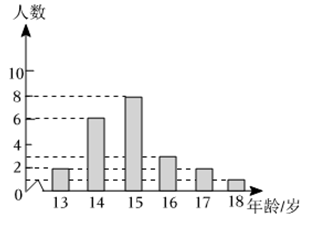 A、平均数比大 B、中位数比众数小
A、平均数比大 B、中位数比众数小
C、若今年和去年的球队成员完全一样,则今年方差比去年大
D、若年龄最大的选手离队,则方差将变小8. 如图,匀速地向该容器内注水(单位时间内注水体积相同),在注满水的过程中,满足容器中水面的高度y与时间x之间函数关系的图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(本大题共8小题,共16.0分)
-
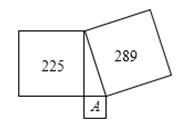
9. 若 在实数范围内有意义,则实数x的取值范围是.10. 如图,两个较大正方形的面积分别为225,289,中间所夹三角形为直角三角形,则字母A所代表的正方形的面积为 .
 11. 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 .
11. 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 . 12. 如图,矩形的顶点的坐标为 , 则 .
12. 如图,矩形的顶点的坐标为 , 则 . 13. 如图,在中,是的垂直平分线,若的周长为 , 则的周长为 .
13. 如图,在中,是的垂直平分线,若的周长为 , 则的周长为 . 14. 已知直线和直线平行,且过点 , 则此直线与轴的交点坐标为 .15. 如图,在平面直角坐标系中,四边形为正方形,点的坐标为若直线:和直线:被正方形的边所截得的线段长度相等,写出一组满足条件的与的值 .
14. 已知直线和直线平行,且过点 , 则此直线与轴的交点坐标为 .15. 如图,在平面直角坐标系中,四边形为正方形,点的坐标为若直线:和直线:被正方形的边所截得的线段长度相等,写出一组满足条件的与的值 . 16. 某快递员负责为 , , , , 五个小区取送快递,每送一个快递收益元,每取一个快递收益元,某天个小区需要取送快递数量如表
16. 某快递员负责为 , , , , 五个小区取送快递,每送一个快递收益元,每取一个快递收益元,某天个小区需要取送快递数量如表小区
需送快递数量
需取快递数量
(1)、如果快递员一个上午最多前往个小区,且要求他最少送快递件,最少取快递件,写出一种满足条件的方案 写出小区编号;(2)、在的条件下,如果快递员想要在上午达到最大收益,写出他的最优方案 写出小区编号 .三、解答题(本大题共8小题,共68.0分。解答应写出文字说明,证明过程或演算步骤)
-
17.(1)、计算;
(2)、解方程 .18. 已知:如图,、分别是▱的边、上的点,且 .
求证: . 19. 已知关于的一元二次方程有两个不相等的实数根.(1)、求的取值范围;
19. 已知关于的一元二次方程有两个不相等的实数根.(1)、求的取值范围;
(2)、若为正整数,且该方程的根都是整数,求的值.20. 已知一次函数的图象经过 , .(1)、求一次函数解析式;
(2)、若正比例函数与线段有公共点,直接写出的取值范围.21. 如图,已知Rt△ABC中,∠C=90°,AD是角平分线,CD=15,BD=25,求AC的长。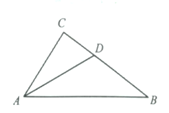 22. 为了解我国年第一季度个地区第一季度快递业务收入的情况,收集了这个地区第一季度快递业务收入单位:亿元的数据,并对数据进行了整理、描述和分析,给出如下信息.
22. 为了解我国年第一季度个地区第一季度快递业务收入的情况,收集了这个地区第一季度快递业务收入单位:亿元的数据,并对数据进行了整理、描述和分析,给出如下信息.
排在前位的地区第一季度快递业务收入的数据分别为: , , , ,
其余个地区第一季度快递业务收入的数据的频数分布表如下:快递业务收入
频数
第一季度快递业务收入的数据在这一组的是: , , , , , , , , ,
排在前位的地区、其余个地区、全部个地区第一季度快递业务收入的数据的平均数、中位数如下:前位的地区
其余个地区
全部个地区
平均数
中位数
根据以上信息,回答下列问题:
(1)、表中的值为 ▲ ;(2)、在下面的个数中,与表中的值最接近的是 ▲ 填写序号;
(3)、根据中的数据,预计这个地区年全年快递业务收入约为 ▲ 亿元.23. 对于正数 , 用符号表示的整数部分,例如 , , 点在第一象限内,以为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直其中垂直于轴的边长为 , 垂直于轴的边长为 , 那么,把这个矩形覆盖的区域叫做点的矩形域例如:点的矩形域是一个以为对角线交点,长为 , 宽为的矩形所覆盖的区域,如图所示,它的面积是 .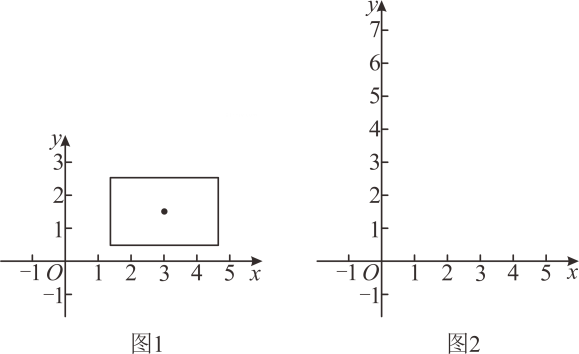
根据上面的定义,回答下列问题:
(1)、在图所示的坐标系中画出点的矩形域,该矩形域的面积是 ;(2)、点 , 的矩形域重叠部分面积为 , 则的值为 .24. 如图,是等腰直角三角形, , 为延长线上一点,连接 , 将线段绕点逆时针旋转得到线段 , 过点作于点 , 连接 . (1)、依题意补全图形;(2)、比较与的大小,并证明;(3)、连接 , 为的中点,连接 , 用等式表示线段之间的数量关系,并证明.
(1)、依题意补全图形;(2)、比较与的大小,并证明;(3)、连接 , 为的中点,连接 , 用等式表示线段之间的数量关系,并证明.