贵州省遵义市2023-2024学年八年级上学期数学月考考试试卷(10月)
试卷更新日期:2023-11-01 类型:月考试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 已知≌ , , , 则的度数为( )A、 B、 C、 D、2. 用三角板作 的边BC上的高,下列三角板的摆放位置正确的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图是某校门口的电动伸缩门,电动伸缩门利用了性质( )
3. 如图是某校门口的电动伸缩门,电动伸缩门利用了性质( ) A、四边形的不稳定性
A、四边形的不稳定性
B、三角形的稳定性
C、四边形的稳定性
D、三角形的不稳定性4. 如图,已知 , 则证明≌的理由是( ) A、 B、 C、 D、5. 一个多边形的每个外角都是 , 则这个多边形的边数为( )A、4 B、5 C、6 D、86. 如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( ) .
A、 B、 C、 D、5. 一个多边形的每个外角都是 , 则这个多边形的边数为( )A、4 B、5 C、6 D、86. 如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( ) .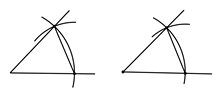 A、SAS B、ASA C、AAS D、SSS7. 四根木棒的长度分别为 , , , , 现从中取三根,使它们首尾顺次相接组成一个三角形,则这样的取法共有( )A、1种 B、2种 C、3种 D、4种8. 如图,直线 , 的直角顶点落在直线上,点落在直线上,若 , , 则的大小为( )
A、SAS B、ASA C、AAS D、SSS7. 四根木棒的长度分别为 , , , , 现从中取三根,使它们首尾顺次相接组成一个三角形,则这样的取法共有( )A、1种 B、2种 C、3种 D、4种8. 如图,直线 , 的直角顶点落在直线上,点落在直线上,若 , , 则的大小为( ) A、 B、 C、 D、9. 如图,有一块三角形玻璃,小明不小心将它打破. 带上这块玻璃,能配成同样大小的一块,其理由是( )
A、 B、 C、 D、9. 如图,有一块三角形玻璃,小明不小心将它打破. 带上这块玻璃,能配成同样大小的一块,其理由是( )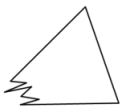 A、 B、 C、 D、10. 根据图中给定的条件,下列各图中可以判断与一定相等的是( )
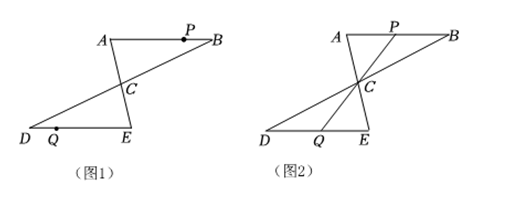
A、 B、 C、 D、10. 根据图中给定的条件,下列各图中可以判断与一定相等的是( )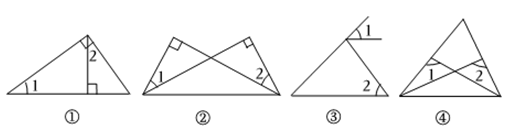 A、 B、 C、 D、11. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的处接住她后用力一推,爸爸在处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和.爸爸在处接住小丽时,小丽距离地面的高度是( )
A、 B、 C、 D、11. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的处接住她后用力一推,爸爸在处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和.爸爸在处接住小丽时,小丽距离地面的高度是( )
 A、1m B、1.6m C、 D、12. 如图, , , 分别平分 , , , 于点 , , 的面积为 , 则的周长为( )
A、1m B、1.6m C、 D、12. 如图, , , 分别平分 , , , 于点 , , 的面积为 , 则的周长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共16.0分)
-
13. 已知≌ , 且的周长为 , 若 , , .14. 如图,在四边形中, , 若沿图中虚线剪去 , 则 .
 15. 如图,在中,与是的两条高, , , 则 .
15. 如图,在中,与是的两条高, , , 则 .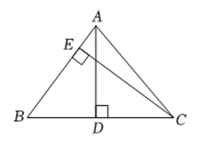 16. 如图,点为定角的平分线上的一个定点,且与互补,若在绕点旋转的过程中,其两边分别与、相交于、两点,则以下结论:①恒成立;②的值不变;③四边形的面积不变;④的长不变,其中正确的序号为 .
16. 如图,点为定角的平分线上的一个定点,且与互补,若在绕点旋转的过程中,其两边分别与、相交于、两点,则以下结论:①恒成立;②的值不变;③四边形的面积不变;④的长不变,其中正确的序号为 .
三、解答题(本大题共9小题,共98.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 如图,直线经过点 , , , .
 (1)、分别求、及的度数;
(1)、分别求、及的度数;
(2)、通过这道题,你能说明为什么三角形的内角和是吗?18. 如图是雨伞在开合过程中某时刻的截面图,伞骨 , , 分别是 , 的中点, , 是连接弹簧和伞骨的支架,且 , 在弹簧向上滑动的过程中,试说明平分 . 19. 一个多边形如果内角都相等,并且满足其一个内角的度数是其相对应外角度数的整数倍,就称这个多边形为“整数多边形”,已知一个“整数多边形”一个内角的度数是其相对应外角度数的倍,求这个“整数多边形”的边数及其内角和.20. 如图,点、、、在直线上、之间不能直接测量 , 点、在异侧,测得 , , .
19. 一个多边形如果内角都相等,并且满足其一个内角的度数是其相对应外角度数的整数倍,就称这个多边形为“整数多边形”,已知一个“整数多边形”一个内角的度数是其相对应外角度数的倍,求这个“整数多边形”的边数及其内角和.20. 如图,点、、、在直线上、之间不能直接测量 , 点、在异侧,测得 , , . (1)、求证:≌;
(1)、求证:≌;
(2)、若 , , 求的长度.21. 为了解学生对所学知识的应用能力,某校老师在八年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端 , 的距离无法直接测量,请同学们设计方案测量 , 的距离.甲、乙两位同学分别设计出了如下两种方案:
甲:如图 , 先在平地上取一个可以直接到达点 , 的点 , 连接并延长到点 , 连接并延长到点 , 使 , , 连接 , 测出的长即可;
乙:如图 , 先确定直线 , 过点作直线 , 在直线上找可以直接到达点的一点 , 连接 , 作 , 交直线于点 , 最后测量的长即可.
甲、乙两个同学的方案是否可行?请说明理由.22. 如图, , , 于 . (1)、求证:平分;
(1)、求证:平分;
(2)、若 , , 求的长.23. 在一个各内角都相等的多边形中,每一个内角都比相邻外角的倍还大 ,(1)、求这个多边形的边数;
(2)、若将这个多边形剪去一个角,剩下多边形的内角和是多少?