四川省成都市双流区重点学校2023-2024学年八年级上学期数学月考考试试卷（10月）

试卷更新日期：2023-11-01 类型：月考试卷

进入出卷网下载

一、选择题（本大题共8小题，共24分）

1. 在实数：3.14159， $\sqrt[3]{64}$ ，1.010010001…，π， $\frac{22}{7}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 以下不能构成直角三角形的是（）

A、 $a = 1$ ， $c = \sqrt{3}$ ， $b = 2$ B、 $∠ A + ∠ C = ∠ B$ C、 $a$ ： $b$ ： $c = 2$ . ： $3$ ： $4$ D、 $∠ A$ ： $∠ B$ ： $∠ C = 1$ ： $3$ ： $2$

查看试题解析
3. 当 $a$ 满足时，二次根式 $\sqrt{a + 3}$ 有意义．（）

A、 $a \geq 3$ B、 $a > 3$ C、 $a \geq - 3$ D、 $a > - 3$

查看试题解析
4. 在平面直角坐标系 $x O y$ 中，点 $M (- 4 ， 2)$ 关于x轴对称的点的坐标是（）

A、 $(- 4 ， 2)$ B、 $(4 ， 2)$ C、 $(- 4 ， - 2)$ D、 $(4 ， - 2)$

查看试题解析
5. 下列命题是假命题的是（）

A、三角形具有稳定性 B、周长相等的两个三角形全等
C、全等三角形的对应边相等 D、等腰三角形的两个底角相等

查看试题解析
6. 菲尔兹奖是数学领域的一项国际大奖，常被视为数学界的诺贝尔奖，每四年颁发一次，最近一届获奖者获奖时的年龄（单位：岁）分别为：30，40，34，36，则这组数据的中位数是（）

A、34 B、35 C、36 D、40

查看试题解析
7. 关于一次函数 $y = - 2 x + 3$ ，下列结论正确的是（）

A、图象过点 $(1 ， - 1)$ B、图象与 $x$ 轴的交点是 $(0 ， 3)$ C、 $y$ 随 $x$ 的增大而增大 D、函数图象不经过第三象限

查看试题解析
8. 一次函数 $y = k x + b$ 与 $y = k b x$ ，它们在同一坐标系内的图象可能为（）

A、 B、 C、 D、

查看试题解析

二、非选择题（共96分）

9. $\sqrt{81}$ 的算术平方根是

查看试题解析
10. 已知 $\sqrt{a + 2} + | b - 4 | = 0$ ，则ab的立方根为．

查看试题解析
11. 小明妈妈给了小明 $100$ 元去买作业本，已知作业本的单价是 $1.5$ 元，小明购买了 $x$ 本作业本，剩余费用为 $y$ 元，则 $y$ 与 $x$ 的函数关系式为．

查看试题解析
12. 如图，数字代表所在正方形的面积，则A所代表的正方形的面积为．

查看试题解析
13. 如图，直线 $y = 2 x + 4$ 与 $x$ 轴、 $y$ 轴交于点 $A$ 、 $B$ ， $M$ 、 $N$ 分别是 $A B$ 、 $O A$ 的中点，点 $P$ 是 $y$ 轴上一个动点，当 $P M + P N$ 的值最小时，点 $P$ 的坐标为．

查看试题解析
14. 计算：

(1)、 $\sqrt{(- 3)^{2} + (- 2)^{2}} - \sqrt{\frac{1}{\sqrt{16}}} + (π - 2)^{0}$ ；

(2)、 $\sqrt{12} - \sqrt{6} \div \sqrt{2} - (1 - \sqrt{3})^{2}$

查看试题解析
15. 解方程：

(1)、 $(x - 1)^{2} - 9 = 0$ ；

(2)、 $2 (2 x - 1)^{3} + 16 = 0$

查看试题解析

16.

4

月

23

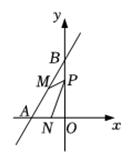日是“世界读书日”，向阳中学对在校学生课外阅读情况进行了随机问卷调查，共发放

100

份调查问卷，并全部收回

.

根据调查问卷，将课外阅读情况整理后，制成表格如表：

月阅读册数 $($ 本 $)$	$1$	$2$	$3$	$4$	$5$
被调查的学生数 $($ 人 $)$	$20$	$50$	$15$	$10$	$5$

请你根据以上信息，解答下列问题：

(1)、被调查的学生月平均阅读册数为本；

(2)、被调查的学生月阅读册数的中位数是；

(3)、在平均数、中位数这两个统计量中，更能反映被调查学生月阅读的一般水平；

(4)、若向阳中学共有学生

2000

人，用样本平均数估计四月份该校学生共阅读课外书籍多少本？

查看试题解析

17. 解答

(1)、已知 $2 a - 1$ 的平方根是 $\pm 3$ ， $3 a + b - 9$ 的立方根是 $2$ ， $c$ 是 $\sqrt{17}$ 的整数部分，求 $a + 2 b + c$ 的算术平方根．

(2)、已知实数 $a$ ， $b$ ， $c$ 在数轴上的对应点如图所示，化简 $\sqrt{a^{2}} - | c - a | + \sqrt{(b - c)^{2}}$ ．

查看试题解析
18. 在一条东西走向的河流一侧有一村庄 $C$ ，河边原有两个取水点 $A$ ， $B$ ，其中 $A B = A C$ ，由于某种原因，由 $C$ 到 $A$ 的路现在已经不通，该村为方便村民取水，决定在河边新建一个取水点 $D (A$ 、 $D$ 、 $B$ 在同一条直线上 $)$ ，并新修一条路 $C D$ ，测得 $C B = 6.5$ 千米， $C D = 6$ 千米， $B D = 2.5$ 千米．

(1)、求证： $C D ⊥ A B$ ；

(2)、求原来的路线 $A C$ 的长；

查看试题解析
19. 如图，已知四边形 $A B C D$ 是正方形， $E$ 是正方形内一点，以 $B C$ 为斜边作直角三角形 $B C E$ ，又以 $B E$ 为直角边作等腰直角三角形 $E B F$ ，且 $∠ E B F = 90 °$ ，连接 $A F$ ．

(1)、求证： $A F = C E$ ；

(2)、求证： $A F / / E B$ ；

(3)、若 $A B = 5 \sqrt{3}$ ， $\frac{B F}{C E} = \frac{\sqrt{6}}{3}$ ，求点 $E$ 到 $B C$ 的距离．

查看试题解析
20. 如图，数轴上点 $A$ 表示的数是 $- 1$ ， $0$ 是原点．以 $A O$ 为边作正方形 $A O B C$ ，以点 $A$ 为圆心线段 $A B$ 长为半径画半圆交数轴于 $P_{1}$ 、 $P_{2}$ 两点则点 $P_{1}$ 表示的数是．

查看试题解析
21. 如图，一个圆桶，底面直径为 $16 c m$ ，高为 $18 c m$ ，则一只小虫从下底部点 $A$ 爬到上底点 $B$ 处，问小虫所爬的最短路径长是 $(π$ 取 $3)$ ．

查看试题解析
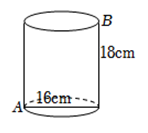22. 如图，在直线上依次摆着 $7$ 个正方形，已知倾斜放置的 $3$ 个正方形的面积分别为 $1$ ， $2$ ， $3$ ，水平放置的 $4$ 个正方形的面积是 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ， $S_{4}$ ，则 $S_{1} + 2 S_{2} + 2 S_{3} + S_{4} =$ ．

查看试题解析
23. 满足 $a^{2} + b^{2} = c^{2}$ 的三个正整数，称为勾股数 $.$ 若正整数 $a$ ， $n$ 满足 $a^{2} + n^{2} = (n + 1)^{2}$ ，这样的三个整数 $a$ ， $n$ ， $n + 1 ($ 如： $3$ ， $4$ ， $5$ 或 $5$ ， $12$ ， $13)$ 我们称它们为一组“完美勾股数”，当 $n < 115$ 时，共有组这样的“完美勾股数”．

查看试题解析
24. 如图，在矩形 $A B C D$ 中， $A B = 4$ ， $A D = 2$ ， $M$ 是 $A D$ 边的中点， $N$ 是 $A B$ 边上的一动点，将 $△ A M N$ 沿 $M N$ 所在直线翻折得到 $△ A' M N$ ，连接 $A' C .$ 在 $M N$ 上存在一动点 $P .$ 连接 $A' P$ 、 $C P$ ，则 $△ A' P C$ 周长的最小值是．

查看试题解析
25. 已知： $x = \frac{1}{\sqrt{5} - 2}$ ， $y = \frac{1}{\sqrt{5} + 2}$ ．

(1)、化简求值：求 $x^{2} - 3 x y + y^{2}$ 的值；

(2)、若 $x$ 的整数部分是 $m$ ， $y$ 的小数部分是 $n$ ，求 $m - n x$ 的值．

查看试题解析
26. 定义：如图①，点M、N把线段AB分割成AM、MN和BN，若以AM、MN、BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．

(1)、已知点M、N是线段AB的勾股分割点，若AM=2，MN=3，求BN的长；

(2)、如图②，在等腰直角△ABC中，AC=BC，∠ACB=90°，点M、N为边AB上两点，满足∠MCN=45°，求证：点M、N是线段AB的勾股分割点；
阳阳同学在解决第（2）小题时遇到了困难，陈老师对阳阳说：要证明勾股分割点，则需设法构造直角三角形，你可以把△CBN绕点C逆时针旋转90°试一试．

请根据陈老师的提示完成第（2）小题的证明过程；

(3)、在（2）的问题中，若∠ACM=15°，AM=1，CM= $\sqrt{3} + 1$ ，求BM的长．（提示：在直角三角形中， $30 °$ 角所对的直角边等于斜边的一半．）

查看试题解析
27. 在长方形 $A B C D$ 中，点 $E$ 是 $A D$ 中点，将 $△ A B E$ 沿 $B E$ 折叠后得到对应的 $△ G B E$ ，将 $B G$ 延长交直线 $D C$ 于点 $F$ ．

(1)、如果点 $G$ 在长方形 $A B C D$ 的内部，如图 $①$ 所示．
①求证： $G F = D F$ ；
②若 $D F = \frac{2}{3} C D$ ， $A D = 4$ ，求 $A B$ 的长度．

(2)、如果点 $G$ 在长方形 $A B C D$ 的外部，如图 $②$ 所示， $A D = k A B (k > 2)$ ，请用含 $k$ 的代数式表示 $\frac{D F}{C D}$ 的值．

查看试题解析