云南省昆明市重点学校2023-2024学年九年级上学期数学月考考试试卷(9月)
试卷更新日期:2023-11-01 类型:月考试卷
一、选择题(本大题共13小题,共38.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手,开展安全教育,下列安全图标是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. “篮球运动员投篮一次,投中篮筐”这一事件是( )A、确定事件 B、必然事件 C、不可能事件 D、不确定事件3. 一元二次方程根的情况是( )A、有两个不等的实数根 B、有两个相等的实数根
2. “篮球运动员投篮一次,投中篮筐”这一事件是( )A、确定事件 B、必然事件 C、不可能事件 D、不确定事件3. 一元二次方程根的情况是( )A、有两个不等的实数根 B、有两个相等的实数根
C、没有实数根 D、只有一个实数根4. 如图,将绕着点按顺时针方向旋转 , 点落在位置,点落在位置,若 , 则的度数是( )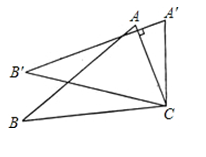 A、
A、
B、
C、
D、5. 将抛物线 向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为( )A、 B、 C、 D、6. 如图,是的弦,半径 , 为圆周上一点,若所对应圆心角的度数为 , 则的度数为( )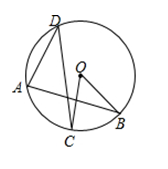 A、 B、 C、 D、7. 小强同学从 , , , , , 这六个数中任选一个数,满足不等式 的概率是( )A、 B、 C、 D、8. ⊙O的半径为2,则它的内接正六边形的边长为( )A、2 B、2 C、 D、29. 学校为了对学生进行劳动教育,开辟一个面积为平方米的矩形种植园,打算一面利用长为米的仓库墙面,其它三面利用长为米的围栏.如图,如果设矩形与墙面垂直的一边长为米,则下列方程中符合题意的是( )
A、 B、 C、 D、7. 小强同学从 , , , , , 这六个数中任选一个数,满足不等式 的概率是( )A、 B、 C、 D、8. ⊙O的半径为2,则它的内接正六边形的边长为( )A、2 B、2 C、 D、29. 学校为了对学生进行劳动教育,开辟一个面积为平方米的矩形种植园,打算一面利用长为米的仓库墙面,其它三面利用长为米的围栏.如图,如果设矩形与墙面垂直的一边长为米,则下列方程中符合题意的是( ) A、 B、 C、 D、10. 如图,PA、PB切⊙O于点A、B,PA=10,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是( )
A、 B、 C、 D、10. 如图,PA、PB切⊙O于点A、B,PA=10,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是( )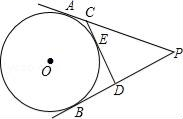 A、10 B、18 C、20 D、2211. 如图,二次函数的图象与轴交于、两点,与轴交于点 , 点的横坐标为 . 下面的四个结论中正确的是( )
A、10 B、18 C、20 D、2211. 如图,二次函数的图象与轴交于、两点,与轴交于点 , 点的横坐标为 . 下面的四个结论中正确的是( ) A、 B、 C、 D、12. 在等腰直角三角形中, , D是边上一动点,连接 , 以为直径的圆交于点E , 则长的最小值是( )
A、 B、 C、 D、12. 在等腰直角三角形中, , D是边上一动点,连接 , 以为直径的圆交于点E , 则长的最小值是( )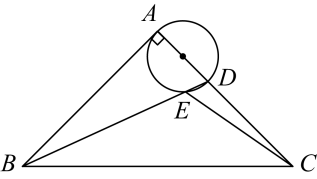 A、2 B、 C、 D、313. 抛物线可由抛物线平移得到,则平移的方式是( )A、向右平移个单位长度,再向上平移个单位长度 B、向左平移个单位长度,再向上平移个单位长度 C、向右平移个单位长度,再向下平移个单位长度 D、向左平移个单位长度,再向下平移个单位长度
A、2 B、 C、 D、313. 抛物线可由抛物线平移得到,则平移的方式是( )A、向右平移个单位长度,再向上平移个单位长度 B、向左平移个单位长度,再向上平移个单位长度 C、向右平移个单位长度,再向下平移个单位长度 D、向左平移个单位长度,再向下平移个单位长度二、填空题(本大题共3小题,共6.0分)
-
14. 若点的坐标是 , 则点关于原点的对称点坐标是 .15. 关于的方程的一个根是 , 则 .16. 圆锥的底面圆半径是1,侧面展开图的圆心角是90°,那么圆锥的母线长是 .
三、解答题(本大题共8小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 解方程:(1)、(2)、18. 如图,在平面直角坐标系中,的三个顶点坐标分别为 , , .
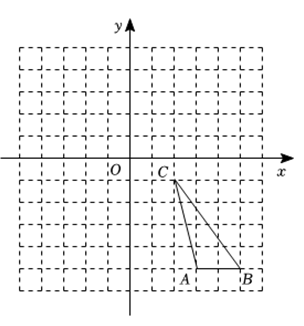
⑴画出关于轴对称的;
⑵画出绕点顺时针旋转后的;⑶在的条件下,求线段扫过的面积结果保留 .
19. 如图,是由转盘和箭头组成的两个装置,装置A , B的转盘分别被分成四、三个面积相等的扇形,装置A上的数字分别是1,2,3,4,装置B上的数字分别是3,4,5,这两个装置除了表面数字不同外,其它构造完全相同.现在分别同时用力转动A , B两个转盘.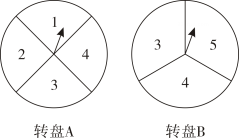 (1)、A转盘指向偶数的概率是 .(2)、请用列表法或画树状图的方法,求A、B转盘指向的数字之和不小于6的概率.20. 如图,将绕直角顶点顺时针旋转 , 得到 , 连接 , .
(1)、A转盘指向偶数的概率是 .(2)、请用列表法或画树状图的方法,求A、B转盘指向的数字之和不小于6的概率.20. 如图,将绕直角顶点顺时针旋转 , 得到 , 连接 , .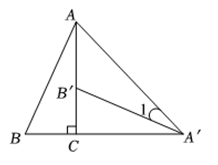 (1)、求的长;
(1)、求的长;
(2)、若 , 求的度数.21. 已知:如图,在中,直径的长为 , 弦的长为 , 的平分线交于点 , 求和的长.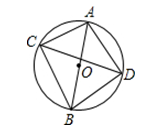 22. 普洱茶是中国名茶,某茶叶公司经销某品牌普洱茶,每千克成本为元,规定每千克售价需超过成本,但不高于元,经调查发现:其日销售量(千克)与售价(元/千克)之间的函数关系如图所示;
22. 普洱茶是中国名茶,某茶叶公司经销某品牌普洱茶,每千克成本为元,规定每千克售价需超过成本,但不高于元,经调查发现:其日销售量(千克)与售价(元/千克)之间的函数关系如图所示;
 (1)、求与之间的函数表达式;(2)、设日利润为元,求与之间的函数表达式,并说明日利润随售价的变化而变化的情况以及最大日利润.
(1)、求与之间的函数表达式;(2)、设日利润为元,求与之间的函数表达式,并说明日利润随售价的变化而变化的情况以及最大日利润.
