山东省济南市五中2023-2024学年九年级上学期月考数学试卷（10月）

试卷更新日期：2023-11-01 类型：月考试卷

进入出卷网下载

一、选择题（每小题4分共40分）

1. 下列方程是一元二次方程（　　）

A、x+2y=1 B、2x（x﹣1）=2x²+3 C、3x+ $\frac{1}{x}$ =4 D、x²﹣2=0

查看试题解析
2. 关于x的一元二次方程kx²+4x-2＝0有实数根，则k的取值范围是（　　）

A、k≥-2 B、k＞-2且k≠0 C、k≥-2且k≠0 D、k≤-2

查看试题解析
3. 把方程x²﹣8x+3＝0化成（x+m）²＝n的形式，则m，n的值是（）

A、4，13 B、﹣4，19 C、﹣4，13 D、4，19

查看试题解析
4. 如果 $\frac{c}{a + b} = \frac{a}{b + c} = \frac{b}{c + a} = k$ ，那么k的值为（　　）

A、-1 B、 $\frac{1}{2}$ C、2或-1 D、 $\frac{1}{2}$ 或-1

查看试题解析
5. 用配方法解一元二次方程2x²-3x-1＝0，配方正确的是（　　）

A、 ${(x - \frac{3}{2})}^{2} = \frac{13}{4}$ B、 ${(x - \frac{3}{4})}^{2} = \frac{1}{2}$ C、 ${(x - \frac{3}{4})}^{2} = \frac{17}{16}$ D、 ${(x - \frac{3}{2})}^{2} = \frac{11}{4}$

查看试题解析
6. 如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（）

A、 B、 C、 D、

查看试题解析
7. 在x²□2xy□y²的空格□中，分别填上“+”或“-”，在所得的代数式中，能构成完全平方式的概率是（　　）

A、1 B、 $\frac{3}{4}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
8. 已知如图（1）、（2）中各有两个三角形，其边长和角的度数如图上标注，则对图（1）、（2）中的两个三角形，下列说法正确的是（）

A、都相似 B、都不相似 C、只有（1）相似 D、只有（2）相似

查看试题解析
9.
如图，在▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（　　）

A、3：2 B、3：1 C、1：1 D、1：2

查看试题解析
10. 使用墙的一边，再用13m的铁丝网围成三边，围成一个面积为20m²的长方形，求这个长方形的两边长．设墙的对边长为xm ，可得方程（　　）

A、x（13-x）＝20 B、x• $\frac{13 - x}{2}$ ＝20 C、x（13- $\frac{1}{2}$ x）＝20 D、x• $\frac{13 - 2 x}{2}$ ＝20

查看试题解析

二、填空题（每小题4分共24分）

11. 若关于x的一元二次方程2x²-3x+c＝0的一个根是1，则c的值是．

查看试题解析
12. 关于x的方程（m-1）x²+2x-1＝0有两个不相等的实数根，则m的取值范围是．

查看试题解析
13. 在一个不透明的布袋中，有红球、黑球、白球共60个，它们除颜色外其他都相同．小明从中任意摸出一个球，查看色后放回并摇匀，通过多次摸球试验后，发现摸到红球、黑球的频率分别稳定在0.15和0.45，则他估计布袋中白球的个数约是个．

查看试题解析
14. 如图，点D、E分别在AB、AC上，且∠ABC＝∠AED．若DE＝4，AE＝5，BC＝8，则AB的长为

查看试题解析
15. 如图，点D在△ABC的边AC上，若要使△ABD与△ACB相似，可添加的一个条件是（只需写出一个）．

查看试题解析
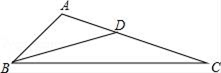16. 如图，已知点C、D是线段AB的两个黄金分割点，若线段AB的长10厘米，则线段CD长厘米．

查看试题解析

三、解答题：

17. 解下列方程：

(1)、x²＝25；

(2)、x²-4x+2＝0；

(3)、x²+3x+2＝0；

(4)、（x-1）（x+3）＝5（x-1）．

查看试题解析
18. 已知关于x的一元二次方程x²-2x+m-1＝0有两个实数根．

(1)、求m的取值范围；

(2)、设p是方程的一个实数根，且满足（p²-2p+3）（m+4）＝7，求m的值．

查看试题解析
19. 我校为了进行学雷锋爱心义卖活动，决定在操场划分一块面积为 $480$ 平方米的矩形场地 $.$ 若矩形场地的一边靠墙 $($ 墙长 $31$ 米 $)$ ，另外三边由总长为 $60$ 米的围绳围成，并且在垂直于墙的边上各设置了一个开口宽为 $1$ 米的入口和出口 $($ 如图 $) .$ 请根据方案计算出矩形场地的边长各是多少米？

查看试题解析
20. 在一个口袋中有3个完全相同的小球，把它们分别标号为1，2，3，随机地摸出一个小球记下标号后放回，再随机地摸出一个小球记下标号，求两次摸出小球的标号之和等于4的概率．

查看试题解析
21. 百货大楼服装柜在销售中发现：“宝乐”牌童装平均每天可售出20件，每件盈利40元．为了迎接“十•一”国庆节，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多售出2件．要想平均每天销售这种童装盈利1200元，那么每件童装应降价多少元？

查看试题解析
22.
如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．

(1)、求证：△ABM∽△EFA；

(2)、若AB=12，BM=5，求DE的长．

查看试题解析
23. 如图，点B、D、E在一条直线上，BE与AC相交于点F ， $\frac{A B}{A D}$ ＝ $\frac{B C}{D E}$ ＝ $\frac{A C}{A E}$ ．

(1)、求证：∠BAD＝∠CAE；

(2)、若∠BAD＝21°，求∠EBC的度数：

(3)、若连接EC ，求证：△ABD∽△ACE ．

查看试题解析
24. $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 5 cm$ ， $B C = 6 cm$ ，点P从点A开始沿边 $A B$ 向终点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边 $B C$ 向终点C以2cm/s的速度移动.如果点P、Q分别从点A、B同时出发，当点Q运动到点C时，两点停止运动.设运动时间为t秒.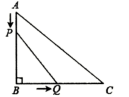

(1)、填空： $B Q =$ ， $P B =$ （用含t的代数式表示）；

(2)、是否存在t的值，使得 $△ P B Q$ 的面积等于 $4 {cm}^{2}$ ？若存在，请求出此时t的值；若不存在，请说明理由.

查看试题解析