吉林省长春市重点学校2023-2024学年八年级上学期第一次月考数学考试试卷
试卷更新日期:2023-11-01 类型:月考试卷
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 的立方根是( )A、 B、 C、 D、2. 计算的结果是( )A、 B、 C、 D、3. 下列运算中正确的是( )A、 B、 C、 D、4. 计算的结果是( )A、 B、 C、 D、5. 一个三角形的面积是 , 它的一边长是 , 那么这条边上的高为( )A、 B、 C、 D、6. 已知 , 则代数式的值是( )A、 B、 C、 D、7. 如图,在 中, ,根据尺规作图的痕迹,判断以下结论错误的是( )
 A、 B、 C、 D、8. 若 , 则的值为( )A、12 B、6 C、3 D、0
A、 B、 C、 D、8. 若 , 则的值为( )A、12 B、6 C、3 D、0二、填空题(本大题共6小题,共18.0分)
-
9. 因式分解: .10. 已知 , 则的值为 .11. 若 , 则的值为 .12. 等腰三角形的一个底角为 ,则它的顶角的度数为 .
13. 如图,是的角平分线,于点 , , , , 则长是 . 14. 如果是完全平方式,则 .
14. 如果是完全平方式,则 .三、解答题(本大题共10小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 计算:
(1)、;
(2)、;
(3)、;
(4)、 .16. 化简:
(1)、;
(2)、;
(3)、;
(4)、 .17. 因式分解:
(1)、;
(2)、;
(3)、;(4)、 .18. 先化简,再求值: , 其中 , .19. 已知:如图,点E,F在BC上,BE=CF,AB=DC.∠B=∠C.求证:AF=DE. 20. 某同学在计算一个多项式乘以时,因抄错运算符号,算成了加上 , 得到的结果是 , 请求出正确的结果.21. 如图,是由小方格组成的网格纸,每个方格的边长都是个单位长度,每个小正方形的顶点叫做格点,点、、、均在格点上.
20. 某同学在计算一个多项式乘以时,因抄错运算符号,算成了加上 , 得到的结果是 , 请求出正确的结果.21. 如图,是由小方格组成的网格纸,每个方格的边长都是个单位长度,每个小正方形的顶点叫做格点,点、、、均在格点上. (1)、在图中,作出向右平移个单位长度的三角形;
(1)、在图中,作出向右平移个单位长度的三角形;
(2)、在图中,作出绕点沿顺时针方向旋转得到的三角形;
(3)、在图中,请在线段上找到一点 , 连结和 , 使的值最小请保留作图痕迹 .22. 已知 , , 求下列各式的值:(1)、;(2)、 .23. 如图所示,长方形中, , 点从点出发,沿边向做往返运动,每秒移动 , 动直线与边重合,交于点 , 于点直线与点同时出发,沿方向移动,每秒移动 , 移动秒 , 当直线与边重合时,移动全部停止.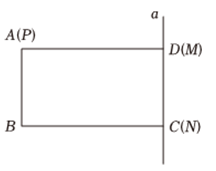 (1)、用含的代数式表示的长度;
(1)、用含的代数式表示的长度;
(2)、当为何值时,点在直线上;
(3)、连结 , , 直接写出当为何值时,与全等.24. 【感知】已知 , , 求的值.
解: , , 即 .
, ,
【探究】参考上述过程,解答下列问题: (1)、若 , , 则 ;(2)、如图所示,若 , , 求的值;(3)、若满足 , 求的值;(4)、如图 , 在长方形中, , , , 是 , 上的点,且 , 分别以 , 为边在长方形外侧作正方形和 , 若长方形的面积为 , 直接写出图中阴影部分的面积和为 .
(1)、若 , , 则 ;(2)、如图所示,若 , , 求的值;(3)、若满足 , 求的值;(4)、如图 , 在长方形中, , , , 是 , 上的点,且 , 分别以 , 为边在长方形外侧作正方形和 , 若长方形的面积为 , 直接写出图中阴影部分的面积和为 .