四川省绵阳市涪城区2023-2024学年八年级上学期数学月考考试试卷(10月)
试卷更新日期:2023-11-01 类型:月考试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
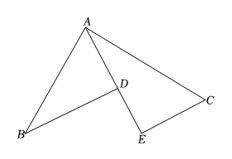
1. 下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是( )A、1,2,3 B、1,2,4 C、2,3,4 D、2,2,42. 如图所示,是的中线, , , 的周长和的周长差为( )
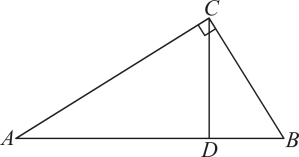
 A、 B、 C、 D、不确定3. 如图,中, , 于点D , 则下列结论不一定成立的是( )
A、 B、 C、 D、不确定3. 如图,中, , 于点D , 则下列结论不一定成立的是( ) A、 B、 C、 D、4. 将一副三角板按如图所示方式摆放,使有刻度的边互相垂直,则( )
A、 B、 C、 D、4. 将一副三角板按如图所示方式摆放,使有刻度的边互相垂直,则( )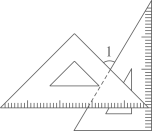 A、 B、 C、 D、5. 随着人们物质生活的提高,玩手机成为一种生活中不可缺少的东西,手机很方便携带,但唯一的缺点就是没有固定的支点,为了解决这一问题,某工厂研制生产了一种如图所示的手机支架把手机放在上面就可以方便地使用手机,这是利用了三角形的哪一个性质( )
A、 B、 C、 D、5. 随着人们物质生活的提高,玩手机成为一种生活中不可缺少的东西,手机很方便携带,但唯一的缺点就是没有固定的支点,为了解决这一问题,某工厂研制生产了一种如图所示的手机支架把手机放在上面就可以方便地使用手机,这是利用了三角形的哪一个性质( ) A、三角形两边之和大于第三边 B、三角形具有稳定性
A、三角形两边之和大于第三边 B、三角形具有稳定性
C、三角形的内角和是 D、直角三角形两个锐角互余6. 年北京冬奥会开幕式为世界奉献了一场精彩、简约、唯美、浪漫的中国文化盛宴,其中主火炬台的雪花状创意令人惊叹.如图是一个正六边形雪花状饰品,则它的每一个内角是( ) A、 B、 C、 D、7. 如图,在3×3的正方形方格中,每个小正方形方格的边长都为1.则和的关系是( )
A、 B、 C、 D、7. 如图,在3×3的正方形方格中,每个小正方形方格的边长都为1.则和的关系是( ) A、 B、 C、 D、8. 已知图中的两个三角形全等,则的度数是( )
A、 B、 C、 D、8. 已知图中的两个三角形全等,则的度数是( ) A、 B、 C、 D、9. 在和中,下列条件: , ; , ;
A、 B、 C、 D、9. 在和中,下列条件: , ; , ;, ; , .
能得出≌的序号是( ) A、 B、 C、 D、10. 如图,要用“”判定和全等的条件是( )
A、 B、 C、 D、10. 如图,要用“”判定和全等的条件是( ) A、 , B、 ,
A、 , B、 ,
C、 , D、 ,11. 如图,以的顶点为圆心,以长为半径作弧;再以顶点为圆心,以长为半径作弧,两弧交于点 , 连接 , , 若 , 的大小为( ) A、 B、 C、 D、12. 如图,一块三角形的玻璃打碎成四块,现要到玻璃店去配一块完全一样的玻璃,最简单的办法是( )
A、 B、 C、 D、12. 如图,一块三角形的玻璃打碎成四块,现要到玻璃店去配一块完全一样的玻璃,最简单的办法是( ) A、只带去 B、带去 C、带去 D、只带去
A、只带去 B、带去 C、带去 D、只带去二、填空题(本大题共6小题,共24.0分)
-
13. 在中, , 点是的重心,连接若 , 则长为 .14. 如图,是的高, . 若 , 则的度数是 .
 15. 如果正n边形的一个内角与外角的比是5:1,那么n= .16. 如图,D在边上, , , 则的度数为 .
15. 如果正n边形的一个内角与外角的比是5:1,那么n= .16. 如图,D在边上, , , 则的度数为 . 17. 如图,在和中, , , 若要用“斜边、直角边”直接证明≌ , 则还需补充条件: .
17. 如图,在和中, , , 若要用“斜边、直角边”直接证明≌ , 则还需补充条件: . 18. 如图,在四边形ABCD中,是边BC的中点,AE平分且 , 若 , , 则.
18. 如图,在四边形ABCD中,是边BC的中点,AE平分且 , 若 , , 则.
三、解答题(本大题共6小题,共40.0分。解答应写出文字说明,证明过程或演算步骤)
-
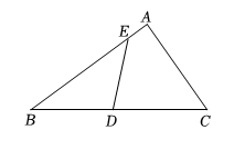
19. 如图,在中,点为中点,为上一点, , 若与四边形的周长相等,求的值.
 20. 如图,已知在中, , , 是边上的高,是的角平分线,求的度数.
20. 如图,已知在中, , , 是边上的高,是的角平分线,求的度数.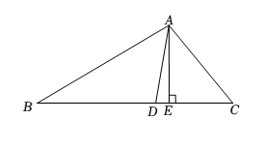 21. 如图,在五边形中, , , 分别平分 , , 求的度数.
21. 如图,在五边形中, , , 分别平分 , , 求的度数.