甘肃省张掖市高台县部分校联考2023-2024学年九年级上学期入学检测数学试题
试卷更新日期:2023-11-01 类型:开学考试
一、选择题(每小题3分,共30分)
-
1. 下列美丽的图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在数轴上表示不等式的解集,正确的是( )A、
2. 在数轴上表示不等式的解集,正确的是( )A、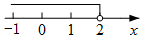 B、
B、 C、
C、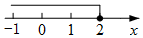 D、
D、 3. 下列等式从左到右的变形是因式分解的是( )A、b B、 C、 D、4. 下列分式中是最简分式的是( )A、 B、 C、 D、5. 一块三角形的草坪,现要在草坪上建一个凉亭供大家休息,要使凉亭到草坪三边的距离相等,凉亭的位置应选在( )A、三角形三条边的垂直平分线的交点 B、三角形三条角平分线的交点 C、三角形三条高所在直线的交点 D、三角形三条中线的交点6. 矩形、菱形、正方形都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线互相垂直且相等7. 如图,△OAB绕点O逆时针旋转85°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是( )
3. 下列等式从左到右的变形是因式分解的是( )A、b B、 C、 D、4. 下列分式中是最简分式的是( )A、 B、 C、 D、5. 一块三角形的草坪,现要在草坪上建一个凉亭供大家休息,要使凉亭到草坪三边的距离相等,凉亭的位置应选在( )A、三角形三条边的垂直平分线的交点 B、三角形三条角平分线的交点 C、三角形三条高所在直线的交点 D、三角形三条中线的交点6. 矩形、菱形、正方形都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线互相垂直且相等7. 如图,△OAB绕点O逆时针旋转85°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是( )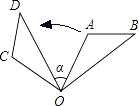 A、35° B、45° C、55° D、65°8. 函数y=2x-6的图象如图所示,当y>0时,x的取值范围为( )
A、35° B、45° C、55° D、65°8. 函数y=2x-6的图象如图所示,当y>0时,x的取值范围为( ) A、x>6 B、x<3 C、x>3 D、x<09. 如图,在Rt△ABC中,已知∠B=30°,AB=6cm,则BC的长为( )
A、x>6 B、x<3 C、x>3 D、x<09. 如图,在Rt△ABC中,已知∠B=30°,AB=6cm,则BC的长为( ) A、3cm B、4cm C、3cm D、4cm10. 如图所示,▱ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5,▱ABCD的周长( )
A、3cm B、4cm C、3cm D、4cm10. 如图所示,▱ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5,▱ABCD的周长( )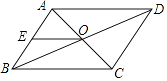 A、11 B、13 C、16 D、22
A、11 B、13 C、16 D、22二、填空题(本大题共8小题,共32分)
-
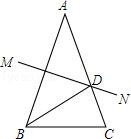
11. 分解因式: .12. 已知菱形的周长等于 , 两对角线长的比为 , 则较短对角线的长是 .13. 若一个多边形的每个外角都等于30°,则这个多边形的边数为 .14. 若代数式的值等于零,则x= .15. 某次知识竞赛共有20题,答对一题得10分,答错或不答扣5分,小华得分要超过120分,他至少要答对的题的个数为 .16. 如图,在△ABC 中,AB=AC,AB 的垂直平分线 MN 交 AC 于 D 点.若 BD 平分∠ABC, 则∠A=°.
 17. 如图,在中, , 将沿着BC的方向平移至 , 若平移的距离是3,则图中阴影部分的面积为 .
17. 如图,在中, , 将沿着BC的方向平移至 , 若平移的距离是3,则图中阴影部分的面积为 .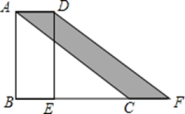 18. 如图,E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为25,DE=2,则AE的长为 .
18. 如图,E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为25,DE=2,则AE的长为 .
三、解答题(共88分)
-
19.(1)、分解因式:(2)、计算:20. 解分式方程: =1.21. 解不等式组:22. 先化简 , 再从0、、2、中取一个数代入求值。23. 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:

⑴画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标.
⑵画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2 , 并写出点A2的坐标.
24. 如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3 (1)、求证:BN=DN;(2)、求△ABC的周长25. 如图,在▱ABCD中,AE⊥BC于点E,CF⊥AB于点F,且AE=CF,求证:▱ABCD是菱形.
(1)、求证:BN=DN;(2)、求△ABC的周长25. 如图,在▱ABCD中,AE⊥BC于点E,CF⊥AB于点F,且AE=CF,求证:▱ABCD是菱形.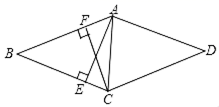 26. 如图,在△ABC中,AB=AC,D,E分别是线段BC,AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
26. 如图,在△ABC中,AB=AC,D,E分别是线段BC,AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.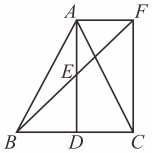 (1)、求证:△BDE≌△FAE;(2)、求证:四边形ADCF为矩形.27. 在争创文明城市的活动中,某市一“少年突击队”决定清运一堆重达100吨的垃圾,开工后附近居民主动参加到义务劳动中,使清运垃圾的速度比原计划提高了一倍,结果提前4小时完成,“少年突击队”原计划每小时清运垃圾多少吨?28. 如图,用硬纸板剪一个平行四边形ABCD,找到对角线交点O,用大头针在点O处将一根平放在平行四边形上的细直木条固定,并使细木条可以绕点O转动,拨动细木条,可随意停留在任意位置.
(1)、求证:△BDE≌△FAE;(2)、求证:四边形ADCF为矩形.27. 在争创文明城市的活动中,某市一“少年突击队”决定清运一堆重达100吨的垃圾,开工后附近居民主动参加到义务劳动中,使清运垃圾的速度比原计划提高了一倍,结果提前4小时完成,“少年突击队”原计划每小时清运垃圾多少吨?28. 如图,用硬纸板剪一个平行四边形ABCD,找到对角线交点O,用大头针在点O处将一根平放在平行四边形上的细直木条固定,并使细木条可以绕点O转动,拨动细木条,可随意停留在任意位置. (1)、木条把平行四边形ABCD分成了两部分,在拨动细木条的过程中,两部分的面积是否始终相等?答:(填“是”或“否”);(2)、木条与▱ABCD的边AD,BC相交于点E,F.
(1)、木条把平行四边形ABCD分成了两部分,在拨动细木条的过程中,两部分的面积是否始终相等?答:(填“是”或“否”);(2)、木条与▱ABCD的边AD,BC相交于点E,F.①请判断OE与OF是否始终相等,并说明理由;
②以A,E,C,F为顶点的四边形是平行四边形吗?为什么?