安徽省合肥市包河区四十八中滨湖分校2023-2024学年八年级上学期月考预测数学作业试卷
试卷更新日期:2023-11-01 类型:月考试卷
一、选择题(本大题共10小题,每小题3分,满分30分)
-
1. 点P(-3,4)所在的象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 在函数中,自变量x的取值范围是( )A、x≤3 B、x≥3 C、x≠3 D、x≤3且x≠03. 已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( )A、y=-x-1 B、y=-x-6 C、y=-x-2 D、y=-x+104. 点M ( -2,y1 )、N ( 3,y2 )是函数y=-x+b图象上两点,则y1与y2的大小关系( )A、y1>y2 B、y1<y2 C、y1=y2 D、无法确定5. 已知点P(1+m,2m+1)在y轴上,点Q(6-2n,4+n)在x轴上,则点M(m,n)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 已知一次函数y=ax—4与y=bx+2图象在x轴上相交于同一点,则的值是( )A、4 B、-2 C、 D、-7. 一根高18厘米的蜡烛点燃后剩余的高度h(厘米)与燃烧时间t(时)(0≤t≤6)的关系如表,已知平均每小时蜡烛燃掉3厘米,则蜡烛点燃后剩余的高度h(厘米)与燃烧时间t(时)(0≤t≤6)之间的关系式是( )
燃烧时间t(时)
0
1
2
3
4
剩余的高度h(厘米)
18
15
12
9
6
A、h=18-t B、h=18+t C、h=18-3t D、h=18+3t8. 甲、乙两位运动员在一段2000米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面200米,他们同时同向出发匀速前进,甲的速度是8米/秒,乙的速度是6米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是y米,比赛时间是x秒,当两人都到达终点计时结束,整个过程中y与x之间的函数图象是( )A、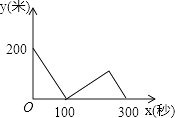 B、
B、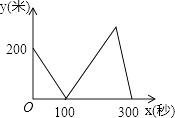 C、
C、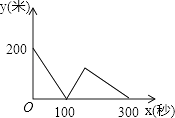 D、
D、 9. 两条直线y1=kx-b与y2=bx-k在同一坐标系中的图象可能是图中的( )A、
9. 两条直线y1=kx-b与y2=bx-k在同一坐标系中的图象可能是图中的( )A、 B、
B、 C、
C、 D、
D、 10. 在平面直角坐标系中,下列说法:
10. 在平面直角坐标系中,下列说法:①若点A(a,b)在坐标轴上,则ab=0;②若m为任意实数,则点(2,m2)一定在第一象限;③若点P到x轴的距离与到y轴的距离均为2,则符合条件的点P有2个;④已知点M(2,3),点N(-2,3),则MN∥x轴.其中正确的是( )
A、①④ B、②③ C、①③④ D、①②④二、填空题(本大题共5小题,每小题3分,满分15分)
-
11. 在平面直角坐标系中,点p(-3,-2)到x轴的距离是12. 已知一次函数y=(m-1)x|m|-2,则m=13. 若一次函数y=ax+3(a>0)的图象与两坐标轴围成的三角形的面积为3,则一次函数的表达式为14. 如图,在平面直角坐标系中,动点P按图中箭头所示方向从原点出发,第1次运动到点P1(1,1),第2次接着运动到点P2(2,0),第3次接着运动到点P3(3,-2),…,按这样的运动规律,点P2023的坐标是
 15. 设0<k<1,关于x的一次函数y=kx+(1-x).(1)、y随x的增大而;(2)、当1≤k≤2时y的最大值是(用含k的式子表示).
15. 设0<k<1,关于x的一次函数y=kx+(1-x).(1)、y随x的增大而;(2)、当1≤k≤2时y的最大值是(用含k的式子表示).三、(本大题共7小题,满分55分)
-
16. 已知2y+1与3x-3成正比例,且x=10时,y=4,求y与x之间的函数关系式。17. 如图,ΔABC在正方形网格中,若A(0,3),按要求回答下列问题:
 (1)、在图中建立正确的平面直角坐标系,并将ΔABC向右平移3个单位,再下平移3个单位得到△A1B1C1 , 画出平移后的三角形;(2)、计算ΔA1B1C1的面积;18. 观察下列由白色正方形和黑色正方形组成的图案,并解决下列问题.
(1)、在图中建立正确的平面直角坐标系,并将ΔABC向右平移3个单位,再下平移3个单位得到△A1B1C1 , 画出平移后的三角形;(2)、计算ΔA1B1C1的面积;18. 观察下列由白色正方形和黑色正方形组成的图案,并解决下列问题. (1)、图4中有个白色正方形;若图n中有m个白色正方形,则m与n的函数关系式是;(2)、若在图n中,白色正方形比灰色正方形多2023个,求n的值.19. 如图,一次函数y=(m-3)x-m+1图象分别与x轴正半轴、y轴负半轴相交于点A、B.
(1)、图4中有个白色正方形;若图n中有m个白色正方形,则m与n的函数关系式是;(2)、若在图n中,白色正方形比灰色正方形多2023个,求n的值.19. 如图,一次函数y=(m-3)x-m+1图象分别与x轴正半轴、y轴负半轴相交于点A、B. (1)、求m的取值范围;(2)、若该一次函数的图象向上平移4个单位长度后可得某正比例函数的图象,试求这个正比例函数的解析式。20. 在平面直角坐标系中,已知点M(m-2,2m-7),点N(n,3).(1)、若点M在x轴上,求m的值和点M坐标;(2)、若点M到x轴,y轴距离相等,求m的值;(3)、若MN∥y轴,且MN=2,求n的值.21. 为了更好放松心情,上周六,小红妈妈开车带着小红一家到外郊游,出发前汽车油箱内有一定量的油.行驶过程中油箱中剩余油量y(升)与行驶时间t(小时)的关系如表,请根据表格回答下列问题:
(1)、求m的取值范围;(2)、若该一次函数的图象向上平移4个单位长度后可得某正比例函数的图象,试求这个正比例函数的解析式。20. 在平面直角坐标系中,已知点M(m-2,2m-7),点N(n,3).(1)、若点M在x轴上,求m的值和点M坐标;(2)、若点M到x轴,y轴距离相等,求m的值;(3)、若MN∥y轴,且MN=2,求n的值.21. 为了更好放松心情,上周六,小红妈妈开车带着小红一家到外郊游,出发前汽车油箱内有一定量的油.行驶过程中油箱中剩余油量y(升)与行驶时间t(小时)的关系如表,请根据表格回答下列问题:时间/小时
0
1
2
3
4
5
油箱剩余油量/升
50
45
40
35
30
25
(1)、汽车行驶前油箱里有升汽油,汽车每小时耗油升;(2)、请写出y与t的关系式;(3)、当汽车行驶24小时时,油箱中还剩余多少升油?22. 小明的妈妈联合班级其他同学的家长去药店团购口罩.口罩原价是一包20元,由于家长们购买的数量比较多,药店老板决定给他们优惠,方式如下.方式一:每包口罩打九折;
方式二:如果购买的口罩不超过40包,则口罩按原价销售,如果购买的口罩超过40包,则超出的部分打八折销售.
设大家一共需要购买口罩x包.
(1)、口罩的总费用为y元,请分别求出两种方式的y与x的函数关系式;(2)、已知每位家长都要为孩子准备5包口罩,小明的妈妈该如何根据家长的人数选择优惠的方式?