北京市一零一中教育集团2023-2024学年九年级上学期月考数学试题
试卷更新日期:2023-11-01 类型:月考试卷
一、选择题(本题共16分,每小题2分)第1—8题均有四个选项,符合题意的只有一个.
-
1. 一元二次方程2x2+x-5=0的二次项系数、一次项系数、常数项分别是( )A、2,1,5 B、2,0,-5 C、2,1,-5 D、2,0,52. 由抛物线y=2x2 . 平移而得到抛物线y=2(x-1)2-2,下列平移正确的是( )A、先向左平移1个单位,再向上平移2个单位 B、先向左平移1个单位,再向下平移2个单位 C、先向右平移1个单位,再向上平移2个单位 D、先向右平移1个单位,再向下平移2个单位3. 如图,将一个正方形纸片沿图中虚线剪开,能拼成下列四个图形,其中是中心对称图形的是( )
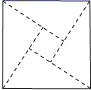 A、
A、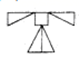 B、
B、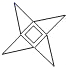 C、
C、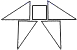 D、
D、 4. 用配方法解方程x2+4x+1=0,下列变形正确的是( )A、(x+2)2=3 B、(x+2)2=5 C、(x+2)2=-3 D、(x+2)2=-55. 如图,点A,B,C,D,O都在方格纸上,若△COD是由△AOB绕点O按逆时针方向旋转而得:则旋转的角度为( )
4. 用配方法解方程x2+4x+1=0,下列变形正确的是( )A、(x+2)2=3 B、(x+2)2=5 C、(x+2)2=-3 D、(x+2)2=-55. 如图,点A,B,C,D,O都在方格纸上,若△COD是由△AOB绕点O按逆时针方向旋转而得:则旋转的角度为( ) A、30° B、45° C、90° D、135°6. 若二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列四个选项正确的是( )
A、30° B、45° C、90° D、135°6. 若二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列四个选项正确的是( ) A、b>0,c<0 B、b<0,c<0 C、b>0,c>0 D、b<0,c>07. 如图,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,下列结论中一定正确的是( )
A、b>0,c<0 B、b<0,c<0 C、b>0,c>0 D、b<0,c>07. 如图,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,下列结论中一定正确的是( )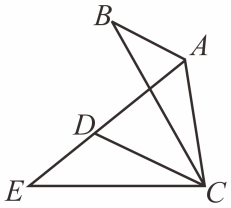 A、∠ABC=∠ADC B、CB=CD C、DE+DC=BC D、8. 在特定条件下,篮球赛中进攻球员投球后,篮球的运行轨迹是开口向下的抛物线的一部分.“盖帽”是一种常见的防守手段,防守队员在篮球上升阶段将球拦截即为“盖帽”,而防守队员在篮球下降阶段将球拦截则属“违规”.对于某次投篮而言,如果忽略其他因素的影响,篮球处于上升阶段的水平距离越长,则被“盖帽”的可能性越大,收集几次篮球比赛的数据之后,某球员投篮可以简化为下述数学模型:如图所示,该球员的投篮出手点为P,篮框中心点为Q,他可以选择让篮球在运行途中经过A,B,C,D四个点中的某一点并命中Q,忽略其他因素的影响,那么被“盖帽”的可能性最大的线路是( )
A、∠ABC=∠ADC B、CB=CD C、DE+DC=BC D、8. 在特定条件下,篮球赛中进攻球员投球后,篮球的运行轨迹是开口向下的抛物线的一部分.“盖帽”是一种常见的防守手段,防守队员在篮球上升阶段将球拦截即为“盖帽”,而防守队员在篮球下降阶段将球拦截则属“违规”.对于某次投篮而言,如果忽略其他因素的影响,篮球处于上升阶段的水平距离越长,则被“盖帽”的可能性越大,收集几次篮球比赛的数据之后,某球员投篮可以简化为下述数学模型:如图所示,该球员的投篮出手点为P,篮框中心点为Q,他可以选择让篮球在运行途中经过A,B,C,D四个点中的某一点并命中Q,忽略其他因素的影响,那么被“盖帽”的可能性最大的线路是( ) A、P→A→Q B、P→B→Q C、P→C→Q D、P→D→Ω
A、P→A→Q B、P→B→Q C、P→C→Q D、P→D→Ω二、填空题(本题共16分,每小题2分)
-
9. 在平面直角坐标系中,点P(3,-2)绕原点旋转180°后所得到的点的坐标为 .10. 已知x=1是方程:x2+bx-2=0的一个根,则b的值为 .11. 请你写出一个二次函数,其图象满足条件:①开口向下;②与 轴的交点坐标为 .此二次函数的解析式可以是12. 如图,将△ABC绕点A逆时针旋转55°得到△ADE,若∠E=70°且AD⊥BC于点F,则∠BAC的度数为 .
 13. 已知关于x的一元二次方程:x2+mx+m-1=0有两个相等的实数根,则m的值为 .14. 在二次函数y=ax2+bx+c(a≠0)中,y与x的部分对应值如表:
13. 已知关于x的一元二次方程:x2+mx+m-1=0有两个相等的实数根,则m的值为 .14. 在二次函数y=ax2+bx+c(a≠0)中,y与x的部分对应值如表:x
…-1
0
1
2
3
…
y
…
0
2
m
n
0…
则m,n的大小关系为mn.(填“>”“=”或“<”)
15. 电影《长津湖》一上映,第一天票房2.05亿元,若每天票房的平均增长率相同,三天后累计票房收入达10.53亿元,平均增长率记作x,方程可以列为 .16. 抛物线.y=-x2+2x+m交x轴于点A(a,0)和B(b,0),抛物线的顶点为D,下列四个结论:①抛物线过(2,m);②当m=0时,△ABD是等腰直角三角形;③a+b=4;④抛物线上有两点P(x1 , y1)和Q(x2 , y2),若:x1<1<x2 , 且x1+x2>2,则y1>y2 .
其中结论正确的序号是 .
三、解答题(本题共68分,第17题8分、18-20题4分、21、22题5分,23-25、27题6分,26题、28题7分)
-
17. 解方程:(1)、9x2=4;(2)、x2-x-6=0.18. 如图,正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系中,△OAB的三个顶点O(0,0),A(4,1),B(4,4)均在格点上.
 (1)、画出△OAB关于y轴对称的△OA1B1 , 直接写出点A1的坐标为 ▲ ;(2)、画出△OAB绕原点O旋转180°后得到的△OA2B2 .19. 已知a是方程2x2+7x-1=0的一个根,求代数式(a-2)2-3a(a+1)的值.20. 已知关于x的一元二次方程:3x2-(k+3)x+k=0.(1)、求证:该方程总有两个实数根;(2)、若该方程有一个根大于2,求k的取值范围.21. 已知抛物线y=2x2+bx+c过点(1,3)和(0,4)(1)、求该抛物线的解析式;(2)、直接写出该抛物线的顶点坐标 .22. 如图,△ABC是直角三角形,∠C=90°,将△ABC绕点C顺时针旋转90°.
(1)、画出△OAB关于y轴对称的△OA1B1 , 直接写出点A1的坐标为 ▲ ;(2)、画出△OAB绕原点O旋转180°后得到的△OA2B2 .19. 已知a是方程2x2+7x-1=0的一个根,求代数式(a-2)2-3a(a+1)的值.20. 已知关于x的一元二次方程:3x2-(k+3)x+k=0.(1)、求证:该方程总有两个实数根;(2)、若该方程有一个根大于2,求k的取值范围.21. 已知抛物线y=2x2+bx+c过点(1,3)和(0,4)(1)、求该抛物线的解析式;(2)、直接写出该抛物线的顶点坐标 .22. 如图,△ABC是直角三角形,∠C=90°,将△ABC绕点C顺时针旋转90°. (1)、试作出旋转后的△DCE,其中B与D是对应点;(2)、在作出的图形中,已知AB=5,BC=3,求BE的长.23. 已知二次函数.y=x2-2x-3.
(1)、试作出旋转后的△DCE,其中B与D是对应点;(2)、在作出的图形中,已知AB=5,BC=3,求BE的长.23. 已知二次函数.y=x2-2x-3. (1)、画出它的图象;(2)、当0<x≤4时,y的取值范围是 .(3)、直线y=kx+b与抛物线y=x2-2x-3交于点A,B,且点A在y轴上,点B在x轴的右半轴上,则不等式kx+b<x2-2x-3的解集为 .24. 体育课上,一名九年级学生测试扔实心球.已知实心球经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2米,当球运行的水平距离为4米时,到达最大高度为4米的B处(如图所示).
(1)、画出它的图象;(2)、当0<x≤4时,y的取值范围是 .(3)、直线y=kx+b与抛物线y=x2-2x-3交于点A,B,且点A在y轴上,点B在x轴的右半轴上,则不等式kx+b<x2-2x-3的解集为 .24. 体育课上,一名九年级学生测试扔实心球.已知实心球经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2米,当球运行的水平距离为4米时,到达最大高度为4米的B处(如图所示).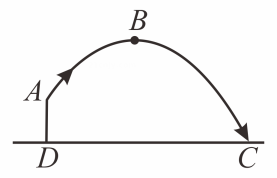 (1)、以D为原点,CD所在直线为x轴建立平面直角坐标系,在图中画出坐标系,点B的坐标为 ▲ ;(2)、请你计算该学生把实心球扔出多远?(结果保留根号)25. 正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)、以D为原点,CD所在直线为x轴建立平面直角坐标系,在图中画出坐标系,点B的坐标为 ▲ ;(2)、请你计算该学生把实心球扔出多远?(结果保留根号)25. 正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM. (1)、求证:EF=FM;(2)、当AE=2时,求EF的长.26. 在平面直角坐标系xOy中,点(1,m)和(2,n)在抛物线y=-x2+bx上.(1)、若m=1,求该抛物线的对称轴;(2)、若mn<0,设抛物线的对称轴为直线x=t,
(1)、求证:EF=FM;(2)、当AE=2时,求EF的长.26. 在平面直角坐标系xOy中,点(1,m)和(2,n)在抛物线y=-x2+bx上.(1)、若m=1,求该抛物线的对称轴;(2)、若mn<0,设抛物线的对称轴为直线x=t,①直接写出t的取值范围 ▲ ;
②已知点 在该抛物线上.将y1 , y2 , y3按从大到小排序,并说明理由.
27. 在Rt△ABC中,∠ABC=90°,∠BAC=α,D为AB的中点,过D作DE⊥AC于E,连接CD,F为CD的中点. (1)、图1中,BF与EF的数量关系是 , ∠BFE=(用含α的式子表示);(2)、将△ADE绕点A逆时针旋转至如图2所示位置,试判断(1)中的两个结论是否依然成立?若成立,请证明你的结论.28. 对于平面直角坐标系xOy内的点P和图形M,给出如下定义:如果点P绕原点O顺时旋转90°得到点 ,点 落在图形M上或图形M围成的区域内,那么称点P是图形M关于原点O的“伴随点”.
(1)、图1中,BF与EF的数量关系是 , ∠BFE=(用含α的式子表示);(2)、将△ADE绕点A逆时针旋转至如图2所示位置,试判断(1)中的两个结论是否依然成立?若成立,请证明你的结论.28. 对于平面直角坐标系xOy内的点P和图形M,给出如下定义:如果点P绕原点O顺时旋转90°得到点 ,点 落在图形M上或图形M围成的区域内,那么称点P是图形M关于原点O的“伴随点”.
已知点A(1,1),B(3,1),C(3,2).
(1)、在点P1(-2,0),P2(-1,1),P3(-1,2)中,点是线段AB关于原点O的“伴随点”;(2)、如果点D(m,2)是△ABC关于原点O的“伴随点”,直接写出m的取值范围;(3)、已知抛物线y=x2+bx+c的顶点坐标为(-1,n),其关于原点对称的抛物线上存在△ABC关于原点O的“伴随点”,求n的最大值和最小值.