山东省青岛市三十九中2023-2024学年九年级上学期月考数学试卷（10月份）
试卷更新日期：2023-11-01 类型：月考试卷
一、选择题：（每小题3分，共24分）
-
1. 下列方程中，属于一元二次方程的是（ ）A、ax2+bx+c＝0 B、x2+3＝ C、2y-x＝1 D、x2＝2x-12. 在复习特殊的平行四边形时．某小组同学画出了如图关系图，组内一名同学在箭头处填写了它们之间转换的条件，其中填写错误的是（ ）
A、①，对角相等 B、③，有一组邻边相等 C、②，对角线互相垂直 D、④，有一个角是直角3. 观察下列表格，估计一元二次方程x2+3x-5＝0的正数解在（ ）x
-1
0
1
2
3
4
x2+3x-5
-7
-5
-1
5
13
23
A、-1和0之间 B、0和1之间 C、1和2之间 D、2和3之间4. 小明用四根长度相同的木条制作了能够活动的菱形学具，他先活动学具成为图1所示菱形，并测得∠B＝60°，对角线AC=5，接着活动学具成为图2所示正方形，则图2中对角线AC的长为（ ）
A、5 B、 C、10 D、155. 如图，在菱形ABCD中摆放了一副三角板．等腰直角三角板DEF的一条直角边DE在菱形边AD上，直角顶点E为AD的中点，含30°角的直角三角板的斜边GB在菱形ABCD的边AB上．∠CDF的度数等于（ ）
A、55° B、65° C、75° D、85°6. 用12m长的铁丝围成一个一边靠墙的长方形场地，使该场地的面积为20m2 ， 并且在垂直于墙的一边开一个1m长的小门（用其它材料），若设垂直于墙的一边长为xm ， 那么可列方程为（ ）
A、 B、 C、x（12-2x+1）＝20 D、x（12-2x-1）＝207. 如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，OH＝4，若菱形ABCD的面积为32 ， 则CD的长为（ ）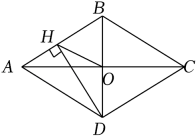
A、4 B、4 C、8 D、88. 如图，在边长为2的等边三角形ABC的外侧作正方形ABED，过点D作DF⊥BC，垂足为F，则DF的长为（ ）
A、2+2 B、5- C、3- D、+1二、填空题：（每小题3分，共24分）
-
9. 一元二次方程x2＝5x的解为 ．10. 顺次连接矩形各边中点，形成的四边形是 ．11. 一元二次方程x2-4x+2＝0配方后得（x-2）2＝n ， 则n的值为 ．12. 电影《长津湖》于2021年9月30日在中国大陆上映，某地第一天票房约2亿元，以后每天票房按相同的增长率增长，三天后票房收入累计达7亿元，若把增长率记作x ， 则方程可以列为 ．13. 若关于x的一元二次方程kx2-2x-1＝0有两个实数根，则k的取值范围是 ．14. 如图所示，在矩形ABCD中，DE⊥AC于E，∠EDC：∠EDA=1：3，且AC＝10，则DE的长度是 ．
15. 如图，四边形ABCD是菱形，AB＝10，AC：BD=4：3，DH⊥AB于H，则DH等于 ．
16. 如图，正方形ABCD的边长为10，E为AD的中点，连接CE，过点B作BF⊥CE交CD于点F，垂足为G，连接AG、DG，下列结论：①BF＝CE；②AG＝CD；④EG＝2；⑤DG＝；其中正确结论有（填写序号）．
三、解答题：（本题共72分）
-
17. 作图题
用圆规、直尺作图，不写作法，但要保留作图痕迹．
已知：线段a
求作：矩形ABCD，使它的对角线AC、BD相交于O点，且AC＝a，∠AOB=60°
18. 解方程：(1)、x 2 -1＝4x（公式法）；(2)、2x 2 -7x+3＝0（配方法）；(3)、3x（x-2）＝4-x 2 ；(4)、4（x+2） 2 ＝（3x-1） 2 ．19. 已知关于x的一元二次方程x2-（k+1）x+2k-3＝0．(1)、求证：无论k为何实数，方程总有两个不相等的实数根；(2)、等腰三角形ABC中，AB＝3，若AC、BC为方程x2-（k+1）x+2k-3＝0的两个实数根，求k的值．20. 某社区在开展“美化社区，幸福家园”活动中，计划利用如图所示的直角墙角（阴影部分，两边足够长），用50米长的篱笆围成一个矩形花园ABCD（篱笆只围AB ， AD两边）．若在直角墙角内点P处有一棵桂花树，且与墙BC ， CD的距离分别是10米，30米，要将这棵树围在矩形花园内（含边界，不考虑树的粗细），则花园的面积能否为625平方米？若能，求出AB的值；若不能，请说明理由．
21. 平行四边形ABCD的两条对角线交于点O，E，F分别为BO，DO的中点，连接AF，AE，CF，CE。
(1)、判断四边形AECF的形状并说明理由；(2)、当AC与BD满足怎样的数量关系时，四边形AECF是矩形？为什么？22. 某景区5月份的游客人数比4月份增加60%，6月份的游客人数比5月份减少了10%．(1)、设该景区4月份的游客人数为a万人，请用含a的代数式填表：月份
4月
5月
6月
游客人数/万人
a
③
④
(2)、求该景区5月份、6月份游客人数的月平均增长率；(3)、景区特色商品营销店推出一款成本价为40元的文化衫，如果按每件60元销售，每天可卖出20件．通过市场调查发现，每件售价每降低1元，日销售量增加2件．若日利润保持不变，商家想尽快销售完该款商品，每件售价应定为多少元？23. 如图所示，在平面直角坐标系中，O为坐标原点， 四边形ABCO是菱形 ， 点A的坐标为（-3，4），点C在x轴正半轴上，直线AC交y轴于点M，AB边交y轴于点H．
(1)、求直线AC的函数解析式及MH的长；(2)、连接BM，动点P从点A出发，沿折线A→B→C方向以每秒1个单位的速度向终点C匀速运动（S≠0），设的面积为S（），点P的运动时间为t秒，求S与t之间的函数关系式，并写出自变量t的取值范围；(3)、在（2）的情况下，当点P在线段AB上运动时，是否存在以BM为腰的等腰三角形PBM？若存在，直接写出t的值；如不存在，请说明理由。