期中微专题提分精炼：用频率估计概率-2023-2024学年北师大版九年级（上）数学

试卷更新日期：2023-10-31 类型：复习试卷

进入出卷网下载

一、选择题

1. 为了解某地区九年级男生的身高情况，随机抽取了该地区200名九年级男生，他们的身高 $x (c m)$ 统计如下：

组别 $(c m)$

$x < 160$

$160 \leq x < 170$

$170 \leq x < 180$

$x \geq 180$

人数

10

m

n

42

根据以上结果，抽查该地区一名九年级男生，估计他的身高不低于180cm的概率是（　　）

A、0.42 B、0.21 C、0.79 D、与m，n的取值有关

查看试题解析

2. 如表是一位同学在罚球线上投篮的试验结果，根据表中数据回答下列问题：

投篮次数 $(n)$	50	100	150	200	250	300	500
投中次数 $(m)$	28	60	78	104	124	153	252

估计这位同学投篮一次，投中的概率约是（精确到0.1）（）

A、0.4 B、0.5 C、0.55 D、0.6

查看试题解析

3. 在抛掷一枚质地均匀的硬币的实验中，第100次抛掷时，反面朝上的概率是（）

A、 $\frac{1}{100}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、不确定

查看试题解析
4. 某小组做“用频率估计概率”的实验时，绘出某一结果出现的频率折线图.如图所示，则符合这一结果的实验可能是(　　)

A、抛一枚硬币，出现正面朝上 B、从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球 C、一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃 D、掷一个正六面体的骰子，出现3点朝上

查看试题解析
5. 已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有2个，黑球有n个.随机地从袋子中摸出一个球，记录下颜色后，放回袋子中并摇匀.经过大量重复试验发现摸出白球的频率稳定在0.4附近，则n的值为（）

A、2 B、3 C、4 D、5

查看试题解析
6. 某射击运动员在同一条件下射击，结果如下表所示：
射击总次数n
10
20
50
100
200
500
1000
击中靶心的次数m
8
17
40
79
158
390
780
击中靶心的频率
0.8
0.85
0.8
0.79
0.79
0.78
0.78
根据频率的稳定性，这名运动员射击一次击中靶心的概率约是（）

A、0.78 B、0.79 C、0.8 D、0.85

查看试题解析
7. 已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有9个，黑球有n个，若随机地从袋子中摸出一个球，记录下颜色后，放回袋子中并摇匀，经过大量重复试验发现摸出黑球的频率稳定在0.4附近，则n的值为（　　）

A、5 B、6 C、7 D、8

查看试题解析
8. 在一个不透明的口袋中，放置3个黄球，1个红球和 $n$ 个蓝球，这些小球除颜色外其余均相同，课外兴趣小组每次摸出一个球记录下颜色后再放回，并且统计了蓝球出现的频率（如图所示），则 $n$ 的值最可能是（）

A、4 B、5 C、6 D、7

查看试题解析
9. 如图是用计算机模拟抛掷一枚啤酒瓶盖试验的结果，下面有四个推断，其中最合理的（）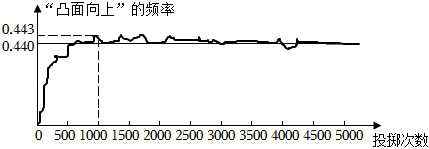

A、当投掷次数是1000时，计算机记录“凸面向上”的频率是0.443，所以“凸面向上”的概率是0.443 B、若再次用计算机模拟此实验，则当投掷次数为1000时，“凸面向上”的频率一定是0.443 C、随着试验次数的增加，“凸面向上”的频率总在0.440附近摆动，显示出一定的稳定性，可以估计“凸面向上”的概率是0.440 D、当投掷次数是5000次以上时，“凸面向上”的频率一定是0.40.

查看试题解析
10. 一个袋子中装有12个球（袋中每个球除颜色外其余都相同）．某活动小组想估计袋子中红球的个数，分10个组进行摸球试验，每一组做400次试验，汇总后，摸到红球的次数为 3000次．请你估计袋中红球接近（）

A、3 B、4 C、6 D、9

查看试题解析

二、填空题

11. 在一个不透明的布袋中，有红、蓝两种颜色的球若干个，它们除了颜色外其余都相同.小甘进行以下重复实验：每摸出一个球，记录下颜色然后放回摇匀，实验数据如下表：
实验次数
100
200
300
400
摸出红球
78
161
238
320
则从布袋中摸出一个球是红球的概率是.

查看试题解析
12. 一个不透明的口袋中有红球和黑球共若干个，这些球除颜色外都相同，每次摸出1个球，进行大量的球试验后，发现摸到红球的频率在0.4附近摆动，据此估计摸到红球的概率为．

查看试题解析
13. 一个不透明的布袋中，装有红、黄、白三种只有颜色不同的小球，其中红色小球有8个，黄、白色小球的数目相等，为估计袋中黄色小球的数目，每次将袋中小球搅匀后摸出一个小球记下颜色，再次搅匀 $\dots \dots$ 多次试验发现摸到红球的频率是 $\frac{1}{6}$ ，则估计黄色小球的数目是个。

查看试题解析
14. 在一个不透明的袋子中放有m个球，其中有6个红球，这些球除颜色外完全相同．若每次把球充分搅匀后，任意摸出一球记下颜色后再放回袋子，通过大量重复试验后，发现摸到红球的频率稳定在0.3左右，则m的值约为．

查看试题解析
15. 从一个不透明的口袋中随机摸出1个球，再放回袋中，不断重复上述过程，一共摸了150次，其中有50次摸到黑球，已知口袋中仅有黑球10个和白球若干个，这些球除颜色外，其他都一样，由此估计口袋中有个白球．

查看试题解析

三、解答题

16. 在一个不透明的袋中装有材质、大小完全相同的红球和黑球共100个，小明每次摇匀后随机从袋中摸出一个球，记录颜色后放回袋中，通过大量重复摸球试验后发现，摸到红球的频率稳定在0.85左右，估计袋中红球的个数．

查看试题解析
17. 南校区本学期对初三学生体育选考项目---引体向上（仅男生项目）进行抽样调查，已知完成15个可以拿到100分，完成23个为最高120分，A表示学生做引体向上23个或以上，B表示做15-22个，C表示做10-14个，D表示做9个或9个以下.根据调查结果绘制了不完整的统计图.
成绩
频数（人数）
频率
A
28
x
B
14
0.2
C
m
0.3
D
n
y

(1)、抽样学生数为人，x= ， y=；

(2)、补全条形统计图；

(3)、若南校区初三共有720名学生，男女比例为7：5，请估计一共有多少学生可以拿到100分及以上？

查看试题解析

四、综合题

18. 在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：
摸球的次数n
100
200
300
500
800
1000
摸到黑球的次数m
$\begin{array}{l} 65 \end{array}$
$\begin{array}{l} 118 \end{array}$
$\begin{array}{l} 189 \end{array}$
$\begin{array}{l} 310 \end{array}$
$\begin{array}{l} 482 \end{array}$
$\begin{array}{l} 602 \end{array}$
摸到黑球的频率 $\frac{m}{n}$
$\begin{array}{l} a \end{array}$
$\begin{array}{l} 0.59 \end{array}$
$\begin{array}{l} 0.63 \end{array}$
$\begin{array}{l} 0.62 \end{array}$
$\begin{array}{l} 0.603 \end{array}$
$\begin{array}{l} 0.602 \end{array}$

(1)、填空：a= ；当n很大时，摸到黑球的频率将会趋近(精确到0.1)；

(2)、某小组成员从袋中拿出1个黑球，3个白球放入一个新的不透明袋子中，随机摸出两个球，请你用列表或树状图的方法求出随机摸出的两个球颜色不同的概率．

查看试题解析
19. 小颖和小红两位同学在学习“概率”时，做掷骰子（质地均匀的正方体）实验．

(1)、他们在一次实验中共掷骰子60次，试验的结果如下：

朝上的点数

1

2

3

4

5

6

出现的次数

7

9

6

8

20

10

①填空：此次实验中“5点朝上”的频率为 ▲ ；

②小红说：“根据实验，出现5点朝上的概率最大．”她的说法正确吗？为什么？

(2)、小颖和小红在实验中如果各掷一枚骰子，那么两枚骰子朝上的点数之和为多少时的概率最大？试用列表或画树状图的方法加以说明，并求出其最大概率．

查看试题解析

20. 在一个不透明的袋子里装有只有颜色不同的红、白两种颜色的球共5个．某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色．再把它放回袋中．不断重复，下表是活动中的一组统计数据：

摸球的次数n	100	150	300	500	800	1000
摸到白球的次数m	54	98	174	295	484	602
摸到白球的频率 $\frac{m}{n}$	0.54	0.65	0.58	0.59	0.603	0.602

(1)、请估计，当n很大时，摸到白球的概率接近（结果精确到0.1）．

(2)、试估算口袋中白球的个数．

(3)、在-次摸球游戏中，小明发现先后摸两次球（第一次放回），第一次摸到白球的概率为

\frac{3}{5}

，第二次摸到白球的概率也为

\frac{3}{5}

，那么两次都摸到白球的概率为

\frac{3}{5}

\frac{3}{5}

\frac{9}{25}

，根据以上信息，求事件A （第一次摸到红球，第二次摸到白球）的概率．

查看试题解析

组别 $(c m)$	$x < 160$	$160 \leq x < 170$	$170 \leq x < 180$	$x \geq 180$
人数	10	m	n	42

射击总次数n	10	20	50	100	200	500	1000
击中靶心的次数m	8	17	40	79	158	390	780
击中靶心的频率	0.8	0.85	0.8	0.79	0.79	0.78	0.78

摸球的次数n	100	200	300	500	800	1000
摸到黑球的次数m	$\begin{array}{l} 65 \end{array}$	$\begin{array}{l} 118 \end{array}$	$\begin{array}{l} 189 \end{array}$	$\begin{array}{l} 310 \end{array}$	$\begin{array}{l} 482 \end{array}$	$\begin{array}{l} 602 \end{array}$
摸到黑球的频率 $\frac{m}{n}$	$\begin{array}{l} a \end{array}$	$\begin{array}{l} 0.59 \end{array}$	$\begin{array}{l} 0.63 \end{array}$	$\begin{array}{l} 0.62 \end{array}$	$\begin{array}{l} 0.603 \end{array}$	$\begin{array}{l} 0.602 \end{array}$

实验次数	100	200	300	400
摸出红球	78	161	238	320

成绩	频数（人数）	频率
A	28	x
B	14	0.2
C	m	0.3
D	n	y

朝上的点数	1	2	3	4	5	6
出现的次数	7	9	6	8	20	10