期中微专题提分精炼：一元二次方程的应用-2023-2024学年北师大版九年级（上）数学

试卷更新日期：2023-10-31 类型：复习试卷

进入出卷网下载

一、选择题

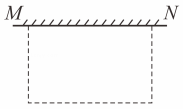
1. 要组织一次排球邀请赛，参赛的每两个队之间比赛一场，根据场地和时间等条件，赛程计划安排 $7$ 天，每天安排 $4$ 场比赛，设比赛组织者应邀请 $x$ 个队参赛，则 $x$ 满足的关系式为（）

A、 $\frac{1}{2} x (x + 1) = 28$ B、 $x (x - 1) = 28$ C、 $x (x + 1) = 28$ D、 $\frac{1}{2} x (x - 1) = 28$

查看试题解析
2. 空地上有一段长为20米的旧墙 $M N$ ，一边利用旧墙，其他三边利用木栏围成一个矩形菜园如图所示，已知木栏总长为40米，所围成的菜园面积为198.设垂直于旧墙的一边长为 $x$ 米，下列正确的是（）

A、由题意，得 $- x^{2} + 40 x = 198$ B、 $x$ 的取值范围为 $x < 20$ C、只有一种围法 D、只有两种围法

查看试题解析
3. 我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽.每株脚钱三文足，无钱准与一株椽.”其大意为：现请人代买一批椽，这批椽的价钱为6210文.如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱.根据题意可列方程 $3 x (x - 1) = 6210$ ，其中 $x$ 表示（）

A、剩余椽的数量 B、这批椽的数量 C、剩余椽的运费 D、每株椽的价钱

查看试题解析
4. 进入 $7$ 月以来，某大型商场前三周的营业收入持续上涨，若 $7$ 月第 $1$ 周营业收入为 $1.3$ 亿元， $7$ 月第 $3$ 周的营业收入为 $2$ 亿元，设平均每周的增长率为 $x$ ，则可列方程为（）

A、 $1.3 (1 + x) = 2$ B、 $1.3 (1 + x)^{2} = 2$
C、 $1.3 (1 + 2 x) = 2$ D、 $1.3 + 1.3 (1 + x) + 1.3 (1 + x)^{2} = 2$

查看试题解析
5. 某超市一月份的营业额为100万元，已知第一季度的总营业额共500万元，如果平均每月增长率为x，则由题意列方程应为（）

A、100+100(1+x)+100(1+x)²=500 B、100(1+x)²=500 C、100+100(1+x)²=500 D、100(1+x)=500

查看试题解析
6. 电影《满江红》于2023年1月22日在中国大陆上映，某地第一天票房约2亿元，以后每天票房按相同的增长率增长，三天后票房收入累计达7亿元，若把增长率记作x ，则方程可以列为（）

A、 $2 (1 + x) = 7$ B、 $2 (1 + x)^{2} = 7$ C、 $2 + 2 (1 + x)^{2} = 7$ D、 $2 + 2 (1 + x) + 2 (1 + x)^{2} = 7$

查看试题解析
7. 地理生物中考前，有一个学习小组有 $x$ 人，每两人都互相送对方寄语卡片一张，为彼此加油打气，全组共赠送了56张卡片，根据题意列出的方程是（）

A、 $\frac{1}{2} x$ （ $x$ ＋1）＝56 B、 $\frac{1}{2} x$ （ $x$ －1）＝56 C、 $x$ （ $x$ －1）＝56 D、 $x$ （ $x$ ＋1）＝56

查看试题解析
8. 要组织一次足球邀请赛，参赛的每两个队之间都要比赛一场.计划安排28场比赛，应邀请多少个队参赛（）

A、6 B、7 C、8 D、9

查看试题解析
9. 为了迎接校庆，初三年级组织乒乓球比赛，赛制为单循环形式（每两个选手之间都必须赛一场），全年级共进行了28场比赛，这次参赛的选手有（）

A、7位 B、8位 C、9位 D、10位

查看试题解析
10. 某超市购进一批商品，单价40元．经市场调查，销售定价为52元时，可售出180个，定价每增加1元，销售量减少10个，因受库存的影响，每批次进货个数不得超过180个，超市若将准备获利2000元，则定价为多少元？（）

A、50 B、60 C、50或60 D、100

查看试题解析

二、填空题

11. 为了加快数字化城市建设，某市计划新建一批智能充电桩，第一个月新建了301个充电桩，第三个月新建了500个充电桩，设该市新建智能充电桩个数的月平均增长率为 $x$ ，根据题意，可列出方程.

查看试题解析
12. 进入 $7$ 月以来，某大型商场前三周的营业收入持续上涨，若 $7$ 月第 $1$ 周营业收入为 $1.3$ 亿元， $7$ 月第 $3$ 周的营业收入为 $2$ 亿元，设平均每周的增长率为 $x$ ，则可列方程为．

查看试题解析
13. 公园原有一块正方形空地，后来从这块空地上划出部分区域栽种鲜花（阴影部分），原空地一边减少了3m ，另一边减少了2m ，剩余空地面积为56m² ，设正方形空地原来的边长为xm ，则可列方程为．

查看试题解析
14. 我国南宋数学家杨辉所著《田亩比类乘除捷法》中记载了这样一道题：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步．”其大意为：一个矩形的面积为864平方步，宽比长少12步，问宽和长各多少步？设矩形的宽为x步，根据题意，可列方程为．

查看试题解析
15. 某校九(1)班的学生互赠新年贺卡，共用去1560张贺卡，则九(1)班有名学生．

查看试题解析

三、解答题

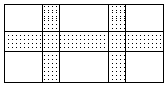
16. 如下图所示，在宽为20m，长为32m的矩形耕地上，修筑同样宽的三条道路（互相垂直），把耕地分成大小不等的六块试验田，要使试验田的面积为 $570 m^{2}$ ，道路应为多宽？

查看试题解析
17. 某连锁超市花2000元购进一批糖果，按80%的利润定价无人购买，决定降价出售，但仍无人购买，结果又一次降价后才售完，销售此糖果共获利916元，若两次降价的百分率相同，问每次降价的百分率是多少？

查看试题解析
18. 疫情期间，学校利用一段长度仅为5米的围墙搭建一个矩形临时隔离点 $A B C D$ ，如图所示，它的另外三边所围的总长度是10米，矩形隔离点的面积为12平方米，求 $A B$ 的长度.

查看试题解析
19. 西瓜经营户以2元/千克的价格购入一批小型西瓜，以3元/千克的价格出售，每天可以售出200千克，为了促销减少库存，该经营户决定降价销售，经调查发现，这种小型西瓜每降价0.1元/千克，每天可多售出40千克，该经销户想每天盈利224元，应将每千克小型西瓜的售价降多少元？

查看试题解析

四、综合题

20. 某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了迎接“双11”节，扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件.设每件降价x元.

(1)、降价后每件利润元，商场能售出件.

(2)、要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元？

查看试题解析
21. 芯片目前是全球紧缺资源，市政府通过资本招商引进“芯屏汽合、集终生智”等优势产业，发展新兴产业.某芯片公司，引进了一条内存芯片生产线，开工第一季度生产200万个，第三季度生产288万个.试回答下列问题：

(1)、已知每季度生产量的平均增长率相等，求前三季度生产量的平均增长率；

(2)、经调查发现，1条生产线最大产能是600万个/季度，若每增加1条生产线，每条生产线的最大产能将减少20万个/季度.现该公司要保证每季度生产内存芯片2600万个，在增加产能同时又要节省投入成本的条件下（生产线越多，投入成本越大），应该再增加几条生产线？

查看试题解析
22. 某水果商场经销一种高档水果，原价每千克50元．连续两次降价后每千克32元，若每次下降的百分率相同．

(1)、求每次下降的百分率；

(2)、若每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，商场决定采取适当的涨价措施，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，那么每千克应涨价多少元？

查看试题解析
23. 如图，某小区矩形绿地的长、宽分别为35m和15m，现计划对其进行扩充，将绿地的长宽增加相同的长度后，得到一个新的矩形绿地．

(1)、若扩充后的矩形绿地面积为 $800 m^{2}$ ，求新的矩形绿地长与宽．

(2)、若扩充后，实地测量发现新的矩形绿地的长宽之比为5：3，求新的矩形绿地面积．

查看试题解析