【北师大版·数学】2024年中考一轮复习之相似三角形的判定与性质
试卷更新日期:2023-10-30 类型:一轮复习
一、选择题
-
1. 如图,在中, , , 下列结论一定正确的是( )
 A、 B、 C、 D、2. 如图,在△ABC中,DE∥BC,若 , 则△ADE与△ABC的面积之比为( )
A、 B、 C、 D、2. 如图,在△ABC中,DE∥BC,若 , 则△ADE与△ABC的面积之比为( )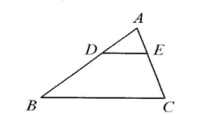 A、 B、 C、 D、3. 如图,在中,点D,E分别在上, , 如果 , 那么( )
A、 B、 C、 D、3. 如图,在中,点D,E分别在上, , 如果 , 那么( ) A、 B、 C、 D、4. 如图, , 且 , , 的长为( )
A、 B、 C、 D、4. 如图, , 且 , , 的长为( ) A、10 B、9 C、14 D、125. 如图,线段 , 相交于点 , , 若 , , , 则的长是( )
A、10 B、9 C、14 D、125. 如图,线段 , 相交于点 , , 若 , , , 则的长是( ) A、3 B、4 C、5 D、66. 如图,与位似,点O为位似中心.已知 , 的周长为4,则的周长为( )
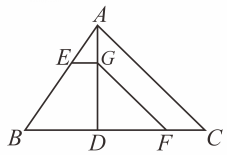
A、3 B、4 C、5 D、66. 如图,与位似,点O为位似中心.已知 , 的周长为4,则的周长为( ) A、8 B、12 C、16 D、207. 中过点A作垂线 , 将三角形面积分为两部分,求的值( )A、十三分之六 B、九分之五 C、五分之二 D、十二分之七8. 如图,中, , 点D是AB的中点,连接CD,过点B作 , 分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,下列结论正确的是( )
A、8 B、12 C、16 D、207. 中过点A作垂线 , 将三角形面积分为两部分,求的值( )A、十三分之六 B、九分之五 C、五分之二 D、十二分之七8. 如图,中, , 点D是AB的中点,连接CD,过点B作 , 分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,下列结论正确的是( ) A、 B、 C、AB D、
A、 B、 C、AB D、二、填空题
-
9. 如图,已知两点A(2,0),B(0,4),且∠1=∠2,则点C的坐标是
 10. 如图是步枪在瞄准时的示意图,从眼睛到准星的距离OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,则眼睛到目标的距离OF为m.
10. 如图是步枪在瞄准时的示意图,从眼睛到准星的距离OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,则眼睛到目标的距离OF为m. 11. 如图,线段 , 为的中点,射线于点 , 于点 , , 分别是射线 , 上的动点,且满足.
11. 如图,线段 , 为的中点,射线于点 , 于点 , , 分别是射线 , 上的动点,且满足.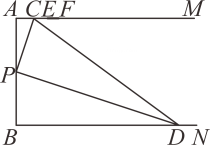
⑴的值为;
⑵长为1的线段在射线上,且 , 若动点在线段上时(包括端点),则就会发光,写出此时的一个整数值:.(答案不唯一)
12. 如图所示的网格是正方形网格,则∠BAC+∠CDE=°(点A , B , C , D , E是网格线交点). 13. 如图,小明借助太阳光线测量树高.在早上8时小明测得树的影长为 , 下午3时又测得该树的影长为 , 且这两次太阳光线刚好互相垂直,则树高为.
13. 如图,小明借助太阳光线测量树高.在早上8时小明测得树的影长为 , 下午3时又测得该树的影长为 , 且这两次太阳光线刚好互相垂直,则树高为.
三、解答题
-
14. 如图,为中边上的一点, , 若 , , , 求的长.
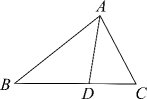 15. 如图,已知 .求证: .
15. 如图,已知 .求证: .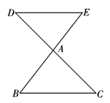 16. 如图,为了测量池塘的宽 ,在岸边找到点 ,测得 ,在 的延长线上找一点 ,测得 ,过点 作 交 的延长线于 ,测出 ,则池塘的宽 为多少 ?
16. 如图,为了测量池塘的宽 ,在岸边找到点 ,测得 ,在 的延长线上找一点 ,测得 ,过点 作 交 的延长线于 ,测出 ,则池塘的宽 为多少 ?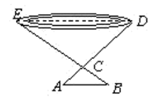 17. 如图,在中,是边上一点.
17. 如图,在中,是边上一点.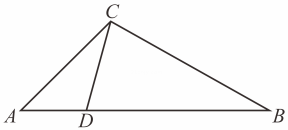 (1)、当时,
(1)、当时,①求证:;
②若 , , 求的长;
(2)、已知 , 若 , 求的长.18. 如图,在和中,已知 , . (1)、求证: .(2)、若S,求的长.19. 如图,为上一点,若 , , 求证: .
(1)、求证: .(2)、若S,求的长.19. 如图,为上一点,若 , , 求证: .
四、综合题
-
20. 如图,在△ABC中,D,E分别是边AB,AC上的点,连结DE, ∠ADE= ∠ACB.
 (1)、求证:△ADE∽△ACB.(2)、如果E是AC的中点,AD=8,AB=10,求AE的长.21. 如图,BE是△ABC的角平分线,延长BE至D,使得BC=CD.
(1)、求证:△ADE∽△ACB.(2)、如果E是AC的中点,AD=8,AB=10,求AE的长.21. 如图,BE是△ABC的角平分线,延长BE至D,使得BC=CD.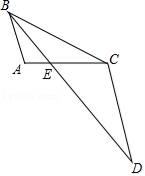 (1)、求证:△AEB∽△CED;(2)、若AB=2,BC=4,AE=1,求CE长.
(1)、求证:△AEB∽△CED;(2)、若AB=2,BC=4,AE=1,求CE长.
22. 已知:如图, 中, , , 为 边上一点, . (1)、求证: .(2)、若 交 于点 ,请再写出另一个与 相似的三角形,并直接写出 长.
(1)、求证: .(2)、若 交 于点 ,请再写出另一个与 相似的三角形,并直接写出 长.
23. 如图,在中,于点D,点E在上(不与点A,B重合),连接交于点F,. (1)、求证:.(2)、若 , , , 求的长.24. 如图,P为AB上一点,∠A=∠CPD=∠B,连接CD.
(1)、求证:.(2)、若 , , , 求的长.24. 如图,P为AB上一点,∠A=∠CPD=∠B,连接CD. (1)、求证:△ACP∽△BPD(2)、若AP=3,AB=9,AC=8,求BD的长.
(1)、求证:△ACP∽△BPD(2)、若AP=3,AB=9,AC=8,求BD的长.

