河北省石家庄市赵县2023-2024学年八年级上学期第一次测评数学试卷
试卷更新日期：2023-10-30 类型：月考试卷
一、选择题（本大题有16个小题，共42分．1～10小题各3分，11～16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的，请用2B铅笔将正确选项涂黑）
-
1. 下列关于三角形的分类，正确的是（ ）A、
B、
C、
D、
2. 下列说法正确的是（ ）
A、全等三角形是指形状相同的三角形 B、全等三角形是指面积相等的两个三角形 C、全等三角形的周长和面积相等 D、所有等边三角形是全等三角形3. 下列各组长度的线段为边，能构成三角形的是（ ）A、1，2，3 B、3，4，5 C、4，5，11 D、6，3，34. 下列各组图形中，BD是△ABC的高的图形是（ ）A、
B、
C、
D、
5. 如图，△ABC≌△DEC ， B、C、D在同一直线上，且CE=5，AC＝7，则BD长（ ）
A、12 B、7 C、2 D、146. 下列说法正确的是（ ）A、两个等边三角形一定是全等图形 B、两个全等图形面积一定相等 C、形状相同的两个图形一定全等 D、两个正方形一定是全等图形7. 如图，△ABC≌△ADE ， 且AE∥BD ， ∠BAD=96°，则∠BAC的度数的值为（ ）
A、84° B、42° C、48° D、60°8. 如图所示，为了测量出A ， B两点之间的距离，在地面上找到一点C，连接BC ， AC ， 使∠ACB=90°，然后在BC的延长线上确定D ， 使CD＝BC ， 那么只要测量出AD的长度也就得到了A，B两点之间的距离，这样测量的依据是（ ）
A、AAS B、SAS C、ASA D、SSS9. 如图，在△ABC中，∠CAB＝90°，AD是高，CF是中线，BE是角平分线，BE交AD于点G，交CF于H ， 下列说法正确的是（ ）①∠AEG＝∠AGE；②BH＝CH；③∠EAG＝2∠EBC；④S△ACF＝S△BCF ．
A、①③ B、①②③ C、①③④ D、②③④10. 如图，BE是△ABC的中线，AD⊥BC交BE于点F，且BD=AE，∠EAD＝50°，则∠EBC的度数为（ ）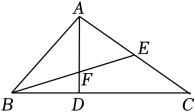
A、30° B、25° C、20° D、15°11. 如图，在△ABC和△DEF中，点B、F、C、D在同条直线上，已知∠A=∠D，AB＝DE，添加以下条件，不能判定△ABC≌△DEF的是（ ）
A、∠B＝∠E B、AC＝DF C、∠ACD＝∠BFE D、BC＝EF12. 如图，把△ABC沿EF所在直线对折，叠合后的图形如图所示．若∠A＝55°，∠1=95°则∠2的度数为（ ）
A、14° B、15° C、28° D、30°13. 如图，已知∠C＝∠D＝90°，添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等．以下给出的条件适合的是（ ）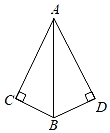
A、∠ABC＝∠ABD B、∠BAC＝∠BAD C、AC＝AD D、AC＝BC14. 如图，BD是△ABC的边AC上的中线，AE是△ABD的边BD上的中线，BF是△ABD的边AE上的中线，若△ABC的面积是32，则阴影部分的面积是（ ）
A、9 B、12 C、18 D、2015. 一块三角形玻璃被小红碰碎成四块，如图，小红只带其中的两块去玻璃店，买了一块和以前一样的玻璃 ， 你认为她带哪两块去玻璃店了（ ）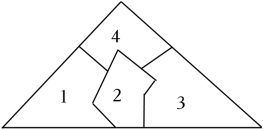
A、带其中的任意两块 B、带1，4或3，4就可以了 C、带1，4或2，4就可以了 D、带1，4或2，4或3，4均可16. 现已知线段a，b（a＜b），∠MON＝90°，求作Rt△ABO，使得∠O=90°，OA＝a，AB＝b．小惠和小雷的作法分别如下：小惠：①以点O为圆心、线段a的长为半径画弧，交射线ON于点A；②以点A为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求．
小雷：①以点O为圆心、线段a的长为半径画弧，交射线ON于点A；②以点O为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求．
则下列说法中正确的是（ ）
A、小惠的作法正确，小雷的作法错误 B、小雷的作法正确，小惠的作法错误 C、两人的作法都正确 D、两人的作法都错误二、填空题（本大题有3个小题，每小题有2个空，每空2分，共12分）
-
17. 如图，△ABC≌△BAD ， AC＝BD，则图中的对应边为 ， 对应角 ．
18. 如图，在正六边形ABCDEF的内部作正五边形DEMGH ．
∠CDH＝°；
连接EG并延长，交AB于点N ， 则∠ANE＝°．
19. 在锐角△ABC中，∠BAC＝50°，将∠α的顶点P放置在BC边上，使∠α的两边分别与边AB，AC交于点E，F（点E不与点B重合，点F不与点C重合）．设∠BEP＝x，∠CEP＝x，若∠α=40°。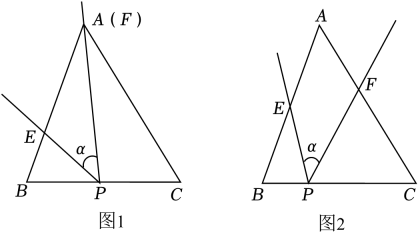
①如图1，当点F与点A重合，x＝60°时，y=°．
②如图2，当点E，F均不与点A重合时，x+y=°．
三、解答题（本大题共7个小题，共66分．解答应写出文字说明、证明过程或演算步骤）
-
20. 在△ABC中，BC＝8，AB＝1．(1)、若AC是整数，求AC的长；(2)、已知BD是△ABC的中线，若△ABD的周长为17，求△BCD的周长．21. 如图，在6×10的网格中，每一小格均为正方形且边长是1，已知△ABC的每个顶点都在格点上。
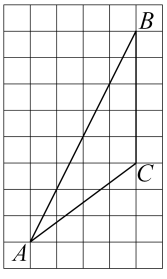(1)、画出△ABC中BC边上的高线AE；(2)、在△ABC中AB边上取点D ， 连接CD ， 使S△BCD＝3S△ACD；(3)、直接写出△BCD的面积是 ．22. 如图所示，A，D，E三点在同一直线上，且△BAD≌△ACE．
(1)、你能说明BD、DE、CE之间的数量关系吗？(2)、请你猜想△ABD满足什么条件时，BD∥CE？23. 如图，在直角三角形ABC中，∠BAC＝90°，AD是BC边上的高，CE是AB边上的中线，AB＝12cm，BC＝20cm，AC＝16cm，求：
(1)、AD的长；(2)、△BCE的面积．24. 已知：a、b、c满足 ， 求：(1)、a、b、c的值；(2)、试问以a、b、c为边能否构成三角形？若能构成三角形，求出三角形的周长；若不能构成三角形，请说明理由。
