【每日15min】33相似多边形—浙教版数学九(上)微专题精炼
试卷更新日期:2023-10-29 类型:复习试卷
一、选择题
-
1. 已知四边形ABCD∽四边形EFGH,且AB=3,EF=4,FG=5.则四边形EFGH与四边形ABCD的相似比为( )A、3:4 B、3:5 C、4:3 D、5:32. 如图,矩形ABCD∽矩形EFGH,已知 , , , 则FG的长为( )
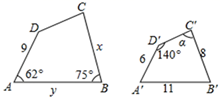
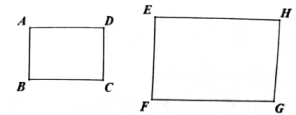 A、8cm B、10cm C、12cm D、15cm3. 如图,四边形ABCD∽四边形EFGH,∠E=85°,∠G=90°,∠D=120°,则∠B等于( )
A、8cm B、10cm C、12cm D、15cm3. 如图,四边形ABCD∽四边形EFGH,∠E=85°,∠G=90°,∠D=120°,则∠B等于( )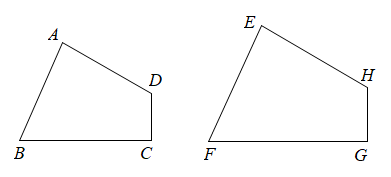 A、55° B、65° C、75° D、85°4. 矩形相邻的两边长分别为25和 , 把它按如图所示的方式分割成五个全等的小矩形,每一个小矩形均与原矩形相似,则的值为( )
A、55° B、65° C、75° D、85°4. 矩形相邻的两边长分别为25和 , 把它按如图所示的方式分割成五个全等的小矩形,每一个小矩形均与原矩形相似,则的值为( )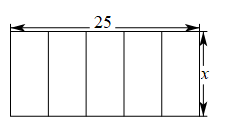 A、5 B、 C、 D、105. 两相似多边形的面积比是 , 较小多边形的周长为 , 则较大多边形的周长为( )A、 B、 C、 D、6. 一个四边形的各边之比为1∶2∶3∶4,和它相似的另一个四边形的最小边长为 , 则它的最大边长为( )A、 B、 C、 D、7. 下列与相似有关的命题中,正确的是( )
A、5 B、 C、 D、105. 两相似多边形的面积比是 , 较小多边形的周长为 , 则较大多边形的周长为( )A、 B、 C、 D、6. 一个四边形的各边之比为1∶2∶3∶4,和它相似的另一个四边形的最小边长为 , 则它的最大边长为( )A、 B、 C、 D、7. 下列与相似有关的命题中,正确的是( )①所有的等腰三角形都相似;②所有的矩形都相似;③所有的正六边形都相似.
A、①②③ B、① C、② D、③8. 如图,在平行四边形中,点分别在边上, , 四边形四边形 , 相似比 , 则下列一定能求出面积的条件( ) A、四边形和四边形的面积之差 B、四边形和四边形的面积之差 C、四边形和四边形的面积之差 D、四边形和四边形的面积之差9. 一个大矩形按如图方式分割成五个小矩形后仍是中心对称图形,且矩形矩形.设矩形与矩形的面积分别为m和n,则这个大矩形的面积一定可以表示为( )
A、四边形和四边形的面积之差 B、四边形和四边形的面积之差 C、四边形和四边形的面积之差 D、四边形和四边形的面积之差9. 一个大矩形按如图方式分割成五个小矩形后仍是中心对称图形,且矩形矩形.设矩形与矩形的面积分别为m和n,则这个大矩形的面积一定可以表示为( )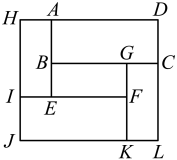 A、 B、 C、 D、10. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )
A、 B、 C、 D、10. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )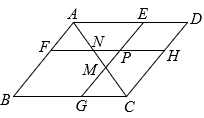 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若两个相似多边形的相似比是2:3,则它们的周长比是 .12. 制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是元.13. 四边形ABCD和四边形A'B'C'D'是相似图形,点A,B,C,D分别与点A',B',C',D'对应,已知BC=3,CD=2.4,B'C'=2,那么C'D'的长是.14. 如图,在菱形中, , 点E、F是对角线上的点(点E、F不与B、D重合),分别连接若四边形是菱形,且与菱形是相似菱形,那么菱形的边长是 . (用a的代数式表示).
 15. 如图,把矩形Ⅰ、一个小正方形和由大小相同的四个正方形组成的 L 型放入矩形 ABCD 中.矩形Ⅰ的一个顶点落在 L 型中正方形的顶点 E 处,其他顶点在矩形 ABCD 的边上; L 型中的正方形有三个顶点恰好在矩形 ABCD 的边上,另有一个顶点和小正方形顶点合.若矩形Ⅰ与矩形 ABCD相似,则 AB:BC 的值为.
15. 如图,把矩形Ⅰ、一个小正方形和由大小相同的四个正方形组成的 L 型放入矩形 ABCD 中.矩形Ⅰ的一个顶点落在 L 型中正方形的顶点 E 处,其他顶点在矩形 ABCD 的边上; L 型中的正方形有三个顶点恰好在矩形 ABCD 的边上,另有一个顶点和小正方形顶点合.若矩形Ⅰ与矩形 ABCD相似,则 AB:BC 的值为.
三、综合题