【每日15min】32相似三角形的应用—浙教版数学九(上)微专题精炼
试卷更新日期:2023-10-29 类型:复习试卷
一、选择题
-
1. 如图,它是物理学中小孔成像的原理示意图,已知物体 , 根据图中尺寸 , 则的长应是( )
 A、15 B、30 C、20 D、102. 如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点 , 镜子 , 树底三点在同一水平线上,眼睛与地面的高度为1.6米,米,米,则树高为( )米
A、15 B、30 C、20 D、102. 如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点 , 镜子 , 树底三点在同一水平线上,眼睛与地面的高度为1.6米,米,米,则树高为( )米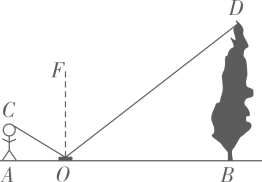 A、4 B、5 C、6 D、73. 如图,利用标杆BE测量建筑物的高度,已知标杆高 , 测得.则建筑物的高是( )
A、4 B、5 C、6 D、73. 如图,利用标杆BE测量建筑物的高度,已知标杆高 , 测得.则建筑物的高是( ) A、 B、 C、 D、4. “跳眼法”是炮兵常用的一种简易测距方法,如图,点A为左眼,点B为右眼,点O为右手大拇指,点C为敌人的位置,点D为敌人正左侧方的某一个参照物 , 已知大多数人的眼距长约为6.4厘米左右,而手臂长约为64厘米左右.若的估测长度为50米,那么的大致距离为( )米.
A、 B、 C、 D、4. “跳眼法”是炮兵常用的一种简易测距方法,如图,点A为左眼,点B为右眼,点O为右手大拇指,点C为敌人的位置,点D为敌人正左侧方的某一个参照物 , 已知大多数人的眼距长约为6.4厘米左右,而手臂长约为64厘米左右.若的估测长度为50米,那么的大致距离为( )米.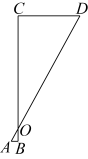 A、250 B、320 C、500 D、7505. 如图,广场上有一盏路灯挂在高的电线杆顶上,记电线杆的底部为 . 把路灯看成一个点光源,一名身高的女孩站在点处, , 则女孩的影子长为( )
A、250 B、320 C、500 D、7505. 如图,广场上有一盏路灯挂在高的电线杆顶上,记电线杆的底部为 . 把路灯看成一个点光源,一名身高的女孩站在点处, , 则女孩的影子长为( ) A、 B、 C、 D、6. 如图,测量小玻璃管口径的量具ABC,AB的长为3cm,AC被分为6等份.若小玻璃管口DE正好对着量具上2等份处(DE∥AB),那么小玻璃管口径DE的长为( )
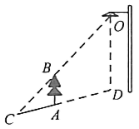
A、 B、 C、 D、6. 如图,测量小玻璃管口径的量具ABC,AB的长为3cm,AC被分为6等份.若小玻璃管口DE正好对着量具上2等份处(DE∥AB),那么小玻璃管口径DE的长为( ) A、1cm B、cm C、2cm D、cm7. 如图所示为我市某农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏脚着地时捣头点E距离地面0.8米 ,则捣头点E着地时,踏脚点D距离地面( )
A、1cm B、cm C、2cm D、cm7. 如图所示为我市某农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏脚着地时捣头点E距离地面0.8米 ,则捣头点E着地时,踏脚点D距离地面( )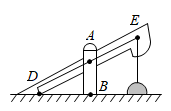 A、0.4 米 B、0.48米 C、0.5 米 D、0.8米8. 大约在两千五百年前,如图1墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是9cm,则蜡烛火焰的高度是( )
A、0.4 米 B、0.48米 C、0.5 米 D、0.8米8. 大约在两千五百年前,如图1墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是9cm,则蜡烛火焰的高度是( )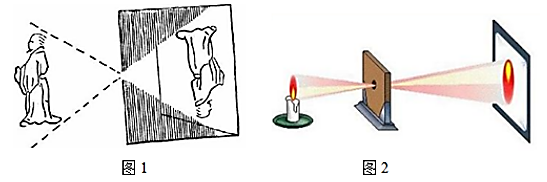 A、6cm B、8cm C、10cm D、12cm
A、6cm B、8cm C、10cm D、12cm二、填空题
-
9. 如图,树在路灯O的照射下形成投影 , 已知路灯高 , 树影 , 树与路灯O的水平距离 , 则树的高度长是.
 10. 如图1是液体沙漏的立体图形,图2,图3分别是液体沙漏某一时刻沙漏上半部分液体长度与液面距离水平面高度的平面示意图,则图3中AB=cm.
10. 如图1是液体沙漏的立体图形,图2,图3分别是液体沙漏某一时刻沙漏上半部分液体长度与液面距离水平面高度的平面示意图,则图3中AB=cm.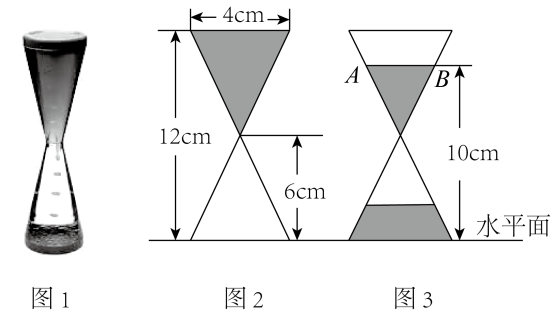 11. 如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来( , , 与相交于点O),已知米,米,米,米,则汽车从A处前行的距离米时,才能发现C处的儿童.
11. 如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来( , , 与相交于点O),已知米,米,米,米,则汽车从A处前行的距离米时,才能发现C处的儿童.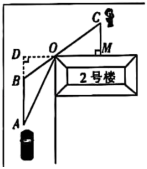 12. 如图1所示的是古代一种可以远程攻击的投石车,图2是投石车投石过程中某时刻的示意图,是杠杆,弹袋挂在点 , 重锤挂在点 , 点为支点,点是水平底板上的一点,米,米.
12. 如图1所示的是古代一种可以远程攻击的投石车,图2是投石车投石过程中某时刻的示意图,是杠杆,弹袋挂在点 , 重锤挂在点 , 点为支点,点是水平底板上的一点,米,米.
 (1)、投石车准备时,点恰好与点重合,此时和垂直,则米.(2)、投石车投石过程中,的延长线交线段于点 , 若:: , 则点距地面为米.
(1)、投石车准备时,点恰好与点重合,此时和垂直,则米.(2)、投石车投石过程中,的延长线交线段于点 , 若:: , 则点距地面为米.三、解答题
-
13. 如图,A、B两点被池塘隔开,在外任选一点C,分别在、上取点D、E,如果测得 , , , , 且 , 求的长?
 14. 雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB.
14. 雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB.
四、综合题
-
15. 如图1,长、宽均为3cm,高为8cm的长方体容器,放置在水平桌面上,里面盛有水,水面高为6cm,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,将这个情景转化成几何图形,如图3所示.
 (1)、利用图1、图2所示水的体积相等,求的长;(2)、求水面高度 .16. 学习了相似三角形相关知识后,小明和同学们想利用“标杆”测量大楼的高度.如图,小明站立在地面点F处,他的同学在点B处竖立“标杆” , 使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上(点F、B、D也在一条直线上).已知小明的身高米,“标杆”米,又米,米.
(1)、利用图1、图2所示水的体积相等,求的长;(2)、求水面高度 .16. 学习了相似三角形相关知识后,小明和同学们想利用“标杆”测量大楼的高度.如图,小明站立在地面点F处,他的同学在点B处竖立“标杆” , 使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上(点F、B、D也在一条直线上).已知小明的身高米,“标杆”米,又米,米.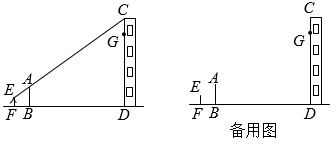 (1)、求大楼的高度为多少米(垂直地面)?(2)、小明站在原来的位置,同学们通过移动标杆,可以用同样的方法测得楼上点G的高度米,那么相对于第一次测量,标杆应该向大楼方向移动米.17. 如图为幸福小区入口处安装的汽车出入道闸示意图.如图1,道闸关闭时,四边形是矩形.如图2,在道闸打开的过程中,边固定,直线l,连杆、分别绕点A、D转动,且边始终与边平行,P为上的一点(不与点C,D重合),过点P作直线l, , 垂足分别为E,F,即四边形是矩形,过点D作 , 垂足为Q,延长与相交于点R.
(1)、求大楼的高度为多少米(垂直地面)?(2)、小明站在原来的位置,同学们通过移动标杆,可以用同样的方法测得楼上点G的高度米,那么相对于第一次测量,标杆应该向大楼方向移动米.17. 如图为幸福小区入口处安装的汽车出入道闸示意图.如图1,道闸关闭时,四边形是矩形.如图2,在道闸打开的过程中,边固定,直线l,连杆、分别绕点A、D转动,且边始终与边平行,P为上的一点(不与点C,D重合),过点P作直线l, , 垂足分别为E,F,即四边形是矩形,过点D作 , 垂足为Q,延长与相交于点R.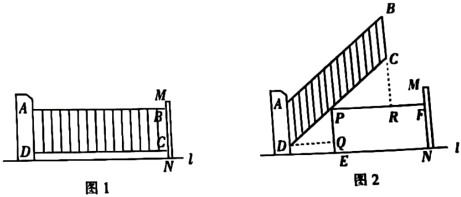 (1)、与相似吗?请判断并说明理由.(2)、若道闸长米,宽米,点D距地面米,米,米,米.
(1)、与相似吗?请判断并说明理由.(2)、若道闸长米,宽米,点D距地面米,米,米,米.①求点B到地面l的距离;
②求的长.
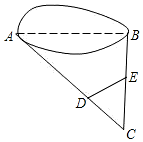
18. 学习了相似三角形知识后,小丽同学准备用自制的直角三角形纸板测量校园内一颗古树的高度.已知三角形纸板的斜边长为0.5米,较短的直角边长为0.3米.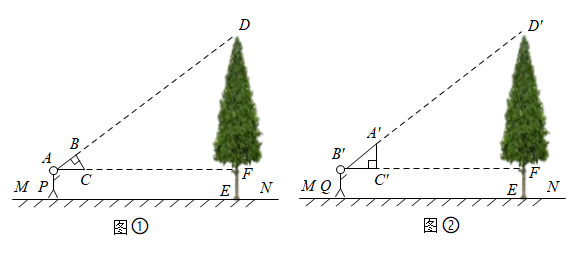 (1)、小丽先调整自己的位置至点 , 将直角三角形纸板的三个顶点位置记为、、(如图①),斜边平行于地面(点、、、在一直线上),且点在边(较长直角边)的延长线上,此时测得边距离地面的高度为1.5米,小丽与古树的距离为16米,求古树的高度;(2)、为了尝试不同的思路,小丽又向前移动自己的位置至点 , 将直角三角形纸板的三个顶点的新位置记为、、(如图②),使直角边(较短直角边)平行于地面(点、、、在一直线上),点在斜边的延长线上,且测得此时边距离地面的高度依然是1.5米,那么小丽向前移动了多少米?
(1)、小丽先调整自己的位置至点 , 将直角三角形纸板的三个顶点位置记为、、(如图①),斜边平行于地面(点、、、在一直线上),且点在边(较长直角边)的延长线上,此时测得边距离地面的高度为1.5米,小丽与古树的距离为16米,求古树的高度;(2)、为了尝试不同的思路,小丽又向前移动自己的位置至点 , 将直角三角形纸板的三个顶点的新位置记为、、(如图②),使直角边(较短直角边)平行于地面(点、、、在一直线上),点在斜边的延长线上,且测得此时边距离地面的高度依然是1.5米,那么小丽向前移动了多少米?