【每日15min】30相似三角形的性质—浙教版数学九（上）微专题精炼

试卷更新日期：2023-10-29 类型：复习试卷

进入出卷网下载

一、选择题

1. 两个相似三角形的相似比是4：9，则它们的面积比是（）

A、4：9 B、16：81 C、2：3 D、1：3

查看试题解析
2. 已知在△ABC中，AB=6，AC=9，D，E分别是AB，AC边上的点，且AD=2. 若△ABC和△ADE相似，则AE=（）

A、5 B、3 C、 $\frac{4}{3}$ D、3或 $\frac{4}{3}$

查看试题解析
3. 已知△ABC∽△DEF，AB：DE＝3：1，AC＝6，则DF为（　　）

A、18 B、2 C、54 D、 $\frac{2}{3}$

查看试题解析
4. 如图所示， $△ A B D ∽ △ A C B$ ， $A D = 1$ ， $A B = 2$ ，则 $A C$ 的长为（）

A、 $\sqrt{2}$ B、2 C、3 D、4

查看试题解析
5. 如图，在直角梯形 $A B C D$ 中， $∠ A B C = 90 °$ ， $A B = 8$ ， $A D = 3$ ， $B C = 4$ ，点 $P$ 为边 $A B$ 上一动点，若 $△ P A D$ 与 $△ P B C$ 是相似三角形，则满足条件的点 $P$ 的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图， $△ A B C$ 内接于 $⊙ O$ ，且 $A C = B C$ ， $A O$ 的延长线交 $B C$ 于点 $E$ ，若 $△ A B E$ 与 $△ A B C$ 相似，则 $∠ A B C =$ （）.

A、 $55 °$ B、 $65 °$ C、 $67.5 °$ D、 $72 °$

查看试题解析
7. 如图，Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，下列结论中错误的是（）

A、AC²＝AD•AB B、BC²＝BD•BA C、CD²＝AD•DB D、CD²＝CA•CB

查看试题解析
8. 如图，在 $A B C$ 纸板中， $A C = 4$ ， $B C = 8$ ， $A B = 11$ ， $P$ 是 $B C$ 上一点，沿过点 $P$ 的直线剪下一个与 $△ A B C$ 相似的小三角形纸板．针对 $C P$ 的不同取值，三人的说法如下．下列判断正确的是（）

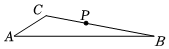
甲：若 $C P = 4$ ，则有 $3$ 种不同的剪法；

乙：若 $C P = 2$ ，则有 $4$ 种不同的剪法；

丙：若 $C P = 1$ ，则有 $3$ 种不同的剪法．

A、乙错，丙对 B、甲和乙都错 C、乙对，丙错 D、甲错，丙对

查看试题解析

二、填空题

9. 如图，正方形 $A B C D$ 的边长为6，点F为 $A B$ 的中点，点E在 $A D$ 上，且 $E D = 2 A E$ ，在边 $C D$ 上找一点P，使以E，D，P为顶点的三角形与 $△ A E F$ 相似，则 $D P$ 的长为.

查看试题解析
10. 如图，点 $D$ 在等边三角形 $A B C$ 的边 $B C$ 上，连接 $A D$ ，线段 $A D$ 的垂直平分线 $E F$ 分别交边 $A B$ ， $A C$ 于点 $E$ ， $F .$ 当 $2 C D = 3 B D$ 时， $\frac{A E}{A F}$ 的值为．

查看试题解析
11. 若△ABC∽△A'B'C'，且 $\frac{A B}{A' B'} = \frac{3}{4}$ ， △ABC的周长为12 cm，则△A'B'C'的周长为cm．

查看试题解析
12. 如图，点D是△ABC的重心，延长AD交BC于点O，△DEF是由△ABC经过位似变化得到的，点O是位似中心，则△DEF与△ABC的面积比是．

查看试题解析
13. 已知过点 $B (3 ， - 1)$ 的抛物线 $y = \frac{1}{2} x^{2} - \frac{5}{2} x + c$ 与坐标轴交于点 $A$ 、 $C$ 如图所示，连结 $A C$ ， $B C$ ， $A B$ ，第一象限内有一动点 $M$ 在抛物线上运动，过点 $M$ 作 $A M ⊥ M P$ 交 $y$ 轴于点 $P$ ，当点 $P$ 在点 $A$ 上方，且 $△ A M P$ 与 $△ A B C$ 相似时，点 $M$ 的坐标为.

查看试题解析

三、作图题

14. 如图，在直角坐标系中， $△$ ABC各顶点的坐标为 $A (- 1 ， 1)$ ， B（2，3），C（0，3）.

(1)、以坐标原点O为位似中心，在x轴上方作与 $△$ ABC的位似比为2的位似图形 $△ A^{'} B^{'} C^{'}$ .

(2)、顶点 $A^{'}$ 的坐标为， $△ A^{'} B^{'} C^{'}$ 与 $△$ ABC的面积之比为.

查看试题解析
15. 如图，在 $7 \times 7$ 的方格中，点A、B、C均在格点上.（要求：①只用无刻度的直尺按要求作图，各画出一条即可；②所作的点P，点Q均在格点上；③先用铅笔画，再用签字笔描黑.）　

(1)、在图1作 $P Q$ 平分 $A B$ ；

(2)、在图2作 $P Q$ 垂直平分 $A B$ ；

(3)、在图3中作 $P Q$ ， $P Q$ 与线段 $A B$ 的交点为D，使 $B D = \frac{3}{2} A D$ .

查看试题解析

四、解答题

16. 如图，在矩形 $A B C D$ 中，点E，F分别在边 $A D$ ， $D C$ 上， $△ A B E ∽ △ D E F$ ， $D F > D E$ ， $A B = 9$ ， $A E = 12$ ， $D E = 3$ ，求 $F C$ 的长.

查看试题解析
17. 如图，在平面直角坐标系中，四边形OABC是正方形，点B坐标为（2 $\sqrt{2}$ ， 0），点D是射线OB上不与点O重合的一个动点，将线段CD绕点D顺时针旋转90°得到ED，连结AD、AE.

(1)、求证：DA＝DE；

(2)、如图2，连结AC，BE，当△CDA与△DBE相似时，求BD的长；

(3)、当点A关于直线ED的对称点A'落在正方形的边上时，求点D的坐标.

查看试题解析
18. 已知菱形 $O A B C$ 的边长为5，且点 $A (3 ， 4)$ ，点E是线段 $B C$ 的中点，过点A，E的抛物线 $y = a x^{2} + b x + c$ 与边 $A B$ 交于点D，

(1)、求点E的坐标；

(2)、连接DE，将△BDE沿着DE翻折.
①当 $点 B$ 的对应点 $B^{'}$ 恰好落在线段 $A C$ 上时，求点D的坐标；

②连接 $O B$ ， $B B^{'}$ ，若 $△ B B^{'} D$ 与 $△ B O C$ 相似，请直接写出此时抛物线二次项系数 $a =$ .

查看试题解析