北师大版数学九（上）期中题型汇编15 探究性试题-在线组卷题库

1. 阅读材料：设一元二次方程ax²+bx+c＝0(a≠0)的两根为x₁ ， x₂ ，则两根与方程系数之间有如下关系：

x_{1} + x_{2} = - \frac{b}{a}

，x₁·x₂＝

\frac{c}{a}

．根据该材料解题：已知x₁ ， x₂是方程x²−2x=1的两实数根．

求：

(1)、

x_{1}^{2} + x_{2}^{2}

(2)、

\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}}

查看试题解析

2. 阅读材料，并回答问题：

下面是小明解方程 $x^{2} + 4 x - 2 = 0$ 的过程：

解：移项，得

$x^{2} + 4 x = 2$ ． ①

配方，得

$x^{2} + 4 x + 4 = 2$ ， ②

$(x + 2)^{2} = 2$ ． ③

由此可得

$x + 2 = \pm \sqrt{2}$ ， ④

$x_{1} = \sqrt{2} - 2$ ， $x_{2} = - \sqrt{2} - 2$ ． ⑤

(1)、小明解方程的方法是____；

A、直接开平方法 B、配方法 C、公式法 D、因式分解法

(2)、上述解答过程中，从第步（填序号）开始出现了错误，原因是；

(3)、请你写出正确的解答过程．

查看试题解析

3. 下面是小明解决某数学问题的过程，请认真阅读并解决相应学习任务：

数学问题：某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：（）．现已知商品的进价为每件40元，如何定价才能使每个星期的利润达到6080元，且顾客能够得到更大的实惠？

解：设…，

根据题意，所列出方程：（20﹣x）（300＋ $\frac{x}{2}$ ×40）＝6080，

…

根据小明所列方程，完成下列任务：

(1)、填空：数学问题中括号处短缺的条件是，小明所列方程中未知数x的实际意义是．

(2)、请你重新设一个未知数，要求所设未知数与小明所列方程中未知数的意义不同，并结合所补充的条件，解决上面的数学问题．

查看试题解析

4. 阅读材料：各类方程的解法不尽相同，但是它们有一个共同的基本数学思想——转化，把未知转化为已知.用“转化”的数学思想，我们还可以解一些新的方程.例如，一元三次方程

x^{3} - 2 x^{2} - 3 x = 0

，通过因式分解可以把它转化为

x (x^{2} - 2 x - 3) = 0

，解方程

x = 0

和

x^{2} - 2 x - 3 = 0

，可得方程

x^{3} - 2 x^{2} - 3 x = 0

的解.

问题：

(1)、方程

x^{3} - 2 x^{2} - 3 x = 0

的解是

x_{1} = 0

，

x_{2} =

，

x_{3} =

.

(2)、求方程

x^{3} = 6 x^{2} + 16 x

的解.

(3)、拓展：

用“转化”思想求方程 $\sqrt{- 2 x + 15} = x$ 的解.

查看试题解析

5. 探究：如图①，直线l₁∥l₂∥l₃ ，点C在l₂上，以点C为直角顶点作∠ACB＝90°，角的两边分别交l₁与l₃于点A、B，连结AB，过点C作CD⊥l₁于点D，延长DC交l₃于点E．

(1)、求证：△ACD∽△CBE．

(2)、应用：如图②，在图①的基础上，设AB与l₂的交点为F，若AC＝BC，l₁与l₂之间的距离为2，l₂与l₃之间的距离为1，则AF的长度是　　．

查看试题解析

6. 综合与实践

问题情境：如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，将 $△ A B C$ 绕点B顺时针旋转得到 $R t △ E B D$ ，连接 $A E$ ，连接 $C D$ 并延长交 $A E$ 于点F．

(1)、猜想验证：

试猜想 $△ C B D$ 与 $△ A B E$ 是否相似？并证明你的猜想．

(2)、探究证明：

如图，连接 $B F$ 交 $D E$ 于点H， $A B$ 与 $C F$ 相交于点G， $\frac{D H}{B H} = \frac{F H}{E H}$ 是否成立？并说明理由．

(3)、拓展延伸：

若 $C D = E F$ ，直接写出 $\frac{B C}{A B}$ 的值．

查看试题解析

7. 数学思想方法作为数学学科的一般原理，在数学学习中至关重要．我们经常运用类比，转化，从特殊到一般等思想方法来解决一些数学问题．

如图①，在平行四边形 $A B C D$ 中，点E是 $B C$ 边的中点，点F是线段 $A E$ 上一点， $B F$ 的延长线交 $C D$ 于点 $G$ ．若 $\frac{A F}{E F} = 5$ ，求 $\frac{C D}{C G}$ 的值．

(1)、【尝试探究】

在图①中，过点E作 $E H ∥ A B$ 交 $B G$ 于点 $H$ ，则 $\frac{A B}{E H}$ 的值为， $\frac{C G}{E H}$ 的值为， $\frac{C D}{C G}$ 的值为．

(2)、【类比延伸】

如图②，在原题的条件下，若 $\frac{A F}{E F} = m$ ，则 $\frac{C D}{C G}$ 的值为（用含 $m$ 的代数式表示）．

(3)、【拓展迁移】

如图③，若点F在线段 $A E$ 的延长线上， $B F$ 的延长线交 $D C$ 的延长线于点 $G$ ， $\frac{A F}{E F} = n$ ，则 $\frac{C D}{C G}$ 的值为（用含n的代数式表示）．

查看试题解析

8.

(1)、[基础巩固]如图1，在四边形

A B C D

中，对角线

B D

平分

∠ A B C

，

∠ A D B = ∠ D C B

，求证：

B D^{2} = B A \cdot B C

；

(2)、 [尝试应用]

如图2，四边形 $A B C D$ 为平行四边形，F在 $A D$ 边上， $A B = A F$ ，点E在 $B A$ 延长线上，连接 $E F 、 B F 、 C F$ ，若 $∠ E F B = ∠ D F C$ ， $B E = 4 ， B F = 5$ ，求 $A D$ 的长；

(3)、 [拓展提高]

如图3，在 $△ A B C$ 中，D是 $B C$ 上一点，连接 $A D$ ，点E、F分别在 $A D$ 、 $A C$ 上，连接 $B E 、 C E 、 E F$ ，若 $D E = D C$ ， $∠ B E C = ∠ A E F$ ， $B E = 18 ， E F = 7$ ， $\frac{C E}{B C} = \frac{2}{3}$ ；求 $\frac{A F}{F C}$ 的值.

查看试题解析

9. 综合与实践

问题情境：如图1，四边形 $A B C D$ 和 $E F C G$ 都是正方形，点G，F分别在边 $C D$ 和 $C B$ 上，点E在正方形 $A B C D$ 的内部．

(1)、猜想证明：

$D G$ 和 $B F$ 的位置关系是， $D G$ 和 $B F$ 的数量关系是．

(2)、将正方形

E F C G

以C为中心顺时针方向旋转到图2所示位置，则（1）中的结论是否仍然成立？请说明理由．

(3)、如图3，在正方形

E F C G

以C为中心顺时针旋转的过程中，当点E落在正方形

A B C D

的边

A D

上时，若

C B = 17

，

C F = 13

，则

B F

的长度是．（请直接写出答案即可）

查看试题解析

10. 请阅读以下材料，并完成相应的问题：

角平分线分线段成比例定理，如图1，在△ABC中，AD平分∠BAC，则 $\frac{A B}{A C} = \frac{B D}{C D}$ ．

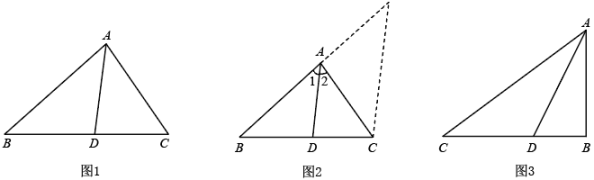
下面是这个定理的部分证明过程．

证明：如图2，过点C作 $C E ∥ D A$ ．交BA的延长线于点E．…

任务：

(1)、请按照上面的证明思路，写出该证明过程的剩余部分；

(2)、如图3，已知Rt△ABC中，AB＝3，BC＝4，∠ABC＝90°，AD平分∠BAC，求△ABD的周长．

查看试题解析

11. 解答题

(1)、如图1，

△ A B C

和

△ A D E

都是等边三角形，连接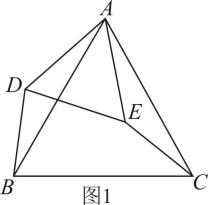

B D

、

C E

，求证，

B D = C E

；

(2)、[类比探究]

如图2， $△ A B C$ 和 $△ A D E$ 都是等腰直角三角形， $∠ A B C = ∠ A D E = 90 °$ ，连接 $B D ， C E$ ．求 $\frac{B D}{C E}$ 的值．

(3)、[拓展提升]

如图3， $△ A B C$ 和 $△ A D E$ 都是直角三角形， $∠ A B C = ∠ A D E = 90 °$ ， $\frac{A C}{A B} = \frac{A E}{A D} = 2$ ．连接 $B D 、 C E$ ，延长 $C E$ 交 $B D$ 于点F，连接 $A F$ ．若 $∠ A F C$ 恰好等于 $90 °$ ，请直接写出此时 $A F ， B F ， C F$ 之间的数量关系．

查看试题解析

12. 如图，正方形ABCD的四个顶点分别在正方形EFGH的四条边上，我们称正方形EFGH是正方形ABCD的外接正方形．

探究一：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍？如图，假设存在正方形EFGH，它的面积是正方形ABCD的2倍．

因为正方形ABCD的面积为1，则正方形EFGH的面积为2，

所以EF＝FG＝GH＝HE＝ $\sqrt{2}$ ，设EB＝x，则BF＝ $\sqrt{2}$ ﹣x，

∵Rt△AEB≌Rt△BFC

∴BF＝AE＝ $\sqrt{2}$ ﹣x

在Rt△AEB中，由勾股定理，得

x²+（ $\sqrt{2}$ ﹣x）²＝1²

解得，x₁＝x₂＝ $\frac{\sqrt{2}}{2}$

∴BE＝BF，即点B是EF的中点．

同理，点C，D，A分别是FG，GH，HE的中点．

所以，存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍

探究二：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的3倍？（仿照上述方法，完成探究过程）

探究三：已知边长为1的正方形ABCD， ▲ 一个外接正方形EFGH，它的面积是正方形ABCD面积的4倍？（填“存在”或“不存在”）

探究四：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的n倍？（n＞2）（仿照上述方法，完成探究过程）

查看试题解析

13. 请阅读以下材料，并完成相应的问题：

角平分线分线段成比例定理，如图1，在△ABC中，AD平分∠BAC，则 $\frac{A B}{A C} = \frac{B D}{C D}$ ．

下面是这个定理的部分证明过程．

证明：如图2，过点C作 $C E ∥ D A$ ．交BA的延长线于点E．…

(1)、任务：

请按照上面的证明思路，写出该证明过程的剩余部分；

(2)、如图3，已知Rt△ABC中，AB＝3，BC＝4，∠ABC＝90°，AD平分∠BAC，求△ABD的周长．

查看试题解析

14. 【了解概念】

在凸四边形中，若一边与它的两条邻边组成的两个内角相等，则称该四边形为邻等四边形，这条边叫做这个四边形的邻等边.

(1)、【理解运用】
邻等四边形ABCD中，∠A=30°，∠B=70°，则∠C的度数为 .

(2)、如图，凸四边形ABCD中，P为AB边的中点，△ADP∽△PDC，判断四边形ABCD是否为邻等四边形；并证明你的结论；

(3)、【拓展提升】
在平面直角坐标系中，AB为邻等四边形ABCD的邻等边，且AB边与x轴重合，已知A（-1，0），C（m，2

\sqrt{3}

），D（2，3

\sqrt{3}

），若在边AB上使∠DPC=∠BAD的点P有且仅有1个，请直接写出m的值．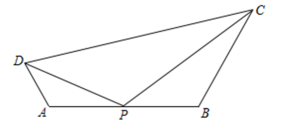

查看试题解析

15. 【问题提出】已知有两个Rt△ABC和Rt△A'B′C'，其中∠C＝∠C′＝90°，∠A＝60°，∠A′＝45°．

(1)、如图1，作线段CD，C′D′，分别交AB于点D，交A'B′于点D′，使得∠BCD＝45°，∠B'C′D'＝30°，问△BCD与△B'C′D'，△ACD与△A′C′D′是否相似？并选择其中相似的一对三角形，说明理由．

(2)、如图2，作线段AD，B'D′，分别交BC于点D，交A'C'于点D，若△ACD与△B′C′D′、△ABD与△A′B'D'均相似，求∠CAD，∠C'B'D′的度数．

(3)、【拓展思考】已知任意两个不相似的直角三角形，能否分别作一条直线对其进行分割，使其中一个三角形所分割得到的两个三角形与另一个三角形所分割得到的两个三角形分别对应相似？如果可以，请直接画出一种分割示意图；如果不能，请说明理由．

查看试题解析

16.

(1)、[证明体验]

如图13-1，AD为△ABC的角平分线，∠ADC=60°，点E在AB上，AE=AC．求证：DE平分∠ADB．

(2)、[思考探究]

如图13-2，在(1)的条件下，F为AB上一点，连结FC交AD于点G．若FB=FC，DG=2，CD=3，求BD的长．

(3)、[拓展延伸]

如图13-3，在四边形ABCD中，对角线AC平分∠BAD，∠BCA=2∠DCA，点E在AC上，∠EDC=∠ABC．若BC=5，CD=2 $\sqrt{5}$ ，AD=2AE，求AC的长．

查看试题解析

17. （问题提出）：

(1)、如图1，在Rt△ABC中，∠ACB＝90°，AC＞BC ， ∠ACB的平分线交AB于点P ，过点P分别作PE⊥AC ， PF⊥BC ，垂足分别为E ， F ，则图1中四边形PECF的形状为 .请写出证明过程．

(2)、（问题探究）：

如图2，在Rt△ABC中，∠ACB＝90°，AB＝10cm ， AC＝8cm ， ∠ACB的平分线交AB于点P ，过点P分别作PE⊥AC ， PF⊥BC ，垂足分别为E ， F ，求四边形PECF的面积．请写出解答过程．

查看试题解析

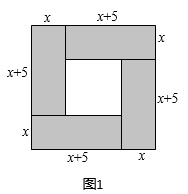
18. 请阅读下列材料，并按要求完成相应的任务：

人类对一元二次方程的研究经历了漫长的岁月．一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中．到了中世纪，阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法，并用几何法进行了证明．我国古代三国时期的数学家赵爽也给出了类似的几何解法．赵爽在其所著的《勾股圆方图注》中记载了解方程 $x^{2} + 5 x -14 = 0$ 即 $x (x + 5) = 14$ 得方法.首先构造了如图1所示得图形，图中的大正方形面积是 ${(x + x + 5)}^{2}$ ，其中四个全等的小矩形面积分别为 $x (x + 5) = 14$ ，中间的小正方形面积为 $5^{2}$ ，所以大正方形的面积又可表示为 $4 \times 14 + 5^{2}$ ，据此易得 $x = 2$ ．

任务：

(1)、参照上述图解一元二次方程的方法，请在下面三个构图中选择能够说明方程

x^{2} -4 x -12 = 0

的正确构图是（从序号①②③中选择）．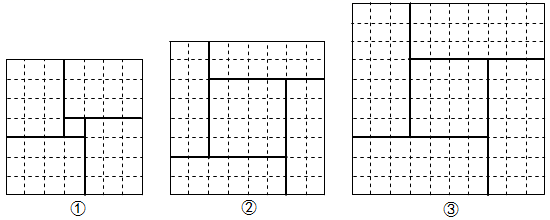

(2)、请你通过上述问题的学习，在图2的网格中设计正确的构图，用几何法求解方程

x^{2} + 2 x -15 = 0

（写出必要的思考过程）．

查看试题解析

19. 阅读与思考

请阅读下列材料，并完成相应的任务：

阿尔·花拉子米(约780~约850) ，著名阿拉伯数学家、天文学家、地理学家，是代数与算术的整理者，被誉为“代数之父”。他利用正方形图形巧妙解出了一元二次方程x²+2x-35=0的一个解．将边长为x的正方形和边长为1的正方形，外加两个长方形，长为x，宽为1，拼合在一起面积就是x²+2·x×1+1² ，即x²+2x+ 1，而由原方程x²+2x-35=0变形得x²+2x+1=35+1，即边长为x+1的正方形面积为36．所以(x+1)²=36，则x=5．

任务：

(1)、上述求解过程中所用的方法与下列哪种方法是一致的（）

A、直接开平方法 B、公式法 C、配方法 D、因式分解法

(2)、所用的数学思想方法是（）

A、分类讨论思想 B、数形结合思想 C、建模思想 D、整体思想

(3)、运用上述方法构造出符合方程x²+6x-7=0的一个正根的正方形(画出拼接的正方形并求出正根)．

查看试题解析

20. 综合与实践：

问题情境：在一次综合实践活动课上，同学们以菱形为对象，研究菱形旋转中的问题：

已知，在菱形ABCD中，BD为对角线， $∠ B A D = 60^{\circ}$ ，AB=4，将菱形ABCD绕顶点A顺时针旋转，旋转角为 $α$ （单位°）．旋转后的菱形为 $A B^{'} C^{'} D^{'}$ ．在旋转探究活动中提出下列问题，请你帮他们解决．

(1)、观察证明：
如图1，若旋转角

α < 60^{\circ}

，

A D^{'}

与BD相交于点M，AB与

B^{'} D^{'}

相交于点N．请说明线段DM与

B^{'} N

的数量关系；

(2)、操作计算：
如图2，连接

C D^{'}

，菱形ABCD旋转的过程中，当

B^{'} D^{'}

与AB互相垂直时，

C D^{'}

的长为；

(3)、如图3，若旋转角

α < 60^{\circ}

，分别连接

D D^{'}

，

B D^{'}

，过点A分别作

A E ⊥ D D^{'}

，

A F ⊥ B D^{'}

，连接EF，菱形ABCD旋转的过程中，发现在

Δ A E F

中存在长度不变的线段EF，请求出EF长度；

(4)、操作探究：
如图4，在（3）的条件下，请判断以

D D^{'}

，

C D^{'}

，

B D^{'}

三条线段长度为边的三角形是什么特殊三角形，并说明理由．

查看试题解析

21. 如图

（问题情境）

如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．

（探究展示）

(1)、请你判断AM，AD，MC三条线段的数量关系，并说明理由；

(2)、AM = DE + BM是否成立？若成立，请给出证明；若不成立，请说明理由．

(3)、若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否仍然成立？请分别作出判断，不需要证明．

查看试题解析

22. 请你认真阅读下面的小探究系列，完成所提出的问题．

(1)、如图（1），将角尺放在正方形

A B C D

上，使角尺的直角顶点

E

与正方形

A B C D

的顶点

D

重合，角尺的一边交

C B

于点

F

，另一边交

B A

的延长线于点

G

．求证：

E F = E G

．

(2)、如图（2），移动角尺，使角尺的顶点

E

始终在正方形

A B C D

的对角线

B D

上，其余条件不变，请你思考后直接回答

E F

和

E G

的数量关系：

E F

E G

（用“＝”或“≠”填空）．

(3)、运用（1）、（2）解答中所积累的活动经验和数学知识，完成下题：如图（3），将（2）中的“正方形

A B C D

”改成“矩形

A B C D

”，使角尺的一边经过点

A

（即点

G

、

A

重合），其余条件不变，若

A B = 4

，

B C = 3

，求

\frac{E F}{E G}

的值．

查看试题解析

北师大版数学九（上）期中题型汇编15 探究性试题

一、实践探究题