北师大版数学九(上)期中题型汇编14 解答题—反比例函数
试卷更新日期:2023-10-29 类型:复习试卷
一、综合题
-
1. 已知反比例函数的图象经过点 .(1)、求的值;(2)、当且时,直接写出的取值范围.2. 如图,一次函数与反比例函数的图像交于 和;
 (1)、求一次函数及反比例函数的表达式;(2)、根据图像,直接写出关于x的不等式的解集.3. 如图,直线经过点 , 交反比例函数的图象于点 .
(1)、求一次函数及反比例函数的表达式;(2)、根据图像,直接写出关于x的不等式的解集.3. 如图,直线经过点 , 交反比例函数的图象于点 . (1)、求k的值;(2)、点D为第一象限内反比例函数图象上点B下方的一个动点,过点D作轴交线段AB于点C,连接AD,求的面积的最大值.4. 已知:a,b,c三个数满足关系式 .(1)、填空::4: .(2)、若 , 试求出的值.(3)、在(2)的基础上,若点是反比例函数的图像上的任意一点,过点向轴引垂线,垂足为 , 请直接写出的面积.5. 如图,一次函数()与反比例函数()的图象交于A , B两点.
(1)、求k的值;(2)、点D为第一象限内反比例函数图象上点B下方的一个动点,过点D作轴交线段AB于点C,连接AD,求的面积的最大值.4. 已知:a,b,c三个数满足关系式 .(1)、填空::4: .(2)、若 , 试求出的值.(3)、在(2)的基础上,若点是反比例函数的图像上的任意一点,过点向轴引垂线,垂足为 , 请直接写出的面积.5. 如图,一次函数()与反比例函数()的图象交于A , B两点.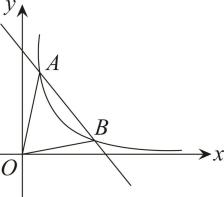 (1)、求一次函数的解析式;(2)、根据图象,直接写出使成立的的取值范围;(3)、求的面积.6. 教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降.水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)、求一次函数的解析式;(2)、根据图象,直接写出使成立的的取值范围;(3)、求的面积.6. 教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降.水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题: (1)、分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;(2)、求出图中a的值;(3)、李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40℃的开水,则他需要在什么时间段内接水?7. 如图,在平面直角坐标系中,直线与双曲线相交于两点.
(1)、分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;(2)、求出图中a的值;(3)、李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40℃的开水,则他需要在什么时间段内接水?7. 如图,在平面直角坐标系中,直线与双曲线相交于两点. (1)、求对应的函数表达式;(2)、过点B作轴交y轴于点P,求的面积;(3)、根据函数图象,直接写出关于x的不等式的解集.8. 密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:)变化时,气体的密度(单位:)随之变化.已知密度与体积V是反比例函数关系,它的图象如图所示,当时, .
(1)、求对应的函数表达式;(2)、过点B作轴交y轴于点P,求的面积;(3)、根据函数图象,直接写出关于x的不等式的解集.8. 密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:)变化时,气体的密度(单位:)随之变化.已知密度与体积V是反比例函数关系,它的图象如图所示,当时, . (1)、求密度关于体积V的函数解析式;(2)、若 , 求二氧化碳密度的变化范围.9. 如图,在中, , , 点 , 点 , 反比例函数的图象经过点A.
(1)、求密度关于体积V的函数解析式;(2)、若 , 求二氧化碳密度的变化范围.9. 如图,在中, , , 点 , 点 , 反比例函数的图象经过点A. (1)、求反比例函数的表达式;(2)、将直线向上平移m个单位后经过反比例函数图象上的点 , 求m的值.10. 如图,一次函数的图形与反比例函数的图象交于点P,点P在第一象限,轴于点A,一次函数的图象分别交x轴、y轴于点C、D,且 , .
(1)、求反比例函数的表达式;(2)、将直线向上平移m个单位后经过反比例函数图象上的点 , 求m的值.10. 如图,一次函数的图形与反比例函数的图象交于点P,点P在第一象限,轴于点A,一次函数的图象分别交x轴、y轴于点C、D,且 , .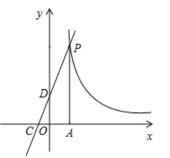 (1)、求点D的坐标;(2)、求一次函数与反比例函数的解析式;(3)、根据图象直接写出当时,一次函数值大于等于反比例函数的值时x的取值范围.11. 王叔叔计划购买一套商品房,首付30万元后,剩余部分用贷款并按“等额本金”的形式偿还,即贷款金额按月分期还款,每月所还贷款本金数相同.设王叔叔每月偿还贷款本金y万元,x个月还清,且y是x的反比例函数,其图象如图所示.
(1)、求点D的坐标;(2)、求一次函数与反比例函数的解析式;(3)、根据图象直接写出当时,一次函数值大于等于反比例函数的值时x的取值范围.11. 王叔叔计划购买一套商品房,首付30万元后,剩余部分用贷款并按“等额本金”的形式偿还,即贷款金额按月分期还款,每月所还贷款本金数相同.设王叔叔每月偿还贷款本金y万元,x个月还清,且y是x的反比例函数,其图象如图所示. (1)、求y与x的函数关系式;(2)、求王叔叔购买的商品房的总价;(3)、若王叔叔计划每月偿还贷款本金不超过2000元,则至少需要多少个月还清?12. 某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图),现已知上市30天时,当日销售量为120万件.
(1)、求y与x的函数关系式;(2)、求王叔叔购买的商品房的总价;(3)、若王叔叔计划每月偿还贷款本金不超过2000元,则至少需要多少个月还清?12. 某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图),现已知上市30天时,当日销售量为120万件. (1)、写出该商品上市以后销售量y(万件)与时间x(天数)之间的表达式;(2)、求上市至第100天(含第100天),日销售量在36万件以下(不含36万件)的天数;(3)、广告合同约定,当销售量不低于100万件,并且持续天数不少于12天时,广告设计师就可以拿到“特殊贡献奖”,那么本次广告策划,设计师能否拿到“特殊贡献奖”?13. 如图,已知在平面直角坐标系中,一次函数的图像经过点A、 , 反比例函数的图像也经过点A,且点A横坐标是2.
(1)、写出该商品上市以后销售量y(万件)与时间x(天数)之间的表达式;(2)、求上市至第100天(含第100天),日销售量在36万件以下(不含36万件)的天数;(3)、广告合同约定,当销售量不低于100万件,并且持续天数不少于12天时,广告设计师就可以拿到“特殊贡献奖”,那么本次广告策划,设计师能否拿到“特殊贡献奖”?13. 如图,已知在平面直角坐标系中,一次函数的图像经过点A、 , 反比例函数的图像也经过点A,且点A横坐标是2. (1)、求一次函数的解析式.(2)、点C是x轴正半轴上的一点,连接 , , 过点C作轴分别交反比例函数和一次函数的图像于点D、E,求点D、E的坐标.(3)、在(2)的条件下,连接 , 一次函数的图像上是否存在一点F使得和相似?若存在,请直接写出点F坐标;若不存在,请说明理由.14. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于 , 两点.
(1)、求一次函数的解析式.(2)、点C是x轴正半轴上的一点,连接 , , 过点C作轴分别交反比例函数和一次函数的图像于点D、E,求点D、E的坐标.(3)、在(2)的条件下,连接 , 一次函数的图像上是否存在一点F使得和相似?若存在,请直接写出点F坐标;若不存在,请说明理由.14. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于 , 两点. (1)、求反比例函数及一次函数表达式;(2)、若点P是直线左侧x轴上一点,若面积为1,求P点的坐标;(3)、过点A作直线 , 与第三象限的反比例函数图象交于另一点C,连接 , 当线段被y轴分成长度比为的两部分时,求的长.15. 如图,在直角坐标中,矩形的顶点O与坐标原点重合,顶点A、C分别在x轴和y轴上,点B的坐标为 , 反比例函数是的图象经过的中点D,且与交于点E,连接 .
(1)、求反比例函数及一次函数表达式;(2)、若点P是直线左侧x轴上一点,若面积为1,求P点的坐标;(3)、过点A作直线 , 与第三象限的反比例函数图象交于另一点C,连接 , 当线段被y轴分成长度比为的两部分时,求的长.15. 如图,在直角坐标中,矩形的顶点O与坐标原点重合,顶点A、C分别在x轴和y轴上,点B的坐标为 , 反比例函数是的图象经过的中点D,且与交于点E,连接 . (1)、求k的值及点E的坐标;(2)、若点F是边上一点,且 , 求直线的解析式.(3)、若点P在y轴上,且的面积与四边形的面积相等,求点P的坐标.16. 小丽家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热……,重复上述程序(如图所示),根据图中提供的信息,解答问题:
(1)、求k的值及点E的坐标;(2)、若点F是边上一点,且 , 求直线的解析式.(3)、若点P在y轴上,且的面积与四边形的面积相等,求点P的坐标.16. 小丽家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热……,重复上述程序(如图所示),根据图中提供的信息,解答问题: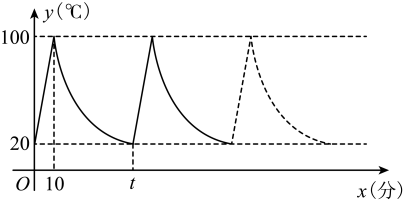 (1)、当时,求水温y(℃)与开机时间x(分)的函数关系式;(2)、求图中t的值;(3)、若小丽在通电开机后即外出散步,请你预测小丽散步70分钟回到家时,饮水机内的温度约为多少℃?17. 如图,在平面直角坐标系中,、是矩形的两个顶点,点D是线段上的一个动点(不与重合),双曲线()经过点D,与矩形的边相交于点E.
(1)、当时,求水温y(℃)与开机时间x(分)的函数关系式;(2)、求图中t的值;(3)、若小丽在通电开机后即外出散步,请你预测小丽散步70分钟回到家时,饮水机内的温度约为多少℃?17. 如图,在平面直角坐标系中,、是矩形的两个顶点,点D是线段上的一个动点(不与重合),双曲线()经过点D,与矩形的边相交于点E.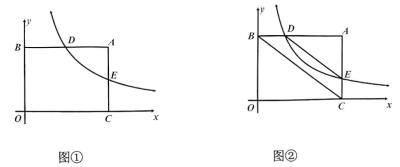
 (1)、如图①,当点D为中点时,k的值为 , 点E的坐标为;(2)、如图②,当点D在线段上的任意位置时(不与重合),连接 , 求证:;(3)、是否存在反比例函数上不同于点D的一点F,满足:为直角三角形, , 且 , 若存在,请直接写出满足以上条件时点D的横坐标,若不存在,请说明理由.
(1)、如图①,当点D为中点时,k的值为 , 点E的坐标为;(2)、如图②,当点D在线段上的任意位置时(不与重合),连接 , 求证:;(3)、是否存在反比例函数上不同于点D的一点F,满足:为直角三角形, , 且 , 若存在,请直接写出满足以上条件时点D的横坐标,若不存在,请说明理由.