北师大版数学九（上）期中题型汇编12 解答题—一元二次方程

试卷更新日期：2023-10-29 类型：复习试卷

进入出卷网下载

一、计算题

1. 解方程：

(1)、 $x^{2} - 3 x + 1 = 0$ ；

(2)、 $3 x (x - 2) = 2 (2 - x)$ ；

(3)、 $x^{2} + 4 x - 5 = 0$ ．

查看试题解析
2. 解一元二次方程.

(1)、 $x^{2} - 4 x - 7 = 0$

(2)、 $(2 x + 1)^{2} - 4 (2 x + 1) = 0$

查看试题解析
3. 用适当的方法解方程

(1)、 ${(2 x - 1)}^{2} = {(3 - x)}^{2}$

(2)、 $x^{2} - 4 x - 7 = 0$ （配方法）

(3)、 $x^{2} - 5 x - 6 = 0$

(4)、已知关于x的一元二次方程 $m x^{2} - (2 m - 1) x + m - 2 = 0$ 有两个不相等的实数根．求m的取值范围．

查看试题解析

二、解答题

4.

(1)、解方程： $x^{2} - 10 x + 9 = 0$ （配方法）；

(2)、解方程： $x (x - 2) = 5$ ；

(3)、关于x的一元二次方程 $a x^{2} - b x + 2 = 0 (a \neq 0)$ 有两个相等的实数根，请写出一组满足条件的a，b的值，并求出此时方程的根．

查看试题解析
5. 已知关于x的方程 $(k - 2) x^{2} - 2 x + 1 = 0$ 有两个实数根．

(1)、求k的取值范围；

(2)、当k取最大整数时，求此时方程的根．

查看试题解析
6. 已知方程 $2 x^{2} - k x - 6 = 0$ 的一个根为 $x_{1} = - 2$ .

(1)、求 $k$ 的值；

(2)、设方程的另一个根为 $x_{2}$ ，求 ${x_{1}}^{2} \cdot x_{2} + x_{1} \cdot {x_{2}}^{2}$ 的值.

查看试题解析
7. 疫情期间，学校利用一段长度仅为5米的围墙搭建一个矩形临时隔离点 $A B C D$ ，如图所示，它的另外三边所围的总长度是10米，矩形隔离点的面积为12平方米，求 $A B$ 的长度.

查看试题解析
8. 某中学有一块长 $30 m$ ，宽 $20 m$ 的矩形空地，计划在这块空地面积的一半区域种花，其余部分硬化.如图所示，小亮同学设计了一个宽度相同的“U”形区域，求花带的宽度.

查看试题解析
9. 光明中学准备在校园里利用围墙（墙长 $15 m$ ）和 $42 m$ 长的篱笆墙围建劳动实践基地．该校某数学兴趣小组设计了如下的围建方案（除围墙外，实线部分均为篱笆墙，且不浪费篱笆墙）：利用围墙和篱笆围成Ⅰ，Ⅱ两块矩形劳动实践基地，且在Ⅱ区中留一个宽度 $E H = 1 m$ 的水池．已知 $C G = 2 D G$ ，劳动基地的总面积（不包含水池）为 $100 m^{2}$ ，则 $D G$ 的长是多少？

查看试题解析
10. 西瓜经营户以2元/千克的价格购入一批小型西瓜，以3元/千克的价格出售，每天可以售出200千克，为了促销减少库存，该经营户决定降价销售，经调查发现，这种小型西瓜每降价0.1元/千克，每天可多售出40千克，该经销户想每天盈利224元，应将每千克小型西瓜的售价降多少元？

查看试题解析
11. 如图，在矩形ABCD中， $A B = 12 c m$ ， $B C = 6 c m$ ．点P沿AB边从点A开始向点B以2cm/s的速度移动，点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（s）表示移动的时间（0≤t≤6）．那么当t为何值时， $△ Q A P$ 的面积等于8 $c m^{2}$ ？

查看试题解析
12. 一道古算题：有执长竿入城门者，横执之多六尺，竖执之多三尺，有老父至，教他斜竿对两角，不多不少刚抵足，借问竿长多少数？
大意如下：某人拿着长竹竿进城门，横着拿竿多六尺，竖着拿竿多三尺，有一个经验丰富的老者，教他斜着拿竹竿进城门，竹竿刚好就是城门斜对角线的长度，正好可以进城，问竹竿长多少尺？（城门为矩形）

查看试题解析

三、综合题

13. 某公司设计了一款工艺品，每件的成本是40元，为了合理定价，投放市场进行试销：据市场调查，销售单价是50元时，每天的销售量是100件，而销售单价每提高1元，每天就减少售出2件，但要求销售单价不得超过65元．

(1)、若销售单价为每件52元，求每天的销售利润；

(2)、要使每天销售这种工艺品盈利1350元，那么每件工艺品售价应为多少元？

查看试题解析
14. 某单位准备举办羽毛球邀请赛，赛制为单循环（每两位选手之间各进行一场比赛），计划一共举行45场比赛.

(1)、求该邀请赛的参赛选手人数；

(2)、为了保证比赛正常进行，该单位需要为每场比赛至少准备4只羽毛球，且计划购买的羽毛球数量为10的整数倍.计划购买的某品牌羽毛球原价4元/只，现有甲，乙两家公司促销该品牌羽毛球.甲公司促销方案：在原价的基础上，在一定范围内每多购买10只，每个的单价可降低0.05元，例如购买20只时的单价为3.9元，最低单价不能低于2.8元；乙公司一律按8折促销.若该单位选择甲，乙中的一家公司购买，经过计算发现，分别选择在这两家公司购买的总金额相差40元，从节约成本的角度考虑，判断该单位应选择哪家公司购买，并求其计划购买的羽毛球数量.

查看试题解析
15. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = a$ ， $A C = b (a < b)$ ， $A B = 5$ ， $a$ ， $b$ 是方程 $x^{2} - (m - 1) x + (m + 4) = 0$ 的两根.

(1)、求 $a$ ， $b$ ；

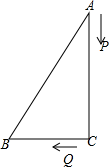(2)、 $P$ ， $Q$ 两点分别从 $A$ ， $C$ 出发，分别以每秒2个单位，1个单位的速度沿边 $A C$ ， $B C$ 向终点 $C$ ， $B$ 运动，（有一个点达到终点则停止运动），求经过多长时间后 $P Q = 2$ ？

查看试题解析
16. 芯片目前是全球紧缺资源，市政府通过资本招商引进“芯屏汽合、集终生智”等优势产业，发展新兴产业.某芯片公司，引进了一条内存芯片生产线，开工第一季度生产200万个，第三季度生产288万个.试回答下列问题：

(1)、已知每季度生产量的平均增长率相等，求前三季度生产量的平均增长率；

(2)、经调查发现，1条生产线最大产能是600万个/季度，若每增加1条生产线，每条生产线的最大产能将减少20万个/季度.现该公司要保证每季度生产内存芯片2600万个，在增加产能同时又要节省投入成本的条件下（生产线越多，投入成本越大），应该再增加几条生产线？

查看试题解析
17. 某水果商场经销一种高档水果，原价每千克50元．连续两次降价后每千克32元，若每次下降的百分率相同．

(1)、求每次下降的百分率；

(2)、若每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，商场决定采取适当的涨价措施，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，那么每千克应涨价多少元？

查看试题解析
18. 某大型电子商场销售某种空调，每台进货价为 $2500$ 元，标价为 $3200$ 元．

(1)、若电子商场连续两次降价，每次降价的百分率相同，最后以 $2592$ 元售出，求每次降价的百分率；

(2)、市场调研表明：当每台售价为 $3000$ 元时，平均每天能售出 $10$ 台，当每台售价每降 $100$ 元时，平均每天就能多售出4台，若商场要想使这种空调的销售利润平均每天达到 $5400$ 元，且顾客得到优惠，则每台空调应降价多少元？

查看试题解析
19. 某超市以每箱25元的进价购进一批水果，当该水果售价为40元/箱时，六月销售256箱，七、八月该水果十分畅销，销量持续上涨，在售价不变的基础上，八月的销量达到400箱．

(1)、求七，八两月的月平均增长率；

(2)、九月该超市为了减少库存，开始降价促销，经调查发现，该水果每箱降价1元，月销量在八月销量的基础上增加5箱，当该水果每箱降价多少元时，超市九月获利4250元？

查看试题解析
20. 某超市销售一种商品，成本价为50元/千克，规定每千克售价不低于成本价，且不高于85元．经市场调查，该商品每天的销售量y（千克）与售价x（元/千克）满足一次函数关系，如图所示：

(1)、求y与x之间的函数表达式；

(2)、该商场销售这种商品要想每天获得1350元的利润，每件商品的售价应定为多少元？

查看试题解析
21. 关于x的一元二次方程x²+mx+m-2＝0.

(1)、若-2是该方程的一个根，求该方程的另一个根；

(2)、求证：无论m取任何实数，此方程总有两个不相等的实数根；

(3)、设该方程的两个实数根为x₁ ， x₂ ，若x₁²+x₂²+m（x₁+x₂）＝m²+1，求m的值.

查看试题解析
22. “早黑宝”葡萄品种是我省农科院研制的优质新品种在我省被广泛种植，邓州市某葡萄种植基地2017年种植“早黑宝”100亩，到2019年“早黑宝”的种植面积达到196亩。

(1)、求该基地这两年“早黑宝”种植面积的平均增长率；

(2)、市场查发现，当“早黑宝”的售价为20元千克时，每天售出200千克，售价每降价1元，每天可多售出50千克，为了推广直传，基地决定降价促销，同时减存已知该基地“早黑宝”的平均成本价为12元/千克，若使销售“早黑宝”天获利1750元，则售价应降低多少元？

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 12 c m$ ， $B C = 24 c m$ ，动点 $P$ 从点 $A$ 开始沿边 $A B$ 向点 $B$ 以 $2 c m / s$ 的速度移动，动点 $Q$ 从点 $B$ 开始沿边 $B C$ 向点 $C$ 以 $4 c m / s$ 的速度移动，如果 $P$ ， $Q$ 两点分别从 $A$ ， $B$ 两点同时出发，设运动时间为 $x$ $s$ ．

(1)、用含x的式子表示：
$A P =$ $c m$ ，

$B P =$ $c m$ ，

$B Q =$ $c m$ ，

(2)、当 $△ P B Q$ 的面积为 $32 c m^{2}$ 时，求运动时间；

(3)、四边形 $A P Q C$ 的面积能否等于 $172 c m^{2}$ ？若能，求出运动的时间；若不能，说明理由．

查看试题解析
24. 暑假期间，某景区商店推出销售纪念品活动，已知纪念品每件的进货价为30元，经市场调研发现，当该纪念品的销售单价为40元时，每天可销售280件；当销售单价每增加1元时，每天的销售数量将减少10件（销售利润＝销售总额－进货成本）．设销售单价为x元（ $x > 40$ ）．

(1)、若该纪念品的销售单价为45元时，则当天销售量为多少件？

(2)、当该纪念品的销售单价为多少元时，该产品的当天销售利润是2610元？

(3)、该纪念品的当天销售利润有可能达到3700元吗？若能，请求出此时的销售单价；若不能，请说明理由．

查看试题解析
25. 如图为2022年10月的日历表，在其中用一个方框圈出4个数（如图中虚框所示），设这4个数从小到大依次为 $a$ ， $b$ ， $c$ ， $d$ ．

(1)、若用含有 $a$ 的式子分别表示出 $b$ ， $c$ ， $d$ ，其结果应为： $b =$ ； $c =$ ； $d =$ ；

(2)、按这种方法所圈出的四个数中， $a b$ 的最大值为；

(3)、嘉嘉说：“按这种方法可以圈出四个数，使得 $b c$ 的值为135．”
淇淇说：“按这种方法可以圈出四个数，使最小数 $a$ 与最大数 $d$ 的乘积 $a d$ 为84．”
请你运用一元二次方程的相关知识分别说明二人的说法是否符合题意．

查看试题解析