北师大版数学九(上)期中题型汇编11 解答题—特殊四边形
试卷更新日期:2023-10-29 类型:复习试卷
一、解答题
-
1. 如图,在矩形中,两条对角线与相交于点O, , 求与的长.
 2. 如图,在中, . 求证:是菱形.
2. 如图,在中, . 求证:是菱形. 3. 如图,在菱形中,点E是边上一点,延长至点F,使 , 连接 . 求证: .
3. 如图,在菱形中,点E是边上一点,延长至点F,使 , 连接 . 求证: . 4. 如图,在矩形中,点E,F分别在边上, , 且 , 与相交于点G.求证:矩形为正方形;
4. 如图,在矩形中,点E,F分别在边上, , 且 , 与相交于点G.求证:矩形为正方形; 5. 如图,矩形矩形 , 与相交于G,与相交于H. 请判断并证明四边形的形状.
5. 如图,矩形矩形 , 与相交于G,与相交于H. 请判断并证明四边形的形状. 6. 在中,E、F分别是边BC,AD的中点,AC是对角线,过点D作DPAC,交BA的延长线于点P,∠P=90°.求证:四边形AECF是菱形.
6. 在中,E、F分别是边BC,AD的中点,AC是对角线,过点D作DPAC,交BA的延长线于点P,∠P=90°.求证:四边形AECF是菱形. 7. 如图,是正方形的对角线上的两点,且 , 求证:;
7. 如图,是正方形的对角线上的两点,且 , 求证:;
二、综合题
-
8. 在菱形中,.(1)、以线段为边求作菱形;(要求:尺规作图,不写作法,保留作图痕迹)
 (2)、若菱形的面积为 , 求的长.9. 如图,矩形的顶点E,G分别在菱形的边 , 上,顶点F,H在菱形的对角线上.
(2)、若菱形的面积为 , 求的长.9. 如图,矩形的顶点E,G分别在菱形的边 , 上,顶点F,H在菱形的对角线上. (1)、求证:;(2)、若E为中点, , 求菱形的周长.10. 如图,P是正方形ABCD内一点,△ABP绕着点B旋转后能到达△CBE的位置.
(1)、求证:;(2)、若E为中点, , 求菱形的周长.10. 如图,P是正方形ABCD内一点,△ABP绕着点B旋转后能到达△CBE的位置. (1)、旋转的角度是多少度?(2)、若BP=3cm,求线段PE的长.11. 如图,已知在△OAB中AO=BO,分别延长AO,BO到点C、D,使得OC=AO,OD=BO,连接AD,DC,CB.
(1)、旋转的角度是多少度?(2)、若BP=3cm,求线段PE的长.11. 如图,已知在△OAB中AO=BO,分别延长AO,BO到点C、D,使得OC=AO,OD=BO,连接AD,DC,CB. (1)、求证:四边形ABCD是矩形;(2)、以AO,BO为一组邻边作平行四边形AOBE,连接CE.若CE⊥AE,求∠AOB的度数.12. 已知:如图,将绕点旋转一定角度得到 , 若 .
(1)、求证:四边形ABCD是矩形;(2)、以AO,BO为一组邻边作平行四边形AOBE,连接CE.若CE⊥AE,求∠AOB的度数.12. 已知:如图,将绕点旋转一定角度得到 , 若 . (1)、求证:;(2)、若 , , 求四边形的面积.13. 如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,过点B、点C分别作BE∥CD,CE∥BD.
(1)、求证:;(2)、若 , , 求四边形的面积.13. 如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,过点B、点C分别作BE∥CD,CE∥BD. (1)、求证:四边形BECD是菱形;(2)、若∠A=60°,AC= , 求菱形BECD的面积.14. 如图,为矩形对角线的中点,于点 , 交 , 于点 , , 连接 , .
(1)、求证:四边形BECD是菱形;(2)、若∠A=60°,AC= , 求菱形BECD的面积.14. 如图,为矩形对角线的中点,于点 , 交 , 于点 , , 连接 , . (1)、求证:四边形为菱形;(2)、若 , , 求的长.15. 如图,菱形的对角线与交于点O,分别过点C、点D作、的平行线交于点E,连接交于点F.
(1)、求证:四边形为菱形;(2)、若 , , 求的长.15. 如图,菱形的对角线与交于点O,分别过点C、点D作、的平行线交于点E,连接交于点F. (1)、求证:四边形是矩形;(2)、若 , , 求的长.16. 如图,在菱形ABCD中,对角线AC和BD交于点O,E为AB上一动点,过点E作EF∥BD交AD于点F,连接BF、DE.
(1)、求证:四边形是矩形;(2)、若 , , 求的长.16. 如图,在菱形ABCD中,对角线AC和BD交于点O,E为AB上一动点,过点E作EF∥BD交AD于点F,连接BF、DE. (1)、若∠ABD=40°,求∠CAD的度数;(2)、求证:BF=DE.17. 在菱形ABCD中,过点B作于点E,点F在边AB上,AF=CE,连接BD、DF.
(1)、若∠ABD=40°,求∠CAD的度数;(2)、求证:BF=DE.17. 在菱形ABCD中,过点B作于点E,点F在边AB上,AF=CE,连接BD、DF.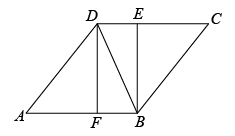 (1)、求证:四边形BFDE是矩形;(2)、若BD=2 , BE=4,求BC的长.18. 如图,将矩形绕着点按顺时针方向旋转得到矩形 , 使点落在边上的点处,连接交于点 , 连接 .
(1)、求证:四边形BFDE是矩形;(2)、若BD=2 , BE=4,求BC的长.18. 如图,将矩形绕着点按顺时针方向旋转得到矩形 , 使点落在边上的点处,连接交于点 , 连接 . (1)、求证:平分;(2)、取中点 , 连接 , 求证:;19. 如图,在中,相交于点O,E,F分别是的中点.
(1)、求证:平分;(2)、取中点 , 连接 , 求证:;19. 如图,在中,相交于点O,E,F分别是的中点. (1)、求证:;(2)、连接 , 已知(从以下两个条件中任选一个作为已知,填写序号),请判断四边形的形状,并证明你的结论.
(1)、求证:;(2)、连接 , 已知(从以下两个条件中任选一个作为已知,填写序号),请判断四边形的形状,并证明你的结论.条件①:;
条件②: .
(注:如果选择条件①条件②分别进行解容,按第一个解答计分)
20. 如图,将一张矩形的纸片沿向上折叠,顶点C落在点E处,交于F.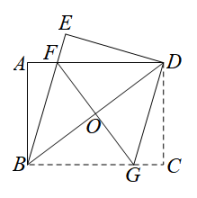 (1)、求证:是等腰三角形;(2)、过D作交于G,连接 , 交于O.
(1)、求证:是等腰三角形;(2)、过D作交于G,连接 , 交于O.①判断四边形的形状;
②若 , , 求的长.
21. 如图,点 , 分别在正方形的边 , 上,且 , 把绕点顺时针旋转得到 .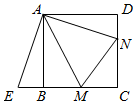 (1)、求证:≌ .(2)、若 , , 求正方形的边长.22. 在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点B逆时针旋转一个角度α后得到△DBE,点A,C的对应点分别为点D,E.
(1)、求证:≌ .(2)、若 , , 求正方形的边长.22. 在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点B逆时针旋转一个角度α后得到△DBE,点A,C的对应点分别为点D,E. (1)、如图1,若点D恰好落在边BC的延长线上,连接CE,求∠DEC的度数.(2)、如图2,若α=60°,F为BD的中点,连接CD,CF,EF,请判断四边形CDEF是什么特殊的四边形,并说明理由.23. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为 , D是的中点,点E在线段上.
(1)、如图1,若点D恰好落在边BC的延长线上,连接CE,求∠DEC的度数.(2)、如图2,若α=60°,F为BD的中点,连接CD,CF,EF,请判断四边形CDEF是什么特殊的四边形,并说明理由.23. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为 , D是的中点,点E在线段上. (1)、点D的坐标是;(2)、求直线CD的解析式;(3)、当的周长最小时,求点E的坐标.24. 如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E,使AE∥BC,连接AE.
(1)、点D的坐标是;(2)、求直线CD的解析式;(3)、当的周长最小时,求点E的坐标.24. 如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E,使AE∥BC,连接AE. (1)、求证:四边形ADCE是矩形;(2)、①若AB=17,BC=16,则四边形ADCE的面积=.
(1)、求证:四边形ADCE是矩形;(2)、①若AB=17,BC=16,则四边形ADCE的面积=.②若AB=10,则BC=时,四边形ADCE是正方形.
25. 如图,在平行四边形中,对角线 , 相交于点O,交的延长线于点E, . (1)、求证:四边形是矩形;(2)、若 , , 求矩形的面积.26. 如图,点是正方形的边上的一点,延长到使 , 连接、.
(1)、求证:四边形是矩形;(2)、若 , , 求矩形的面积.26. 如图,点是正方形的边上的一点,延长到使 , 连接、. (1)、能通过旋转得到吗?说明理由.(2)、连接 , 过作垂直于 , 交于 , 若 , , 求的长.27. 如图,在正方形ABCD中,E为CD边上一点,以DE为边向外作正方形DEFG,将正方形DEFG绕点D顺时针旋转,连接AG.
(1)、能通过旋转得到吗?说明理由.(2)、连接 , 过作垂直于 , 交于 , 若 , , 求的长.27. 如图,在正方形ABCD中,E为CD边上一点,以DE为边向外作正方形DEFG,将正方形DEFG绕点D顺时针旋转,连接AG. (1)、如图1,若AD=2、DE=2,当时,求AG的长;(2)、如图2,正方形DEFG绕点D旋转的过程中,取AG的中点M,连接DM、CE,猜想:DM和CE之间有何等量关系?并利用图2加以证明.28. 如图,正方形和正方形有公共点A,点B在线段上,
(1)、如图1,若AD=2、DE=2,当时,求AG的长;(2)、如图2,正方形DEFG绕点D旋转的过程中,取AG的中点M,连接DM、CE,猜想:DM和CE之间有何等量关系?并利用图2加以证明.28. 如图,正方形和正方形有公共点A,点B在线段上, (1)、求证:;(2)、判断与的位置关系,并说明理由.29. 将矩形纸片放在平面直角坐标系中,点 , 点 , 点 . 现绕点O顺时针旋转矩形纸片 , 得到新的矩形 , 其中A,B,C的对应点分别为 . 当直线与直线有交点时,设交点为D.
(1)、求证:;(2)、判断与的位置关系,并说明理由.29. 将矩形纸片放在平面直角坐标系中,点 , 点 , 点 . 现绕点O顺时针旋转矩形纸片 , 得到新的矩形 , 其中A,B,C的对应点分别为 . 当直线与直线有交点时,设交点为D. (1)、在旋转过程中,判断线段和的数量关系,并以图①为例说明理由;(2)、在旋转过程中,当点落在线段上时(如图②),直接写出点的坐标;(3)、在旋转过程中,若线段恰好过线段中点E时(如图③),求线段的长;(4)、在旋转过程中,当线段与线段的交点M恰好是线段中点时(如图④),请直接写出点M和点D的坐标.30. 正方形ABCD中,将边AB所在直线绕点A逆时针旋转一个角度a得到直线AM,过点C作CE⊥AM,垂足为E,连接BE.
(1)、在旋转过程中,判断线段和的数量关系,并以图①为例说明理由;(2)、在旋转过程中,当点落在线段上时(如图②),直接写出点的坐标;(3)、在旋转过程中,若线段恰好过线段中点E时(如图③),求线段的长;(4)、在旋转过程中,当线段与线段的交点M恰好是线段中点时(如图④),请直接写出点M和点D的坐标.30. 正方形ABCD中,将边AB所在直线绕点A逆时针旋转一个角度a得到直线AM,过点C作CE⊥AM,垂足为E,连接BE. (1)、当0°<a<45°时,设AM交BC于点F,
(1)、当0°<a<45°时,设AM交BC于点F,①如图1,若a=35°,求∠BCE的度数;
②如图2,用等式表示线段AE,BE,CE之间的数量关系,并证明;
(2)、当45°<a<90°时(如图3),请直接用等式表示线段AE,BE,CE之间的数量关系。