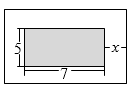
北师大版数学九(上)期中题型汇编2 选择题—一元二次方程
试卷更新日期:2023-10-29 类型:复习试卷
一、选择题
-
1. 已知关于x的方程:(1)ax2+bx+c=0;(2)x2-4x=8+x2;(3)1+(x-1)(x+1)=0;(4)(k2+1)x2+kx+1=0中,一元二次方程的个数为( )A、1 B、2 C、3 D、42. 用配方法解一元二次方程 , 下列配方正确的是( )A、 B、 C、 D、3. 把方程x2﹣8x+3=0化成(x﹣m)2=n的形式,则m、n的值是( )A、﹣4,13 B、﹣4,19 C、4,13 D、4,194. 一元二次方程 , 下列分解正确的是( )A、 B、 C、 D、5. 若a,b,c是△ABC的三边长,则关于x的方程的根的情况是( )A、无实数根 B、有两相等的实数根 C、有两不相等的实数根 D、无法确定6. 已知和是一元二次方程的实数根,则的值为( )A、2 B、 C、1 D、7. 若关于x的一元二次方程kx2-2x-1=0有两个实数根,则k的取值范围是( )A、k≠0 B、k≥-1 C、k≥-1且k≠0 D、k>-1且k≠08. 关于一元二次方程(k为常数)的根的情况,下列说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定根的情况9. 已知关于x的一元二次方程 , 若等腰三角形的其中一边为4,另两边是这个方程的两根,则m的值为( )A、3 B、4 C、3或4 D、不能确定10. 如果m、n是一元二次方程x2+x=4的两个实数根,那么多项式2n2-mn-2m的值是( )A、16 B、14 C、10 D、611. 已知方程 , 等号右侧的数字印刷不清楚,若可以将其配方成的形式,则印刷不清楚的数字是( )A、6 B、9 C、2 D、-212. 若关于x的方程(m-3)x|m-1|+5x-3=0是一元二次方程,则m的值为( )A、3 B、-1 C、3或-1 D、013. 将下列一元二次方程化成一般形式后,其中二次项系数是4,一次项系数是-7,常数项是2的方程是( )A、 B、 C、 D、14. 若关于x的一元二次方程有两个相等的实数根,则a的取值为( )A、 B、 C、 D、15. 若关于x的一元二次方程有两个实数根,则k的取值范围是( )A、 B、 C、且 D、且16. 若关于的一元二次方程有两个不相等的实数根,则一次函数的图象可能是( )A、
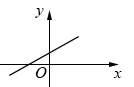 B、
B、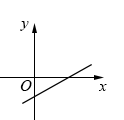 C、
C、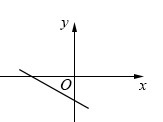 D、
D、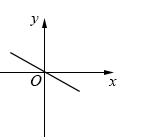 17. 对于一元二次方程(a≠0),下列命题中错误的是( )A、a+b+c=0,则 B、若方程有两个不相等的实根,则方程必有两个不相等的实根 C、若c是方程的一个根,则一定有ac+b+1=0成立 D、若x0是一元二次方程的根,则18. 有一个两位数,个位数字与十位数字之和为8,把它的个位数字与十位数字对调,得到一个新数,新数与原数之积为1855,则原两位数是( )A、35 B、53 C、62 D、35或5319. 若一元二次方程有两个不相等的实数根 , 且 , 则的值是( )A、-1 B、3 C、2或-1 D、-3或120. 在二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表,则方程ax2+bx+c=0的一个解x的范围是( )
17. 对于一元二次方程(a≠0),下列命题中错误的是( )A、a+b+c=0,则 B、若方程有两个不相等的实根,则方程必有两个不相等的实根 C、若c是方程的一个根,则一定有ac+b+1=0成立 D、若x0是一元二次方程的根,则18. 有一个两位数,个位数字与十位数字之和为8,把它的个位数字与十位数字对调,得到一个新数,新数与原数之积为1855,则原两位数是( )A、35 B、53 C、62 D、35或5319. 若一元二次方程有两个不相等的实数根 , 且 , 则的值是( )A、-1 B、3 C、2或-1 D、-3或120. 在二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表,则方程ax2+bx+c=0的一个解x的范围是( )x
…
1
1.1
1.2
1.3
1.4
…
y
…
1
0.49
0.04
0.59
1.16
…
A、1<x<1.1 B、1.1<x<1.2 C、1.2<x<1.3 D、1.3<x<1.421. 使得关于x的不等式组有且只有4个整数解,且关于x的一元二次方程有实数根的所有整数a的值之和为( )A、35 B、30 C、26 D、2122. 关于x的一元二次方程的两实数根 , 则的值是( )A、8 B、32 C、8或32 D、16或4023. 若m、n是关于x的方程的两个根,则的值为( )A、 B、 C、 D、24. 对于实数a,b定义运算“”为 , 例如 , 则关于x的方程的根的情况,下列说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定25. 一个三角形的两边长为3和6,第三边边长是方程(x-2)(x-4)=0的根,则这个三角形的周长为 ( )A、11 B、13 C、11或13 D、11和1326. 新能源汽车节能、环保,越来越受消费者喜爱,各种品牌的新能源汽车相继投放市场,我国新能源汽车近几年销售量全球第一,2020年某款新能源车销售量为19万辆,销售量逐年增加,到2022年销售量为25.6万辆,求这款新能源汽车的年平均增长率是多少?可设年平均增长率为x,根据题意可列方程为:( )A、19 (1+ x)2= 25.6 B、19(3+x)2=25.6 C、19(1+2x)2=25.6 D、19+19(1+x)+19(1+ x) 2=25.627. 某县为发展教育事业,加强了对教育经费的投入,2020年投入3000万元,预计2022年投入5000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )A、 B、 C、 D、28. 2022年北京冬奥会女子冰壶比赛,有若干支队伍参加了单循环比赛(每两队之间都赛一场),单循环比赛共进行了45场,共有多少支队伍参加比赛?设共有x支队伍参加比赛,则所列方程为( )A、x(x+1)=45 B、=45 C、x(x-1)=45 D、=45